Judgments, conclusions, syllogisms ... or the achievement of ancient logic in one post
When I was in school, we studied logic, but now, for some reason, they don’t teach it even in my beloved lyceum. Moreover, I learned that most of my friends (even those who have successfully graduated from high schools) do not know either about the logical square or about the various modes. In this small topic, I will try to briefly talk about everything. I must say right away that the gurus of discrete mathematics are unlikely to learn something new, but the rest should be at least interesting, and at most useful.
Let's start with the basics. Those. with judgments. If you do not introduce strict definitions, then in judgments simply something is affirmed or denied. In the vast majority of languages, judgments are constructed according to the following form: S is P, while S is called the subject of judgment, and P is a predicate.
Judgments can be divided according to many criteria. For example, simple (judgments without logical connectives) and complex. In this case, simple judgments can be divided into attributive (affirm or deny the existence of the attribute), existential (affirm or deny the existence of something) and judgments with relationships. Another version of the classification of judgments is the classification by quality: statements are divided into affirmative and negative. The most interesting classification for us is the classification by quantity. We will consider it in more detail.
• General affirmative statements of the form “all S are P” are called type A propositions.
• Partially affirmative statements of the form “some S are P” are called type I propositions.
• Generally negative judgments of the type “no S are P” are called type E propositions.
• Partially negative judgments of the form “some S is not P” are called propositions of type O.
The tradition to designate judgments with the letters AIEO originated in the Middle Ages. These vowels are taken from the Latin words affirmo (affirm) and nego (deny).
Classification of judgments by quantity is important, because on its basis the famous logical square was built.
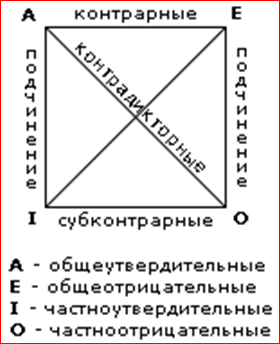
In the corners of the square, the types of judgments are shown, and on the sides and diagonals of the square the relationships between the respective judgments are indicated. These relationships require some explanation.
If between judgments the relation of submission acts , then the following can be said about their truth. If the general judgment is true, then subordinate judgments are also true. If the general judgment is false, then nothing definite can be said about a particular judgment. If a particular judgment is true, then nothing definite can be said about the general. If a particular judgment is false, then a general judgment is also false.
Counterjudgments may be false at the same time, but they cannot be true at the same time.
Subcontrol judgments can be true at the same time, but they cannot be false at the same time.
Contradictory judgments cannot be either true or false at the same time. Those. if one of the counter-judgments is true, then the second is necessarily false and vice versa.
Having dealt with judgments, we can move on to the rules for obtaining new judgments, i.e. inferences. Let's start with the simplest direct conclusions.
A new judgment is obtained by changing the quality of the package. For this, it is necessary to insert two negatives into the original proposition: before the connective and before the predicate. In fact, this is a very simple conclusion, in fact, it boils down to the following transformations of AE, EA, IO, OI.
Those. the judgment “some people are talented” after the transformation becomes the proposition “some people are not talented” (OI).
In circulation, a new conclusion is obtained after rearrangement of the subject and predicate in places. Those. the proposition “S is P” turns into the proposition “P is S”. Unfortunately, it is impossible to apply this operation to any statements, otherwise from the statement “cats are mammals” we would get “mammals are cats”.
In order for the appeal to be true, it is necessary to observe the following rules:
• General affirmative judgments turn into private affirmative
• General negative judgments turn into general negative judgments
• Private affirmative judgments turn into private affirmative judgments
• Partially negative judgments do not appeal at all
This is the most difficult operation, which is essentially a combination of transformation and conversion. In practice, it looks like this: “S is P” turns into “not P is not S”. I will not specifically cite the restrictions imposed on opposing the predicate here, so you yourself can think a little.
In the meantime, we will begin to consider syllogisms. Syllogisms are the most popular type of proposition, it includes three propositions (two premises and conclusion) and three terms.
The smaller term (S) is the subject of the judgment that came out as a conclusion. The larger term (P) is a predicate of inference. The middle term (M) is included in both premises, but not in the output.
For a syllogism to be correct, it must obey three groups of rules: rules of terms, rules of premises, rules of figures.
• There should be exactly 3 terms in a syllogism.
• The average term must be taken in full in at least one of the premises.
• If the term is not taken in full in the package, then it cannot be taken in full and in the conclusion.
To understand the importance of these rules, I will give just one example: “Some living things are poisonous. Seals are living things. Seals are poisonous. ” Which of the rules is broken, try to determine for yourself.
• No conclusion follows from two negative premises.
• If one premise is negative, then the conclusion must be negative.
• From two private premises no conclusion follows.
Do you remember that there are three judgments and three terms in a syllogism? According to the mutual arrangement of terms in judgments, syllogisms can be divided into 4 classes (figures):

Rules of figures:
• For the first figure, the first premise should be a general proposition, and the smaller assertive
• For the second figure, a larger premise should be a general proposition, and a smaller premise and conclusion negative.
• In the third figure, the smaller premise must be an affirmative judgment, and the conclusion is private.
• The fourth premise is least likely to occur, it has two whole rules: 1. if the general premise is an affirmative proposition, then the smaller premise should be a general proposition; 2. If one of the premises is negative, then the large package should be common.
Again, violation of the rules of the figures leads to very funny logical errors: “All cats drink water. I drink water. I’m a cat. "
In fact, syllogisms can be divided not only by the mutual arrangement of S, P, M, but also by the types of judgments (A, I, O, E) included in the syllogism. It is easy to see that a total of 64 different syllogisms are possible; these syllogisms are called modes. If we apply to the mods all the restrictions and rules that we talked about, it turns out that there are only 19 logically correct mods and they are distributed according to the figures as follows:

If you know these rules and use them, you can, firstly, avoid stupid mistakes, and secondly, notice these mistakes in your opponents in disputes.
In fact, what is described in the post is only a small part of the achievements of ancient thinkers. We didn’t talk at all about entimems, nor about epheirams, nor about categorical-categorical syllogisms, nor about ... Yes, we almost did not talk about anything, but I still hope that it was interesting to you.
Judgments
Let's start with the basics. Those. with judgments. If you do not introduce strict definitions, then in judgments simply something is affirmed or denied. In the vast majority of languages, judgments are constructed according to the following form: S is P, while S is called the subject of judgment, and P is a predicate.
Judgments can be divided according to many criteria. For example, simple (judgments without logical connectives) and complex. In this case, simple judgments can be divided into attributive (affirm or deny the existence of the attribute), existential (affirm or deny the existence of something) and judgments with relationships. Another version of the classification of judgments is the classification by quality: statements are divided into affirmative and negative. The most interesting classification for us is the classification by quantity. We will consider it in more detail.
• General affirmative statements of the form “all S are P” are called type A propositions.
• Partially affirmative statements of the form “some S are P” are called type I propositions.
• Generally negative judgments of the type “no S are P” are called type E propositions.
• Partially negative judgments of the form “some S is not P” are called propositions of type O.
The tradition to designate judgments with the letters AIEO originated in the Middle Ages. These vowels are taken from the Latin words affirmo (affirm) and nego (deny).
Logical square
Classification of judgments by quantity is important, because on its basis the famous logical square was built.

In the corners of the square, the types of judgments are shown, and on the sides and diagonals of the square the relationships between the respective judgments are indicated. These relationships require some explanation.
If between judgments the relation of submission acts , then the following can be said about their truth. If the general judgment is true, then subordinate judgments are also true. If the general judgment is false, then nothing definite can be said about a particular judgment. If a particular judgment is true, then nothing definite can be said about the general. If a particular judgment is false, then a general judgment is also false.
Counterjudgments may be false at the same time, but they cannot be true at the same time.
Subcontrol judgments can be true at the same time, but they cannot be false at the same time.
Contradictory judgments cannot be either true or false at the same time. Those. if one of the counter-judgments is true, then the second is necessarily false and vice versa.
Inferences
Having dealt with judgments, we can move on to the rules for obtaining new judgments, i.e. inferences. Let's start with the simplest direct conclusions.
Simple conclusions
Turning
A new judgment is obtained by changing the quality of the package. For this, it is necessary to insert two negatives into the original proposition: before the connective and before the predicate. In fact, this is a very simple conclusion, in fact, it boils down to the following transformations of AE, EA, IO, OI.
Those. the judgment “some people are talented” after the transformation becomes the proposition “some people are not talented” (OI).
Appeal
In circulation, a new conclusion is obtained after rearrangement of the subject and predicate in places. Those. the proposition “S is P” turns into the proposition “P is S”. Unfortunately, it is impossible to apply this operation to any statements, otherwise from the statement “cats are mammals” we would get “mammals are cats”.
In order for the appeal to be true, it is necessary to observe the following rules:
• General affirmative judgments turn into private affirmative
• General negative judgments turn into general negative judgments
• Private affirmative judgments turn into private affirmative judgments
• Partially negative judgments do not appeal at all
Predicate Opposition
This is the most difficult operation, which is essentially a combination of transformation and conversion. In practice, it looks like this: “S is P” turns into “not P is not S”. I will not specifically cite the restrictions imposed on opposing the predicate here, so you yourself can think a little.
Syllogisms
In the meantime, we will begin to consider syllogisms. Syllogisms are the most popular type of proposition, it includes three propositions (two premises and conclusion) and three terms.
The smaller term (S) is the subject of the judgment that came out as a conclusion. The larger term (P) is a predicate of inference. The middle term (M) is included in both premises, but not in the output.
For a syllogism to be correct, it must obey three groups of rules: rules of terms, rules of premises, rules of figures.
Terms Rules
• There should be exactly 3 terms in a syllogism.
• The average term must be taken in full in at least one of the premises.
• If the term is not taken in full in the package, then it cannot be taken in full and in the conclusion.
To understand the importance of these rules, I will give just one example: “Some living things are poisonous. Seals are living things. Seals are poisonous. ” Which of the rules is broken, try to determine for yourself.
Parcel Rules
• No conclusion follows from two negative premises.
• If one premise is negative, then the conclusion must be negative.
• From two private premises no conclusion follows.
Rules of figures
Do you remember that there are three judgments and three terms in a syllogism? According to the mutual arrangement of terms in judgments, syllogisms can be divided into 4 classes (figures):

Rules of figures:
• For the first figure, the first premise should be a general proposition, and the smaller assertive
• For the second figure, a larger premise should be a general proposition, and a smaller premise and conclusion negative.
• In the third figure, the smaller premise must be an affirmative judgment, and the conclusion is private.
• The fourth premise is least likely to occur, it has two whole rules: 1. if the general premise is an affirmative proposition, then the smaller premise should be a general proposition; 2. If one of the premises is negative, then the large package should be common.
Again, violation of the rules of the figures leads to very funny logical errors: “All cats drink water. I drink water. I’m a cat. "
In fact, syllogisms can be divided not only by the mutual arrangement of S, P, M, but also by the types of judgments (A, I, O, E) included in the syllogism. It is easy to see that a total of 64 different syllogisms are possible; these syllogisms are called modes. If we apply to the mods all the restrictions and rules that we talked about, it turns out that there are only 19 logically correct mods and they are distributed according to the figures as follows:

If you know these rules and use them, you can, firstly, avoid stupid mistakes, and secondly, notice these mistakes in your opponents in disputes.
In fact, what is described in the post is only a small part of the achievements of ancient thinkers. We didn’t talk at all about entimems, nor about epheirams, nor about categorical-categorical syllogisms, nor about ... Yes, we almost did not talk about anything, but I still hope that it was interesting to you.
