Automatic column width calculation

Task

The task sounds simple - print a table. Print so that it looks beautiful and, if possible, does not crawl.

After some deliberation, it was decided to use FOP to generate the PDF. The catch is that Apache FOP does not support table-layout:auto, that is, when building a table, you must manually set the column width (it’s good that you can set the relative width in percent). If you make all the columns of the same width, the table will look somewhat inelegant. It turns out that you have to calculate the width manually.

The main idea is that the width of the columns must be selected in such a way as to reduce the number of line breaks inside the table cells as much as possible.

Decision

I solved the problem in C ++ using the Qt framework, so there will definitely be some references to the language and Qt, but in general, I will try to avoid the code and describe the main idea of ​​the solution.

Data preparation

First, decide what data is required. We divide the text in each cell of the table into words, for each word we calculate how much space it takes on paper. Thus, for each cell we will store an array of word lengths of its text.

In addition, you must know the width of the paper, and expressed in the same units as the length of words.

I used QFontMetrics :: width to determine the length of words. Thus, the length of words was obtained in pixels. Then, in order to determine the width of the paper in pixels, it is enough to multiply its width in inches by the DPI of the screen, which can be obtained using the QPaintDevice :: logicalDpiX function .


It may turn out that the width of the paper is not enough to fit the table, even if you squeeze the columns so that each row will fit just one word.

The likelihood of such a scenario is small (unless you are German and not a tester, of course), so I did not develop any complicated algorithm for handling such cases. Just check that the minimum width of the table, which is defined as the sum of the maximum word lengths in the columns, is smaller than the paper size.

minimum table width

determined by the sum of the lengths of the longest words in the columns

If the table does not fit, you will have to trim the long words. Since, since we decided to trim the word, we can trim it anywhere, we will consider the effective length of such cropped words to be zero.

So, we will trim the longest word in the table until the table begins to fit on paper.

On this, the data preparation can be considered complete, and we can proceed to the algorithm for calculating the width of the columns.

Payment

At the beginning of the article, I determined the main idea of ​​the solution. Now it is time to express it more formally. In fact, it is necessary to display the table on paper in such a way as to reduce the area of ​​the table as much as possible.
The area occupied by the table can be defined as the sum of the areas of its columns:

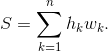
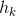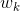Here and are the height and width of the column, respectively.

Of course, this is not entirely true, but such a model in practice gives a completely satisfactory result.

Let us write down what the column height is:

where m is the number of rows in the table, lh is the height of the line of text, p is some coefficient describing the height of the indentation, wc is the number of line breaks.

Since the number of rows, the row height, and padding affect not possible, they can be taken to a separate factor A .

But the number of line breaks depends on the width of the column. Thus, the column height can be rewritten in the form:


A task is reduced to minimizing the function


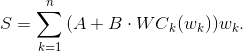
Yes, yes, I was not mistaken, A and B will not depend on k , since B is determined by the height of the line, and A , in addition, by the size of the indentation and the number of lines .

S can be rewritten as:


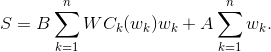
Now I will do a lot of rudeness. 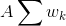Is the ideal area of ​​the table when there are no hyphens at all. But since we are not interested in optimizing for the width of the table, (in the end, we’ll still stretch the table to the entire page), then replace it , that is, with a constant. Now everything is simple: for the minimization problem, the coefficients G and B do not play any role, so you can safely throw them out and find the minimum of the function.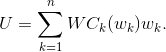


To find the minimum of the function, we will take the gradient descent method as the basis , but we will go down not in the direction of the gradient, but along that coordinate, the change functions (partial derivative multiplied by the change in coordinate) along which it has the smallest (it is also the largest in absolute value) value .

Did you say derivative?

In fact, the function of the number of transfers, depending on the width of the column, is not very smooth. This is a step function that suffers discontinuities at the points of change in the number of transfers. It looks something like this:

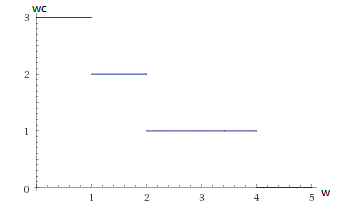
Such a function has obvious problems with derivatives, but we will do it simply: we will consider not the function itself, but some monotonically decreasing function, which at the points of change in the number of transfers coincides with the right limit of the original function.

As the starting point, take the point with the smallest possible column widths.

Algorithm

For each column:

• We construct arrays of points at which the number of hyphenations in this column changes - m _k .
• The arrays of values ​​of the smooth function of the number of transfers at these points (I defined the smooth function in the previous section) - wc _k .

In order to form these arrays, we use the data on the word length in each cell of the table prepared at the first stage.

We supplement the arrays (they turned out as many as the columns) with starting points.

As a result, for the column

minimum table width

we get the following data structure:

m 0	wc 0
eleven	2
13 (“width” and “tables” - on one line)	1
24	0

We obtain similar structures for the remaining columns.

Now start the iterative process:
So far, the sum of the column widths is less than the page width:

• We calculate the change in the area function ( U ) when moving along each coordinate according to the formula
  
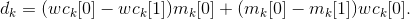
  (This is a well-known formula for taking the product differential: d (AB) = B d A + A d B)
• If in one array there is only one element left, then this column already has no line breaks ( wc _k [0] == 0 ). We do not take such a column into consideration.
• If not a single array has been considered, row breaks are already missing in all columns, we finish the calculations.
• Increase the width of the k- th column, in which d _k is the largest. We remove the first elements of the wc _k and m _k arrays for this column.

In conclusion, we recalculate the obtained column widths from absolute units to percent. Thus, we get rid of the font metric that we used.

Total

As a result, the table is exactly what I would do with manual formatting.

PS The
article does not pretend to be mathematically rigorous, but it shows where a little mathematics can be useful to you in applied programming.