Transparency versus surface orientation
The other day, turning a plastic cup in my hands, I noticed that the visible transparency of the plastic depends on the angle at which you look at the surface - if you look perpendicular to the surface, the background is clearly visible, and if you look along the surface, the material becomes almost opaque. This phenomenon interested me, and I decided to build a mathematical model.
No sooner said than done. Under the cutout, the formula output, fragment shader code and a small demo.
We assume that the material is optical homogeneous - its optical properties are independent of direction. Then the change in transparency is caused by different path lengths of the light beam in the thickness of the material.
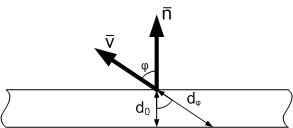
 , where
, where  is the unit normal vector to the surface,
is the unit normal vector to the surface,  is the unit direction vector to the observer.
is the unit direction vector to the observer.
Let the apparent transparency of the material be determined by the opacity coefficient, which determines the mixing of the color of the material with the background color as follows:C_\texttt{background})
Let's see how the value depends on the thickness of the material. To do this, we break the material layer with a thickness
depends on the thickness of the material. To do this, we break the material layer with a thickness  and opacity coefficient
and opacity coefficient  into
into  layers of the same thickness
layers of the same thickness  , each with an opacity coefficient
, each with an opacity coefficient  . Let
. Let  is the background color,
is the background color,  is the color of the material, and
is the color of the material, and  is the color at the output of each layer.
is the color at the output of each layer.
C_0&space;\par&space;C_2=\alpha_\varepsilon&space;C_m+(1-\alpha_\varepsilon)C_1&space;=&space;\alpha_\varepsilon&space;C_m+(1-\alpha_\varepsilon)[\alpha_\varepsilon&space;C_m+(1-\alpha_\varepsilon)C_0]&space;=&space;\par&space;=&space;(2\alpha_\varepsilon&space;-&space;\alpha_\varepsilon^2)C_m&space;+&space;(1-\alpha_\varepsilon)^2&space;C_0&space;=&space;(1-(1&space;-&space;\alpha_\varepsilon)^2)&space;C_m+(1-\alpha_\varepsilon)^2&space;C_0&space;\par&space;C_3=\alpha_\varepsilon&space;C_m+(1-\alpha_\varepsilon)C_2&space;=&space;\alpha_\varepsilon&space;C_m+(1-\alpha_\varepsilon)[(1-(1&space;-&space;\alpha_\varepsilon)^2)&space;C_m+(1-\alpha_\varepsilon)^2&space;C_0]&space;=&space;\par&space;=&space;(\alpha_\varepsilon&space;+&space;1&space;-&space;\alpha_\varepsilon&space;+&space;(1&space;-&space;\alpha_\varepsilon)^3)C_m&space;+&space;(1-\alpha_\varepsilon)^3&space;C_0&space;=&space;(1-(1&space;-&space;\alpha_\varepsilon)^3)&space;C_m+(1-\alpha_\varepsilon)^3&space;C_0&space;\par&space;...&space;\par&space;C_N=&space;(1-(1&space;-&space;\alpha_\varepsilon)^N)&space;C_m+(1-\alpha_\varepsilon)^N&space;C_0)
But alsoC_0) , and hence:
, and hence:

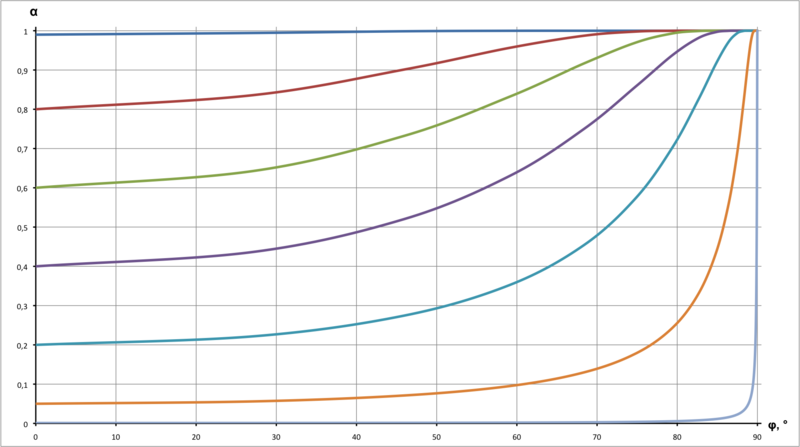
Ie with increasing thickness, the apparent transparency of the material decreases exponentially.
Let the thickness , then:
, then:
^k=(1-\alpha_\varepsilon)^\frac{d_\varphi}{d_\varepsilon}=(1-\alpha_0)^{\frac{d_\varepsilon}{d}\times&space;\frac{d_\varphi}{d_\varepsilon}}=(1-\alpha_0)^\frac{d_\varphi}{d_0}=(1-\alpha_0)^\frac{1}{\cos&space;\varphi})
So, the desired formula:&space;=&space;1&space;-&space;(1&space;-&space;\alpha_0)^\frac{1}{\cos&space;\varphi}})
The following is the fragment shader code that implements this formula:
The result is this:
Demo source code available at bitbucket.org
No sooner said than done. Under the cutout, the formula output, fragment shader code and a small demo.
We assume that the material is optical homogeneous - its optical properties are independent of direction. Then the change in transparency is caused by different path lengths of the light beam in the thickness of the material.

Let the apparent transparency of the material be determined by the opacity coefficient, which determines the mixing of the color of the material with the background color as follows:
Let's see how the value
But also

Ie with increasing thickness, the apparent transparency of the material decreases exponentially.
Let the thickness
So, the desired formula:

The following is the fragment shader code that implements this formula:
varying vec4 v_color;
varying vec3 v_normal;
varying vec3 v_eye;
void main(void)
{
// Вектора нормали и направления на наблюдателя не нормализированы
float cosPhi = dot(v_normal, v_eye) / sqrt( dot(v_normal, v_normal) * dot(v_eye, v_eye) );
// Косинус берется по модулю, на случай если наблюдатель находится сзади поверхности
// Чтобы избежать деления на нуль, значение косинуса принудительно ограничено снизу
// 0.999 ^ 10000 = 4.5173346E-5
float alpha = 1.0 - pow(1.0 - v_color.a, 1.0 / max(abs(cosPhi), 0.00001));
gl_FragColor = vec4(vec3(v_color), alpha);
};
The result is this:
Demo source code available at bitbucket.org
