Civilization Springs, 2/5

Part 2. Very Heavy Fuel

Previous part 1



Before you - the International Space Station. Weight of 420 tons and a value ^{[ 20 ]} to $ 150 billion count:



Its kinetic energy, good old E = mv ² /2, is 1.3 x 10 ¹³ joules. Adding potential energy at an altitude of 400 kilometers, we get 1.4 * 10 ¹³ J.

How much gasoline should be burned to get this energy? It turns out not so much. 350 tons in total. This is approximately ^{[ 200 ]} one-day energy budget of Ulan-Ude.

How is it that far from being the richest city in the world, in one single day, it manages enough energy to accelerate the ISS to orbital speed; however, we have one station for the whole world, and it costs indecently big money?

The answer lies in the obvious from the anatomy of the launch vehicle.

The carrier, as a minimum, is obliged to include:

1. Payload. Otherwise, why is it even needed?
2. At least one engine.
3. The body, all this connecting.
4. And, of course, fuel. As a working body and, in most cases, as a source of energy.

And at the last point, the problem is rooted. To raise and steal a certain minimum of fuel, you need ... right, extra fuel! On the rise of which you also need fuel! And this cheating continues for a long time. Of course, it converges, otherwise we would not fly anywhere at all. But according to the results of convergence, a modern rocket, even a multistage one, even qualitatively designed and executed, consists mainly of this very fuel.

Well, a textbook example, Saturn V is not the newest, but one of the most effective missiles in history ^{[ 30 ]} :



[Original image from NASA History [ 40 ]]

Starting weight - 2970 tons. About 2670 of them are fuel. Of which 2160 burn out in less than three minutes of the entire lunar expedition. Given that the kinetic energy of the payload in orbit is "worth" only about 100 tons of fuel.

It turns out that the main difficulty in entering orbit is not a lack of energy. Her earthlings are in abundance enough for the kinetic energy of not only stations, but at least cruise ships in orbit. The problem is different: our fuel is too heavy. Too much of it is needed in kilograms to collect the amount of energy required for flight. Why is used on most of the fuel poured into the rocket goes into transportation fuel also. Actually, the Tsiolkovsky formula, linking the starting M and the final mass of the rocket m with the typed speedV and the exhaust flow rate of the engine u , tells us the same thing:

M / m = e ^{V / u}     [2]

At first glance, it is not quite clear what is the content of energy per kilogram? But it's simple. It "sits" in u , at the rate of flow. For a chemical fuel, it is limited to (and in the first approximation it is equal to) u = √ (2 q ), where q is the specific heat of combustion. Which is the energy content per kilogram. And when this q "does not reach", the mass ratio at the start and finish turns out to be exponentially huge:

M / m = e^{V / √ (2 q )}     [3]

Or

V = Ln ( M / m ) * √ ( 2q ) [3a]


^{Article written for the site https://habr.com . When copying please refer to the source. The author of the article is Evgeny Bobukh .}

So, the rockets are expensive because their extremely lightweight “dry” construction is forced to withstand extremely heavy loads, mainly fuels (and even quickly “pump” it through the THA). And the load is great because our fuel is too heavy about . Very little in it is placed joules per kilogram.

Let us now understand the reasons for this restriction.

For which we take a closer look at the reaction of hydrogen burning in fluorine, as one of the simplest. In it, hydrogen-hydrogen and fluoride-fluorine pairs exchange partners, creating two hydrogen-fluorine pairs:

H ₂ + F ₂= 2 HF

Where does the released energy come from?

A hydrogen molecule has two atoms. The atoms have electrons. They are “smeared” around the atom in the form of such a cloud, and are connected with the nucleus mainly by electrostatic attraction. Electrons are external, valent, and (except hydrogen) internal, not participating in chemical reactions. After the reaction, hydrogen and fluorine are swapped. The electric clouds of valence electrons are redistributed and slightly change their shape. Something like this:



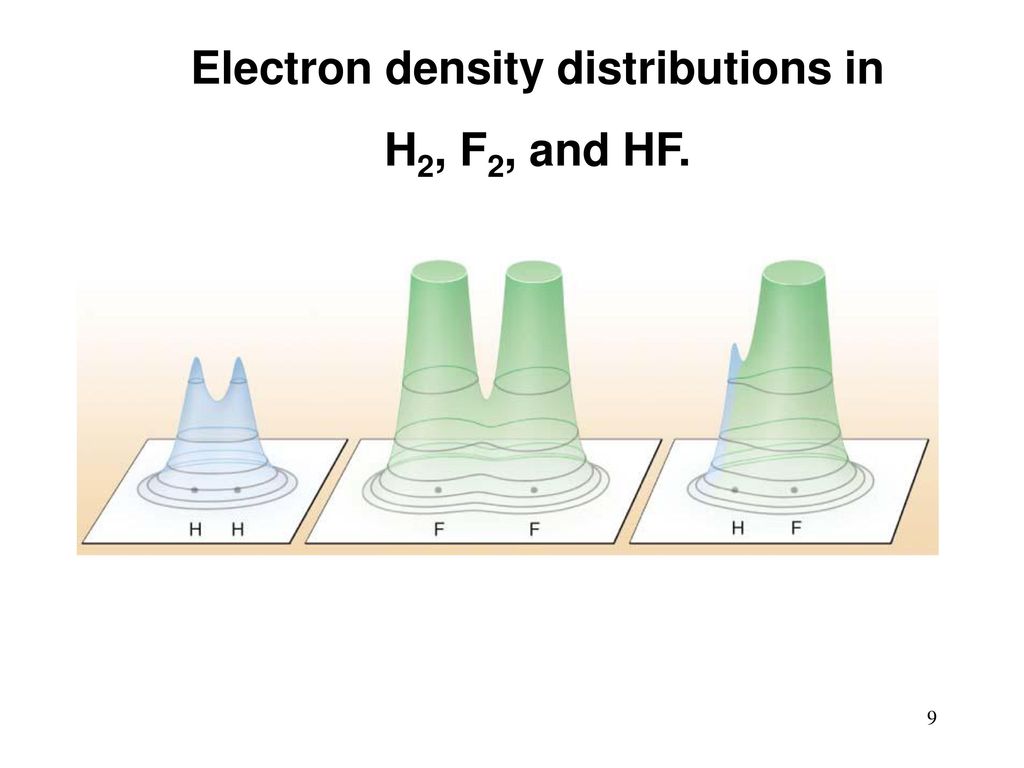
[Image credit [ 295 ]]

The potential energy of binding electrons to atoms in new clouds is different. In this case (this energy is negative) it is now less than that of H ₂ and F ₂separately. Where did the difference go? In the kinetic energy of a molecule, the vibrations of its atoms, electromagnetic radiation. All this eventually turned into heat. Which expanded gas and gave cravings.

And here is the crucial moment. Only external, valence electrons are involved in chemical reactions. The density distribution of other electrons (as well as the intensity of the electric field "in depth" of the atom) remain almost unchanged. In chemical reactions, atoms interact with each other as if through "intermediaries", which are the valence electrons:



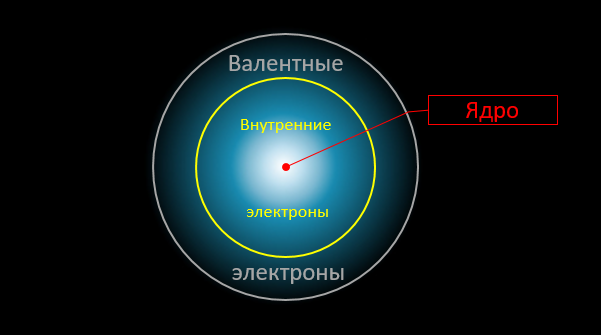
Now, attention, the question is: what is the maximum possible energy that can be released during such a "permutation"? Obviously, it cannot exceed the sum of the binding energies of external electrons with atoms (in the final and initial products). But these binding energies are well known to us ^{[ 285 ]} . The calculation for one atom they constitute 1.5 - 25 electron volts ( eV ) and are expressed in fractions of the Rydberg constant - the magnitude of the fundamental, the constructed of the basic constants of our universe:

Ry (in Gauss system) = m _e e ⁴ /2 ħ ² = 1 3 . 6 eV [ 300 ]

At the same time, both 25 and 13.6 eV are unattainable. For in typical reactions, not all of the binding energy is released, but only its difference between the two configurations, and therefore the practical energy release limit of chemistry is 3-4 eV per atom. In terms of a typical kilogram of fuel + oxidizer, this is equivalent to 20-30 MJ of energy released. This is the value that sets the theoretical maximum gas flow rate of a chemical jet engine with direct combustion u = √ (2 q ) = √ (2 * 2.5 * 10 ⁷ ) ≈ 7000 m / s. Unachievable, of course, because it does not take into account losses to the internal degrees of freedom of molecules, dissociation, radiation, non-directional thermal motion, etc.

It may seem that table heat of combustion ^{[ 240 ]}(say, 120 MJ / kg for hydrogen) the figure above is contradicted. But the fact is that these heats are usually indicated per kilogram of fuel , without taking into account the oxidant required for its combustion. The rocket carries both components with it, and if you recalculate the energy released per kilogram of the mixture (with balanced combustion), a completely different picture emerges ^{[ 240 ] [ 250 ] [ 260 ]} :

Fuel + Oxidizer	Reaction	Heat value per kg. fuel, MJ / kg	For 1 kg of fuel you need an oxidizing agent, kg.	The heat of combustion of the mixture, MJ / kg	The yield on the atom mixture, eV
Hydrogen + Oxygen	2H 2 + O 2 = 2H 2 O	120	eight	13.3	0.83
Kerosene + oxygen	2C12H26 + 37O2 = 24CO2 + 26H2O	43	3.5	9.6	1.02
Уголь + кислород	C + O2 = CO2	33	2.7	9.0	1.38
Литий + кислород	4Li + O2 = 2Li2O	43.5	1.2	20.2	2.10
Бор + кислород	2B + 1.5O2 = B2O3	57.2	2.2	17.8	2.58
Магний + кислород	2Mg + O2 = 2MgO	25.1	0.7	15.1	3.18
Бериллий + кислород	2Be + O2 = 2BeO	66.6	1.8	24.0	3.12
Литий + фтор	2Li + F2 = 2LiF	88.8	2.7	23.7	3.21
Бериллий + фтор	Be + F2 = BeF2	114	4.2	21.9	3.57
Дицианоацетилен + озон	C 4 N 2 + (4/3) O 3 = 4CO + N 2	16.2	0.8	8.8	1.28

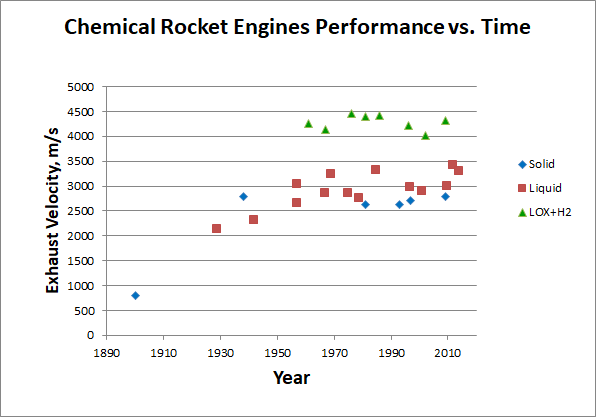
As we see, even the most energy-intensive, albeit unsuitable for practical use, fuels provide only 24 MJ / kg of heat during combustion. And we have rested against this limit almost from the beginning of cosmonautics, which shows a graph of the speed of the discharge of chemical engines depending on the year they were created:



[Early engines according to [ 310 ], [ 320 ], [ 330 ], later - Wikipedia individually. Data collection here ]

It seems that the potential of chemical fuels has long been developed. Do not start to store energy in another form?

Continued.