Precise rotation of the bitmap image at an arbitrary angle
Rotating a raster image by angles that are multiples of 90 ° relative to the geometric center of the image is a trivial task and can be solved without loss of quality by simply converting the coordinates of each pixel.
To rotate the bitmap image at an arbitrary angle, fast but not optimal algorithms have been developed that give an approximation acceptable for practical purposes with loss of quality (for example, this one ).
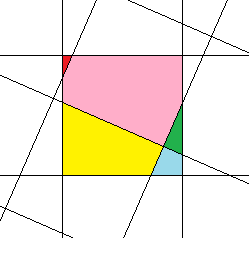 Quite a long time ago, out of purely sporting interest, I was interested in the task of the most accurate rotation of the bitmap image at an arbitrary angle. Unfortunately, I could not find a ready-made algorithm anywhere, so I had to do it myself. Even if in the end I “invented the bicycle”, the result, it seems to me, turned out to be interesting enough to be shared.
Quite a long time ago, out of purely sporting interest, I was interested in the task of the most accurate rotation of the bitmap image at an arbitrary angle. Unfortunately, I could not find a ready-made algorithm anywhere, so I had to do it myself. Even if in the end I “invented the bicycle”, the result, it seems to me, turned out to be interesting enough to be shared.
Below we consider the algorithm for precision rotation of a raster image by an arbitrary angle relative to an arbitrary center with minimal loss.
I thank Kharchenko Vladislav Vladimirovich for the assistance provided.
It can be seen from the above figure that after the rotation of the raster image, the color of each pixel of the final image is determined by the addition of the colors of several “fragments” of several pixels of the original image, in proportion to the areas of the corresponding “fragments”. Therefore, in general terms, the solution to our problem will be to find the area of all “fragments” for each pixel of the original image and to collect the color of each pixel of the final image from the colors of the corresponding “fragments” .
As a pixel model of the source image, we will use a square with side = 1, with the following notation for the angles:
 i1 is the rightmost corner;
i1 is the rightmost corner;
i2 is the lowest corner;
i3 is the leftmost corner;
i4 is the topmost corner.
The model of the final image will be a grid of parallel horizontal and vertical lines with a distance between the lines = 1. The
coordinates of the center of rotation of the raster image, in this representation, can be expressed as a pair of arbitrary real numbers. That is, the center of rotation in our problem may lie not at the geometric center of the pixel and not at the intersection point of the grid lines, but at an arbitrary point in the Cartesian coordinates.
Since when you rotate the raster image, the square of each pixel rotates by the same angle (relative to the center of this pixel), we will solve the problem for one pixel, and then apply the resulting solution for each pixel of the original image.
Rotation of a raster image can be divided into two parts:
1. The rotation of the square of each pixel of the original image relative to the center of this square by a given angle.
2. The offset of the center of the square of the pixel in accordance with the angle of rotation of the image relative to the center of rotation of the image so that the square occupies its final position on the grid of the final image.
In this case, the grid of the final image cuts the square of each pixel of the original image into “fragments” in the amount of 4, 5 or 6 pieces.
To systematize the variety of the resulting options, I had to compile a taxonomy of all kinds of intersections of the square of the pixel of the source image with the grid of the final image. There were only 23 essentially different options:

Legend here are:
- the numbers in the cells indicate the numbers of the angles of the square of the pixel that fell into this cell of the grid of the final image after the image is rotated;
- the green color indicates the cells in which the pixel sections got and are guaranteed to be left there by a "fragment";
- the yellow color indicates the cells into which, depending on the conditions, “fragments” of the pixel square, which are formed not by the corners of the square, but by the sides of the square , may fall (or may not fall).
For clarity, I will give one of the possible variations of option No. 3:
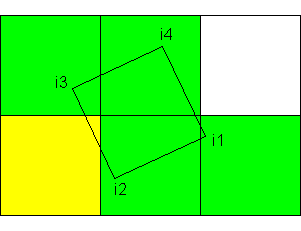
As you can see, the upper right cell does not contain a “fragment” of a pixel, although it could contain rotation under other conditions.
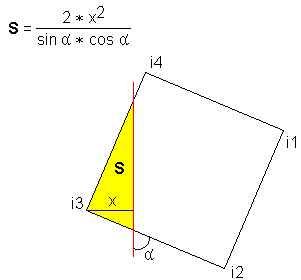
In order not to burden the reader with detailed geometrical calculations, I’ll say right away that in all these 23 variants the pixel of the original image is dissected into “fragments”, the area of which is easily calculated by combining 4 formulas. These formulas are illustrated below. Red color indicates the grid lines of the final image, which cut through the square of the pixel. The area, the area of which is calculated by the formula, is shaded in yellow.
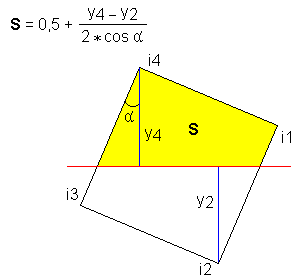 This formula is not used to calculate the final area of the "fragment", but it is convenient to use it for quick calculation of auxiliary intermediate areas, since we know that the area of the entire pixel = 1.
This formula is not used to calculate the final area of the "fragment", but it is convenient to use it for quick calculation of auxiliary intermediate areas, since we know that the area of the entire pixel = 1.
As input variables, all formulas use heights omitted from the corners of the square by the grid of the final image, for the simple reason that the calculation of these heights is reduced to the instantaneous selection of the fractional part of the numerical value of the coordinate of the corresponding corner of the square of the pixel.

This formula is used only in options 1 and 2.
 A frequently used formula is very good that it is quickly calculated. Since the rotation angle is the same for each pixel, all trigonometric functions can be counted once, before processing all the pixels, and then use these values in the loop as constants.
A frequently used formula is very good that it is quickly calculated. Since the rotation angle is the same for each pixel, all trigonometric functions can be counted once, before processing all the pixels, and then use these values in the loop as constants.
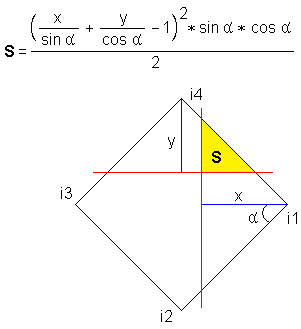 This formula is calculated in two steps. First, the expression in parentheses is evaluated. If it takes a positive value, then the area is calculated. If the value is negative, it means that the “splinter” formed by the angle of the grid and the side of the square does not cut off the pixel and there is no point in making further calculations.
This formula is calculated in two steps. First, the expression in parentheses is evaluated. If it takes a positive value, then the area is calculated. If the value is negative, it means that the “splinter” formed by the angle of the grid and the side of the square does not cut off the pixel and there is no point in making further calculations.
With all of the above, in general terms, the algorithm will look like this:
1. Load the original image into the computer memory.
2. We calculate the size of the final image in pixels.
3. We create an intermediate two-dimensional array, each element of which contains 3 RGB color components in the format of a floating-point number. The dimensions of the array are equal to the sizes of the final image.
4. Sequentially iterate over all the pixels of the original image; we turn each of them by a given angle and place it on the grid of the final image, calculating the 4 coordinates of the corners of the square of the pixel; we classify a pixel according to 23 options and consider the area of “fragments”; add the colors of the resulting “fragments” to the corresponding elements of the intermediate array in proportion to the area of these “fragments”.
5. After processing all the pixels of the original image, round the RGB values in the intermediate array to an integer value for each element and create the final image in BMP format based on these integer values.
Based on the above algorithm, a program for Windows was written. The source code for Object Pascal and the compiled executable can be downloaded here .
Program interface.
By clicking on the “Open ...” button, a dialog for selecting a BMP file opens. Bitmaps with only 24-bit palette are supported. An open image is displayed in a window. The full title of the file and image size are displayed in the window title.
In the field "Angle" sets the angle of rotation in degrees - any positive number.
When entering fractional numbers, both a period and a comma can be used as a decimal separator.
Radio buttons “CW” and “CCW” specify the direction of rotation: “clockwise” and “counterclockwise”, respectively.
In the “Background color” block, you can set the background color with which the boundary pixels of the image will be mixed. The default background color is black.
In the fields “Center X” and “Center Y” the coordinates of the center of rotation are set. It should be borne in mind that the origin is in the upper left corner of the image and Y increases downward. By default, the center of rotation is set in the geometric center of the loaded image.
By pressing the “Rotate” button or by pressing the Enter key, the image is rotated by a predetermined angle relative to a given rotation center and displayed in the window. Rotating the image by angles that are multiple of 90 ° is implemented according to a simplified scheme by simply converting the coordinates of the pixels of the original image, while the values of “Center X” and “Center Y” are ignored.
The running time of the algorithm in seconds is displayed under the "Rotate" button.
Using the “Save ...” button, the rotated image can be saved to a BMP file.
If the final image does not fit in the window - it is adjusted to the borders of the window with the StretchBlt API function - therefore, it is possible to evaluate the real quality of large images only from the saved BMP file.
To rotate the image to another angle, it does not need to be reloaded - the image from the selected file is rotated, and is not currently displayed in the window.
An image with dimensions of 1024 x 768 on a machine with a four-core 2.67 GHz processor is rotated by this program at an arbitrary angle, on average, in about 0.5 seconds. An image with dimensions of 4000 x 4000 - in about 10 seconds. The running time of the algorithm for different angles may differ due to the fact that the image at different angles is split into a different number of “fragments”, for the calculation of the areas which are spent, respectively, different time.
The intermediate array containing the color information of the pixels of the final image in the format of a floating point number is implemented as extended (10 bytes), so processing large images (approximately more than 5000 x 5000 pixels) can cause a memory overflow error. It is possible to improve the situation by applying a less accurate data type and storing the integer part of the number immediately in the final bitmap, leaving only the fractional part in the auxiliary array.
Let us conduct a comparative analysis of the operation of the precision algorithm and the image rotation algorithm implemented in Photoshop.
For the first test, I took a very simple image - a horizontal black line 1 pixel thick and 10 pixels long, offset from the center of the white square with dimensions 100 x 100 pixels:

After which I turned this image relative to the point with coordinates (0, 0) by 3 ° clockwise. The point (0, 0) was chosen because, judging by my experiments, Photoshop rotates the image relative to this particular point. Here is the comparative result (increased 24 times):
Precision algorithm
Photoshop 7.0.1
Photoshop CS6 (64 Bit)
The Photoshop algorithm gives a more contrasting picture, the precision algorithm somewhat “blurs” the image. But in general, with a visual assessment, the result is almost the same. Along the way, we note that the rotation algorithm implemented in Photoshop has not undergone significant changes in 10 years.
For the second test, I chose a tulip from the standard Win7 distribution:

After rotating this image 5 ° clockwise relative to the geometric center, I summed up the color of all the pixels in the context of the RGB channels. Here is the result for the precision algorithm and the Photoshop algorithm:
The numbers in parentheses indicate the absolute deviation of this indicator from the original.
The color of the image after a precision rotation and before rounding has not practically changed - which is to be expected.
The biggest deviation, in this particular case, we find on channel G for the Photoshop algorithm. In percentage terms, this deviation is only 0.06%, therefore, “by eye” it is not noticeable, but for reasons of perfectionism, the result in Photoshop is worse than in the precision algorithm.
It is important to note that rounding the color of each pixel in the precision algorithm to the integer value necessary for the BMP format irreversibly destroys some of the color information.
For a visual comparison of the two algorithms, I’ll give an enlarged fragment of the image,

rotated 5 ° clockwise, respectively, Photoshop:

and precision algorithm:

A comparative analysis shows that Photoshop better preserves the contrasting elements of the image, but at the same time creates a "ghosting" of distorted color. The precision algorithm does not distort the color, but at the same time somewhat “blurs” the image.
1. Precise and at the same time relatively quick rotation of the bitmap image at an arbitrary angle is possible. For me, the question remains why professional graphic editors do not have an option that allows the user to rotate the image very accurately in a little more time.
2. Despite the extreme accuracy of the considered algorithm, the inverse image transformation, ie rotation to the opposite angle without loss of quality is impossible, because rounding the exact color value (in the format of a floating-point number) irreversibly destroys part of the color information.
3. From the point of view of visual perception of contrasting details, the best result is provided by the Photoshop optimal algorithm. Precision algorithm makes sense to apply in cases where it is important to maintain maximum information about the color of the image.
UPD:For practical use, I wrote a program that implements a simplified algorithm in which for each pixel of the final image all the necessary pieces of pixels of the original image are calculated sequentially and the color is rounded off immediately. Only after that the next pixel of the final image is calculated. In this case, the program accesses a single pixel of the source image several times. Thus, the calculation time has increased, on average, 1.7 times, but the memory in this version of the algorithm is spent only on storing bitmaps, which allows you to work with large images. Download the program and sources here .
To rotate the bitmap image at an arbitrary angle, fast but not optimal algorithms have been developed that give an approximation acceptable for practical purposes with loss of quality (for example, this one ).
 Quite a long time ago, out of purely sporting interest, I was interested in the task of the most accurate rotation of the bitmap image at an arbitrary angle. Unfortunately, I could not find a ready-made algorithm anywhere, so I had to do it myself. Even if in the end I “invented the bicycle”, the result, it seems to me, turned out to be interesting enough to be shared.
Quite a long time ago, out of purely sporting interest, I was interested in the task of the most accurate rotation of the bitmap image at an arbitrary angle. Unfortunately, I could not find a ready-made algorithm anywhere, so I had to do it myself. Even if in the end I “invented the bicycle”, the result, it seems to me, turned out to be interesting enough to be shared.Below we consider the algorithm for precision rotation of a raster image by an arbitrary angle relative to an arbitrary center with minimal loss.
I thank Kharchenko Vladislav Vladimirovich for the assistance provided.
Algorithm
It can be seen from the above figure that after the rotation of the raster image, the color of each pixel of the final image is determined by the addition of the colors of several “fragments” of several pixels of the original image, in proportion to the areas of the corresponding “fragments”. Therefore, in general terms, the solution to our problem will be to find the area of all “fragments” for each pixel of the original image and to collect the color of each pixel of the final image from the colors of the corresponding “fragments” .
As a pixel model of the source image, we will use a square with side = 1, with the following notation for the angles:
 i1 is the rightmost corner;
i1 is the rightmost corner; i2 is the lowest corner;
i3 is the leftmost corner;
i4 is the topmost corner.
The model of the final image will be a grid of parallel horizontal and vertical lines with a distance between the lines = 1. The
coordinates of the center of rotation of the raster image, in this representation, can be expressed as a pair of arbitrary real numbers. That is, the center of rotation in our problem may lie not at the geometric center of the pixel and not at the intersection point of the grid lines, but at an arbitrary point in the Cartesian coordinates.
Since when you rotate the raster image, the square of each pixel rotates by the same angle (relative to the center of this pixel), we will solve the problem for one pixel, and then apply the resulting solution for each pixel of the original image.
Rotation of a raster image can be divided into two parts:
1. The rotation of the square of each pixel of the original image relative to the center of this square by a given angle.
2. The offset of the center of the square of the pixel in accordance with the angle of rotation of the image relative to the center of rotation of the image so that the square occupies its final position on the grid of the final image.
In this case, the grid of the final image cuts the square of each pixel of the original image into “fragments” in the amount of 4, 5 or 6 pieces.
To systematize the variety of the resulting options, I had to compile a taxonomy of all kinds of intersections of the square of the pixel of the source image with the grid of the final image. There were only 23 essentially different options:

Legend here are:
- the numbers in the cells indicate the numbers of the angles of the square of the pixel that fell into this cell of the grid of the final image after the image is rotated;
- the green color indicates the cells in which the pixel sections got and are guaranteed to be left there by a "fragment";
- the yellow color indicates the cells into which, depending on the conditions, “fragments” of the pixel square, which are formed not by the corners of the square, but by the sides of the square , may fall (or may not fall).
For clarity, I will give one of the possible variations of option No. 3:

As you can see, the upper right cell does not contain a “fragment” of a pixel, although it could contain rotation under other conditions.
In order not to burden the reader with detailed geometrical calculations, I’ll say right away that in all these 23 variants the pixel of the original image is dissected into “fragments”, the area of which is easily calculated by combining 4 formulas. These formulas are illustrated below. Red color indicates the grid lines of the final image, which cut through the square of the pixel. The area, the area of which is calculated by the formula, is shaded in yellow.
Formula 1
 This formula is not used to calculate the final area of the "fragment", but it is convenient to use it for quick calculation of auxiliary intermediate areas, since we know that the area of the entire pixel = 1.
This formula is not used to calculate the final area of the "fragment", but it is convenient to use it for quick calculation of auxiliary intermediate areas, since we know that the area of the entire pixel = 1. As input variables, all formulas use heights omitted from the corners of the square by the grid of the final image, for the simple reason that the calculation of these heights is reduced to the instantaneous selection of the fractional part of the numerical value of the coordinate of the corresponding corner of the square of the pixel.
Formula 2

This formula is used only in options 1 and 2.
Formula 3
 A frequently used formula is very good that it is quickly calculated. Since the rotation angle is the same for each pixel, all trigonometric functions can be counted once, before processing all the pixels, and then use these values in the loop as constants.
A frequently used formula is very good that it is quickly calculated. Since the rotation angle is the same for each pixel, all trigonometric functions can be counted once, before processing all the pixels, and then use these values in the loop as constants.Formula 4
 This formula is calculated in two steps. First, the expression in parentheses is evaluated. If it takes a positive value, then the area is calculated. If the value is negative, it means that the “splinter” formed by the angle of the grid and the side of the square does not cut off the pixel and there is no point in making further calculations.
This formula is calculated in two steps. First, the expression in parentheses is evaluated. If it takes a positive value, then the area is calculated. If the value is negative, it means that the “splinter” formed by the angle of the grid and the side of the square does not cut off the pixel and there is no point in making further calculations. With all of the above, in general terms, the algorithm will look like this:
1. Load the original image into the computer memory.
2. We calculate the size of the final image in pixels.
3. We create an intermediate two-dimensional array, each element of which contains 3 RGB color components in the format of a floating-point number. The dimensions of the array are equal to the sizes of the final image.
4. Sequentially iterate over all the pixels of the original image; we turn each of them by a given angle and place it on the grid of the final image, calculating the 4 coordinates of the corners of the square of the pixel; we classify a pixel according to 23 options and consider the area of “fragments”; add the colors of the resulting “fragments” to the corresponding elements of the intermediate array in proportion to the area of these “fragments”.
5. After processing all the pixels of the original image, round the RGB values in the intermediate array to an integer value for each element and create the final image in BMP format based on these integer values.
Program
Based on the above algorithm, a program for Windows was written. The source code for Object Pascal and the compiled executable can be downloaded here .
Program interface.
By clicking on the “Open ...” button, a dialog for selecting a BMP file opens. Bitmaps with only 24-bit palette are supported. An open image is displayed in a window. The full title of the file and image size are displayed in the window title.
In the field "Angle" sets the angle of rotation in degrees - any positive number.
When entering fractional numbers, both a period and a comma can be used as a decimal separator.
Radio buttons “CW” and “CCW” specify the direction of rotation: “clockwise” and “counterclockwise”, respectively.
In the “Background color” block, you can set the background color with which the boundary pixels of the image will be mixed. The default background color is black.
In the fields “Center X” and “Center Y” the coordinates of the center of rotation are set. It should be borne in mind that the origin is in the upper left corner of the image and Y increases downward. By default, the center of rotation is set in the geometric center of the loaded image.
By pressing the “Rotate” button or by pressing the Enter key, the image is rotated by a predetermined angle relative to a given rotation center and displayed in the window. Rotating the image by angles that are multiple of 90 ° is implemented according to a simplified scheme by simply converting the coordinates of the pixels of the original image, while the values of “Center X” and “Center Y” are ignored.
The running time of the algorithm in seconds is displayed under the "Rotate" button.
Using the “Save ...” button, the rotated image can be saved to a BMP file.
If the final image does not fit in the window - it is adjusted to the borders of the window with the StretchBlt API function - therefore, it is possible to evaluate the real quality of large images only from the saved BMP file.
To rotate the image to another angle, it does not need to be reloaded - the image from the selected file is rotated, and is not currently displayed in the window.
An image with dimensions of 1024 x 768 on a machine with a four-core 2.67 GHz processor is rotated by this program at an arbitrary angle, on average, in about 0.5 seconds. An image with dimensions of 4000 x 4000 - in about 10 seconds. The running time of the algorithm for different angles may differ due to the fact that the image at different angles is split into a different number of “fragments”, for the calculation of the areas which are spent, respectively, different time.
The intermediate array containing the color information of the pixels of the final image in the format of a floating point number is implemented as extended (10 bytes), so processing large images (approximately more than 5000 x 5000 pixels) can cause a memory overflow error. It is possible to improve the situation by applying a less accurate data type and storing the integer part of the number immediately in the final bitmap, leaving only the fractional part in the auxiliary array.
results
Let us conduct a comparative analysis of the operation of the precision algorithm and the image rotation algorithm implemented in Photoshop.
Test 1
For the first test, I took a very simple image - a horizontal black line 1 pixel thick and 10 pixels long, offset from the center of the white square with dimensions 100 x 100 pixels:

After which I turned this image relative to the point with coordinates (0, 0) by 3 ° clockwise. The point (0, 0) was chosen because, judging by my experiments, Photoshop rotates the image relative to this particular point. Here is the comparative result (increased 24 times):
Precision algorithm
Photoshop 7.0.1
Photoshop CS6 (64 Bit)
The Photoshop algorithm gives a more contrasting picture, the precision algorithm somewhat “blurs” the image. But in general, with a visual assessment, the result is almost the same. Along the way, we note that the rotation algorithm implemented in Photoshop has not undergone significant changes in 10 years.
Test 2
For the second test, I chose a tulip from the standard Win7 distribution:
After rotating this image 5 ° clockwise relative to the geometric center, I summed up the color of all the pixels in the context of the RGB channels. Here is the result for the precision algorithm and the Photoshop algorithm:
Original | Precision rotation | Precision Turn | Photoshop CS6 |
| R = 33381406 G = 27933900 B = 11239213 | R = 33381406.0000004 (~ 0) G = 27933899.9999997 (~ 0) B = 11239212.9999999 (~ 0) | R = 33382786 (1380) G = 27933920 (20) B = 11238086 (-1127) | R = 33387726 (6320) G = 27950823 (16923) B = 11245937 (6724) |
The color of the image after a precision rotation and before rounding has not practically changed - which is to be expected.
The biggest deviation, in this particular case, we find on channel G for the Photoshop algorithm. In percentage terms, this deviation is only 0.06%, therefore, “by eye” it is not noticeable, but for reasons of perfectionism, the result in Photoshop is worse than in the precision algorithm.
It is important to note that rounding the color of each pixel in the precision algorithm to the integer value necessary for the BMP format irreversibly destroys some of the color information.
For a visual comparison of the two algorithms, I’ll give an enlarged fragment of the image,
rotated 5 ° clockwise, respectively, Photoshop:

and precision algorithm:

A comparative analysis shows that Photoshop better preserves the contrasting elements of the image, but at the same time creates a "ghosting" of distorted color. The precision algorithm does not distort the color, but at the same time somewhat “blurs” the image.
conclusions
1. Precise and at the same time relatively quick rotation of the bitmap image at an arbitrary angle is possible. For me, the question remains why professional graphic editors do not have an option that allows the user to rotate the image very accurately in a little more time.
2. Despite the extreme accuracy of the considered algorithm, the inverse image transformation, ie rotation to the opposite angle without loss of quality is impossible, because rounding the exact color value (in the format of a floating-point number) irreversibly destroys part of the color information.
3. From the point of view of visual perception of contrasting details, the best result is provided by the Photoshop optimal algorithm. Precision algorithm makes sense to apply in cases where it is important to maintain maximum information about the color of the image.
UPD:For practical use, I wrote a program that implements a simplified algorithm in which for each pixel of the final image all the necessary pieces of pixels of the original image are calculated sequentially and the color is rounded off immediately. Only after that the next pixel of the final image is calculated. In this case, the program accesses a single pixel of the source image several times. Thus, the calculation time has increased, on average, 1.7 times, but the memory in this version of the algorithm is spent only on storing bitmaps, which allows you to work with large images. Download the program and sources here .
