Programming in Maxima

Lesson Maxima

Introduction

Maxima is a free computer algebra system (CAS) based on Common Lisp. In its functionality, it is hardly inferior to other modern paid CAS, such as Mathcad, Mathematica, Maple; can carry out analytical (symbolic) calculations, numerical calculations, build graphs (using gnuplot). It is possible to write scripts and even translate them into Common Lisp code, followed by compilation. In view of the fact that maxima was written from developed by lisp programmers, its syntax may seem somewhat confusing, since the language is immediately both imperative and functional. I will try to clarify precisely these points and explain the essence of the functional approach in an accessible way, and I will not focus at all on specific mathematical functions: they are quite easy to master independently.

Shell

Of course, calling the maxima interpreter from the console is not very convenient. We want to look at beautiful formulas that are rendered with latex. Therefore, for beginners, I would advise you to put the wxMaxima shell . If you are fond of TeXmacs - you can configure it as a shell (to be honest, I have not tried it). Well, for lovers of emacs there is imaxima , to work in the buffer. It is literally put out of the box.

Acquaintance

At first glance, everything is simple: we introduce an expression ending with a semicolon, we get the answer. You can try maxima as a calculator, calculate the sum of two numbers, calculate the sine of the angle, etc. We dig deeper what is happening.

Atoms

Symbols, numbers, and logical constants true and false are the simplest objects in the system. All other expressions and structures of the language are built from them, therefore they are called atomic (indivisible) or simply atoms.

Variables

The system distinguishes between free and signaled variables. The indicated variables are related variables, the variables to which some value is assigned. When interpreting, the variable name is replaced with its value. You can set a variable using the ":" sign. Free variables are not associated with any value and we can operate with them abstractly, for example, add two symbolic expressions.

Computation Context

When calculating each command, its computational context is formed. It is a collection of relationships between variable names and their values, as well as some interpretation parameters. There are two computational contexts: local and global. The global context - common to all interpreted commands, determines the current state of the interpreter. A local context is created for the duration of the execution of one command, and is valid only for it. The highest priority is the connection and local context settings.

Here the value of the variable a is taken from the global context, and for the local one the option to deploy works is established, i.e. further works will not be deployed on their own.

Compute Lock

Let's try to add two variables. And now put in front of them a single quote symbol. This is a blocking calculation operator. If we put it before the variable name - as a result we get the name of this variable, before the function call - the symbolic expression of the function call. What for? Sometimes you may need to use one function to process the expression of another function and get a function or number as the output, for example, calculating an indefinite integral. In other words, you have the ability to represent the expression as data and manipulate it. However, if you try to stop the calculation of the sum of two numbers, then the calculations will not stop. This is due to the fact that the single quote operator does not stop the simplest simplification of the expression (simple operations on numbers, reduction of fractions). Also, the calculations will not stop,
And so, the Maxima system does not distinguish between algorithmic functions and mathematical functions, in it they are one language element. In the terminology of the interpreter itself, the operators that can be calculated are called verb, those operators that remain so uncomputed are called noun. To initiate the calculation of all noun, it is necessary to set the nouns option in the context of calculations.

Calculations

We learned that the interpreter distinguishes between the concepts of a symbolic expression and its calculation. In what cases does the calculation take place? The most obvious case is when we try to calculate some kind of expression (2 + 3, for example). They entered the expression - got its meaning. They calculated the function of the argument - got the value. Enter the variable name - get its value. We learned that the value of a variable can be either an atom or a symbolic expression. When else is the calculation? The calculation occurs when a variable is assigned a value. The value to the right of the colon is calculated before the assignment, so when assigning a variable to a symbolic expression, we put a quotation mark to stop this calculation. There is a special kind of assignment (two colon operator) when evaluating both the expression on the right and the expression on the left.

The result of calculating the variable a on the left is the variable b.

Example

Consider a simple example - building the set of all subsets. As it turned out, Maxima has built-in types for working with sets, but, alas, there is no such function. Write it.

To begin with, let’s see what sets are. The sets in Maxima appear to be based on a different data structure — singly linked lists. What is a list everyone understands. They have three main functions for working with them: getting an element in the head of the list (first), getting a list consisting of the original without the first element (rest), adding a new element to the beginning (cons) and combining two lists (append). Similar functions exist in any lisp implementation, but most often they are called slightly differently: car, cdr, cons, append, respectively.

How do you usually imagine an algorithm for solving such a problem? It would be possible to represent subsets in the form of a characteristic vector and iterate over all of them. However, we will show precisely the functional approach. It is easy to see that each element is included in exactly half of the subsets. This simple fact is already enough to build a recursive algorithm. We remove one element a from the set A. The set of all subsets of A will consist of the union of the set of all subsets A \ a and the set of all subsets A \ a, where a is added to each element. Using the last statement, you can recursively lower the dimension of the problem arbitrarily, reducing it to the trivial case. For implementation, we need an additional function of two parameters (element and set of sets), which would add the specified element to each set.

Note that function declarations occur almost like in mathematics. It should be noted that in determining the right-hand side after the sign is not calculated. (In order to define a function so that its definition is computed, use the define form). A new computational form appears here. It works the same way as in imperative languages. When the condition is met, the expression is evaluated after then, if not, after else. Now we write the desired function.

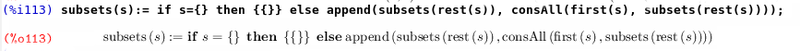
Let's try something to count.

the end

That's it. In the next article, it would be nice to describe the implementation of the steepest gradient descent.