Richard Hamming: Chapter 10. Coding Theory - I

“The goal of this course is to prepare you for your technical future.”

Hi, Habr. Remember the awesome article "You and your work" (+219, 2442 bookmarks, 394k readings)?

So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book written based on his lectures. We translate it, because the man says it.

This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes the conditions that increase the chances of doing a great job. ”

We have already translated 28 (out of 30) chapters. And we are working on the publication "in paper."

Coding Theory - I

Having considered computers and the principle of their work, we will now consider the issue of information representation: how computers represent the information we want to process. The value of any character may depend on the way it is processed, the machine has no specific meaning for the bit used. When discussing the history of software in Chapter 4, we considered some synthetic programming language, in it the instruction code of the breakpoint coincided with the code of other instructions. This situation is typical for most languages, the meaning of the instruction is determined by the corresponding program.

To simplify the problem of presenting information, consider the problem of transferring information from point to point. This question is related to the issue of conservation information. The problems of information transmission in time and space are identical. Figure 10.1 shows the standard information transfer model.



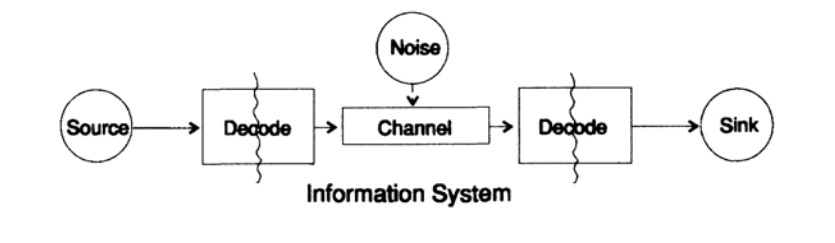
Figure 10.1

On the left in Figure 10.1 is the source of the information. When considering the model, the nature of the source is not important to us. It can be a set of alphabet characters, numbers, mathematical formulas, musical notes, symbols with which we can represent dance movements - the nature of the source and the meaning of the symbols stored in it are not part of the transmission model. We consider only the source of information, with such a restriction a powerful, general theory is obtained that can be extended to many areas. It is an abstraction from many applications.

When at the end of the 1940s Shannon created the theory of information, it was thought that it should have been called communication theory, but he insisted on the term information. This term has become a permanent cause of both increased interest and constant disillusionment with theory. Investigators wanted to build whole “information theories”, they degenerated into the set of characters theory. Returning to the transmission model, we have a source of data that needs to be encoded for transmission.

The coder consists of two parts, the first part is called the source coder, the exact name depends on the type of source. Different data types correspond to different types of encoders.

The second part of the encoding process is called channel coding and depends on the type of channel for data transmission. Thus, the second part of the encoding process is consistent with the type of transmission channel. Thus, when using standard interfaces, data from the source at the beginning is encoded according to the requirements of the interface, and then according to the requirements of the used data channel.

According to the model, in Figure 10.1, the data channel is exposed to “additional random noise”. All noise in the system is combined at this point. It is assumed that the encoder receives all symbols without distortion, and the decoder performs its function without errors. This is some idealization, but for many practical purposes it is close to reality.

The decoding phase also consists of two stages: a channel — a standard, a standard — a data receiver. At the end of the data transfer is transmitted to the consumer. And again we do not consider the question of how the consumer interprets this data.

As noted earlier, the data transmission system, for example, telephone messages, radio, TV programs, represents the data as a set of numbers in the computer's registers. Again, the transmission in space is not different from the transmission in time or the preservation of information. Do you have information that will take some time, then it needs to be encoded and stored on the data storage source. If necessary, the information is decoded. If the encoding and decoding system is the same, we transmit the data through the transmission channel without changes.

The fundamental difference between the presented theory and the conventional theory in physics is the assumption that there is no noise in the source and the receiver. In fact, errors occur in any equipment. In quantum mechanics, noise occurs at any stage according to the principle of uncertainty, and not as the initial condition; in any case, the concept of noise in information theory is not equivalent to a similar concept in quantum mechanics.
For definiteness, we will further consider the binary form of data representation in the system. Other forms are processed in a similar way, for simplicity, we will not consider them.

We begin our consideration of systems with coded characters of variable length, as in the classic Morse code of dots and dashes, in which frequently encountered characters are short and rare are long characters. This approach allows to achieve high efficiency code, but it is worth noting that Morse code is ternary, not binary, since it contains a space character between dots and a dash. If all the characters in the code are of the same length, then this code is called block.

The first obvious necessary property of the code is the ability to unambiguously decode a message in the absence of noise, at least this seems to be a desirable property, although in some situations this requirement can be neglected. Data from the transmission channel for the receiver looks like a stream of characters from zeros and ones.

We will call two adjacent characters a double extension, three adjacent characters a triple extension, and in the general case if we send N characters, the receiver sees additions to the base code of N characters. The receiver, without knowing the value of N, must divide the stream into broadcast blocks. Or, in other words, the receiver must be able to decompose the stream in a unique way in order to restore the original message.

Consider a alphabet of a small number of characters, usually alphabets are much larger. The alphabets of languages ​​start from 16 to 36 characters, including upper and lower case characters, numbers, and punctuation. For example, in an ASCII table 128 = 2 ^ 7 characters.
Consider a special code consisting of 4 characters s1, s2, s3, s4

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

How should the receiver interpret the following

0011 expression received ?

Like s1s1s4 or like s2s4 ?

You can not uniquely answer this question, this code is definitely not decoded, therefore, it is unsatisfactory. On the other hand, the code

s1 = 0; s2 = 10; s3 = 110; s4 = 111

decodes the message in a unique way. Take an arbitrary string and consider how the receiver will decode it. You need to build a decoding tree. According to the form in Figure 10.II. Line

1101000010011011100010100110 ...

can be broken into blocks of characters

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110, ...

according to the following decoding tree construction rule:

If you are at the top of the tree, then read the next character. When you reach a leaf of a tree, you convert the sequence into a symbol and go back to the start.

The reason for the existence of such a tree is that no symbol is a prefix of another, so you always know when it is necessary to return to the beginning of the decoding tree.

It is necessary to pay attention to the following. First, decoding is a strictly flow process, in which each bit is examined only once. Secondly, the protocols usually include characters that are a marker for the end of the decoding process and are necessary to mark the end of the message.

Failure to use the terminating symbol is a common mistake when designing codes. Of course, you can provide a constant decoding mode, in this case the final character is not needed.



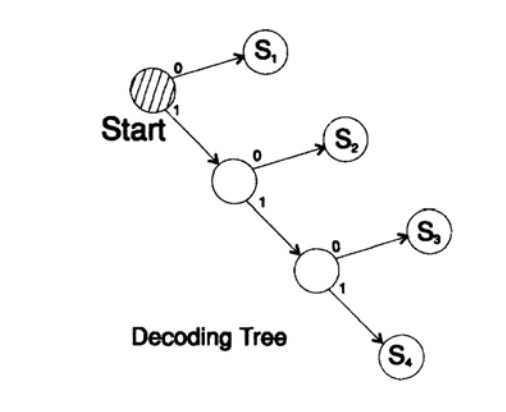
Figure 10.II

The next question is the codes for stream (instant) decoding. Consider the code that is obtained from the previous one by the display of symbols

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Suppose we get the sequence 011111 ... 111 . The only way to decode the message text is to group the bits from the end by 3 in the group and select the groups with leading zero before the ones, after which you can decode. Such code is decoded in the only way, but not instant! To decode, you must wait for the transfer to complete! In practice, this approach levels the decoding speed (Macmillan's theorem), therefore, it is necessary to look for ways of instant decoding.

Consider two ways to encode the same character, Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

Tree decoding of this method is presented in Figure 10.III.



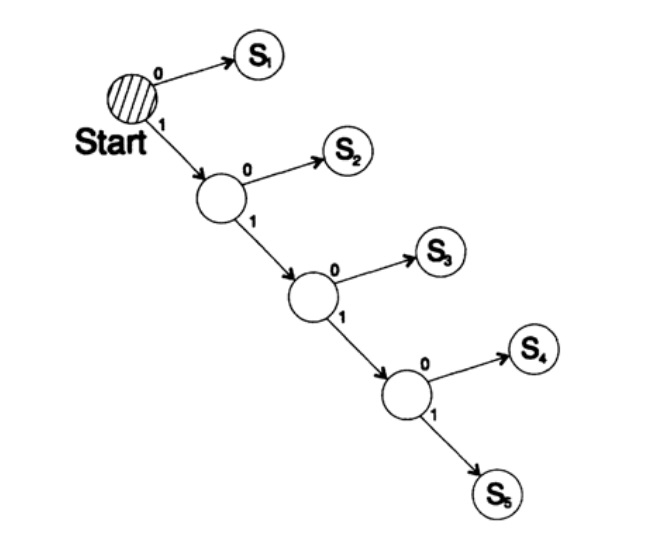
Figure 10.III The

second method

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111 ,

The decoding tree of this care is presented in figure 10.IV.

The most obvious way to measure code quality is the average length for a certain set of messages. To do this, it is necessary to calculate the code length of each character multiplied by the corresponding probability of occurrence of pi. Thus, the length of the entire code is obtained. The formula for the average length L of the code for an alphabet of q characters is as follows.



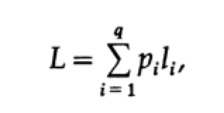
where pi is the probability of occurrence of the symbol si, li is the corresponding length of the encoded symbol. For effective code, the value of L should be as small as possible. If P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 and p5 = 1/16, then for code # 1 we get the length of code



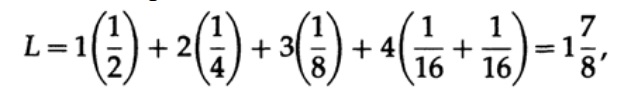
A for code # 2



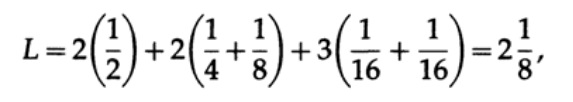
The obtained values ​​indicate preference first code.
If all the words in the alphabet have the same probability of occurrence, then the second code is more preferable. For example, when pi = 1/5 the length of code # 1



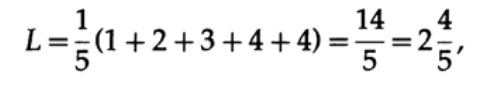
and the length of code # 2,



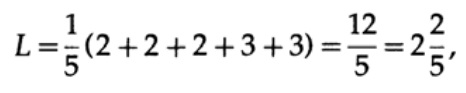
this result shows the preference of 2 codes. Thus, when developing a “good” code, it is necessary to take into account the probability of symbols.



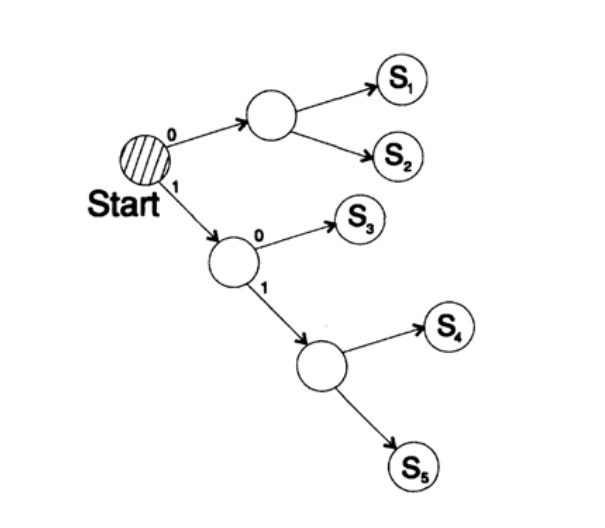
Figure 10.IV



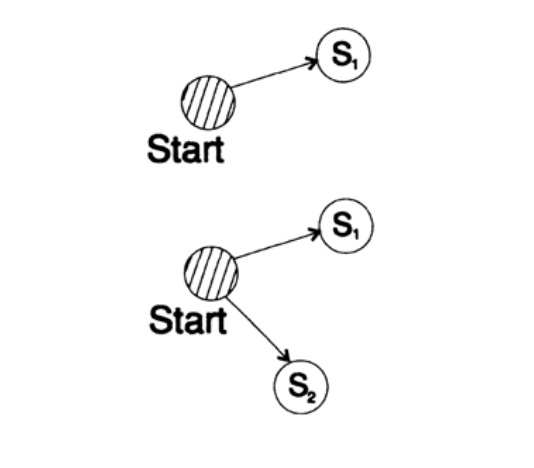
Figure 10.V

Consider the Kraft inequality, which determines the limit value of the length of the code of the symbol li. According to the basis of 2, the inequality is represented as



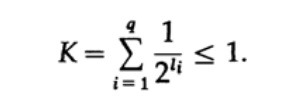
This inequality says that there can not be too many short characters in the alphabet, otherwise the sum will be quite large.

To prove the Kraft inequality for any fast unique decoded code, we construct a decoding tree and apply the mathematical induction method. If a tree has one or two leaves, as shown in Figure 10.V, then without a doubt the inequality is true. Further, if the tree has more than two leaves, then we divide the tree long m into two subtrees. According to the principle of induction, we assume that the inequality is true for each branch of height m -1 or less. According to the principle of induction, applying the inequality to each branch. Denote the length of the codes of the branches K 'and K' '. When two branches of a tree are combined, the length of each increases by 1, therefore, the code length consists of the sums K '/ 2 and K' '/ 2, the



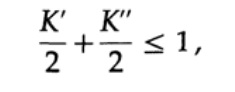
theorem is proved.

Consider the proof of the Macmillan theorem. Apply the Kraft inequality to decode codes that are not thread safe. The proof is based on the fact that for any number K> 1 the nth power of the number is certainly greater than a linear function of n, where n is a rather large number. Let us raise the Kraft inequality to the nth degree and represent the expression as the sum



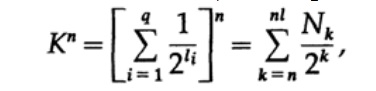
where Nk is the number of characters of length k, summation starts with the minimum length of the nth character representation and ends with the maximum length nl, where l is the maximum length of the encoded character. From the requirement of a unique decoding, it follows that. The sum is represented as



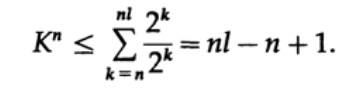
If K> 1, then it is necessary to set n rather large in order for the inequality to become false. Therefore, k <= 1; Macmillan's theorem is proved.

Consider a few examples of the application of Kraft inequality. Can there be a uniquely decoded code with lengths of 1, 3, 3, 3? Yes, since



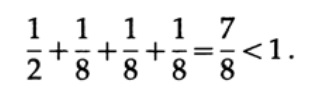
what about lengths 1, 2, 2, 3? Calculate according to the formula



Inequality is violated! There are too many short characters in this code.

Point codes (comma codes) are codes that consist of characters 1, terminated by the symbol 0, except for the last character consisting of all ones. One of the special cases is the code

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5 = 11111.

For this code, we get an expression for the Kraft inequality



In this case, we achieve equality. It is easy to see that for point codes, Kraft's inequality degenerates into equality.

When building a code, you need to pay attention to the amount of Kraft. If the sum of Kraft begins to exceed 1, then this is a signal about the need to include a symbol of another length to reduce the average code length.

It should be noted that the Kraff's inequality does not mean that this code is uniquely decodable, but that there is a code with symbols of such length that are uniquely decoded. To build a unique decoded code, you can assign the corresponding bit length li to a binary number. For example, for lengths of 2, 2, 3, 3, 4, 4, 4, 4 we obtain the Kraft inequality.



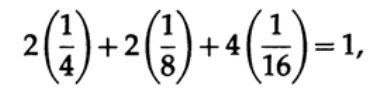
Therefore, there can be such a unique decodable streaming code.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

I want to draw attention to what is really happening when we exchange ideas. For example, at this moment in time I want to transfer the idea from my head to yours. I pronounce some words by means of which, I believe, you will be able to understand (get) this idea.

But when a little later you want to convey this idea to your friend, you will almost certainly say completely different words. In fact, the meaning or meaning is not enclosed within some specific words. I used some words, and you can use completely different words to convey the same idea. Thus, different words can convey the same information. But, as soon as you tell your interlocutor that you do not understand the message, then as a rule, the interlocutor will pick up a different set of words, the second or even the third, to convey meaning. Thus, the information is not enclosed in a set of certain words. As soon as you have received certain words, do a great job when translating words into an idea that the other person wants to convey to you.

We are learning to pick words in order to fit under the interlocutor. In a sense, we choose words according to our thoughts and the noise level in the channel, although such a comparison does not accurately reflect the model that I use to represent the noise in the decoding process. In large organizations, the inability of the interlocutor to hear what another person has said is a serious problem. In high positions, employees hear what they want to hear. In some cases, you need to remember this when you move up the career ladder. The presentation of information in a formal form is a partial reflection of the processes from our life and has found wide application far beyond the limits of formal rules in computer applications.

To be continued...

Who wants to help with the translation, layout and publication of the book - write in a personal or mail magisterludi2016@yandex.ru

By the way, we also launched another translation of the coolest book - “The Dream Machine: The History of Computer Revolution” )