Amplitude modulation on fingers
In a recent article “ Amplitude Modulation of an Arbitrary Signal, ” its author rather messyly tried to present his understanding of spectrum shaping with amplitude modulation. But the lack of illustrations and the abundance of mathematics with the involvement of integral transformations prevented the community from understanding the author’s thoughts and appreciating the article; while the topic is quite simple - and we will try to consider it again, this time with pictures and Wolfram Mathematica attraction.
So, the idea of amplitude modulation is to transmit a low-frequency signal — voice or music — by modulating a high-frequency (carrier) signal that is many times larger than the audible range and occupies a narrow frequency band on the radio. The modulation itself is performed by simply multiplying the signal by the carrier:

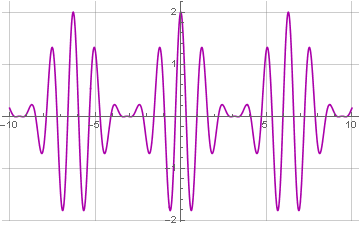
Here we have as a carrier a sinusoid with a frequency of 5:


And the signal itself - with a frequency of 1:


You can see that the signal is shifted up and has only positive values. This is not accidental and is a prerequisite for the possibility of its subsequent correct recovery. How to restore it? Very simple! It is necessary to shift the phase of the modulated signal by 90 degrees (an operation known as the Hilbert transform ) and calculate the root of the sum of squares of the modulated and transformed signals:

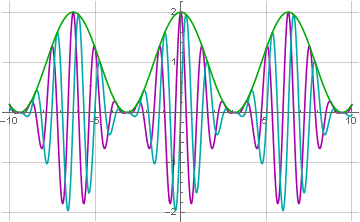
In a simpler (but coarse) version, the Hilbert transform can be replaced by a one-quarter delay in the carrier frequency, and the resulting signal can be additionally filtered out with a low-pass filter. In an even simpler version, it is possible not to count the roots and squares at all, but to filter the signal by absolute value (which is usually used in radio receivers).
Now let's see what happens with the spectra. We calculate the Fourier transform of the carrier:


Since the Dirac's delta function is not a function in the classical sense, its graph cannot be constructed in a standard way; therefore, we will do it manually, using the standard outline:

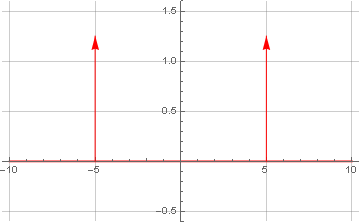
Expectedly, we received the same frequency as in the initial formula. The presence of another one of the same frequency, but with a minus sign, is not accidental - this phenomenon is calledHermitian symmetry is a consequence of the fact that the considered function is purely real and has a zero imaginary component in the complex representation. The absence of imaginary components in the spectrum after the transformation is due to the fact that initially our functions are also even (symmetric about zero).
Now let's do the Fourier transform for the signal itself:



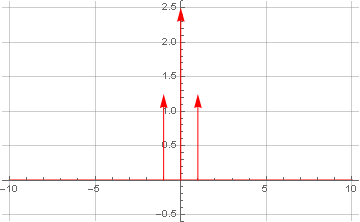
Here we additionally obtained the Dirac delta function in the center of coordinates - due to the presence of a constant component in the signal, which has no oscillations by definition - which allows it to be considered as zero frequency.
What will happen to the spectrum if they are multiplied? We'll see:



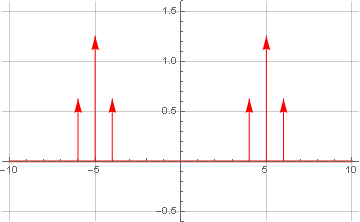
From theory we know that multiplication in the time domain is equivalent to convolution in the frequency domain (and vice versa, which is widely used in FIR filtering). And since one of the signals being convolved consisted of only one (positive and negative) frequency, as a result of the convolution, we received just a linear signal transfer upwards in frequency (in both directions). And since the symmetry remained, the signal, as before, has no imaginary component.
We now bring it to a complex ( analytical ) form, nulling the negative frequency range:

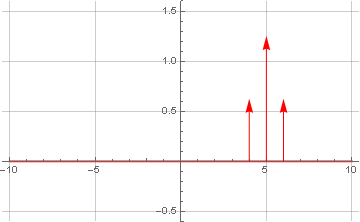
and doing the inverse Fourier transform:


Since the function is now complex, to construct its graph, you must separately extract the real and imaginary components:

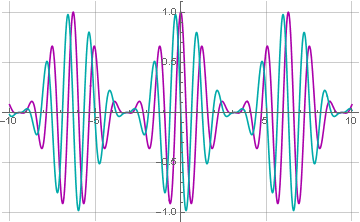
Now our signal has an imaginary component, which is the original signal shifted by 90 degrees. This will be more obvious if we present the obtained function in the trigonometric form:

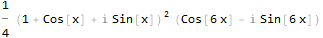
It is not very obvious yet. Let's try to simplify:

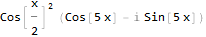
Now it looks more like the truth - and as we can see, the function of our original signal is also simplified. Let's try to return it to the original form:
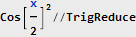

The factor 1/2 did not appear by chance - after zeroing half of the spectrum, we respectively reduced the signal power. And now, having a modulated complex signal, we can take and calculate this module:

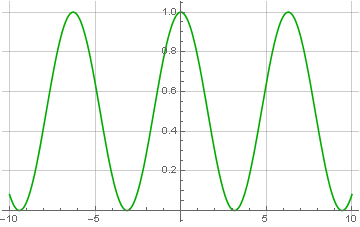
The module of a complex number is just calculated through the root of the sum of squares of the imaginary and real components. Hence, it is clear why the encoded signal should consist only of positive values — if it includes negative values, they will also become positive after restoration, which is called overmodulation:

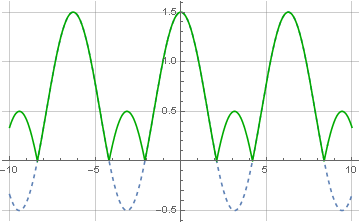
Signal recovery is also possible with the help of quadrature local oscillator — when the modulated signal is again multiplied by carrier frequency, but this time - complex:





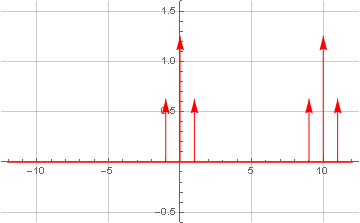
Due to the fact that the complex frequency in the frequency domain has only one pulse without duplicating it in the negative frequency range, as a result of convolution, we get a linear spectrum transfer, in which the negative part of the spectrum rises back to the center, and the positive part moves further, and it will only filter the low pass filter.
As you can see, there is nothing complicated in considering amplitude modulation through the Fourier transform; but if we consider it exclusively at the school level, then it suffices to recall that the product (carrier) of the sum (signal representation in the form of a trigonometric series) is equivalent to the sum of works (each member of the series separately on the carrier frequency) - and, accordingly, each such product is expanded into the sum of two sinusoids according to the formula already stated by the author of the original article.
The attentive reader could also notice that since the modulation resulted in a spectrum that is symmetric with respect to the carrier frequency, this means that there is data redundancy and you can leave only one sideband, thereby reducing the occupied frequency band on the radio. This technology is really available.but this is a completely different story.
So, the idea of amplitude modulation is to transmit a low-frequency signal — voice or music — by modulating a high-frequency (carrier) signal that is many times larger than the audible range and occupies a narrow frequency band on the radio. The modulation itself is performed by simply multiplying the signal by the carrier:


Here we have as a carrier a sinusoid with a frequency of 5:


And the signal itself - with a frequency of 1:


You can see that the signal is shifted up and has only positive values. This is not accidental and is a prerequisite for the possibility of its subsequent correct recovery. How to restore it? Very simple! It is necessary to shift the phase of the modulated signal by 90 degrees (an operation known as the Hilbert transform ) and calculate the root of the sum of squares of the modulated and transformed signals:


In a simpler (but coarse) version, the Hilbert transform can be replaced by a one-quarter delay in the carrier frequency, and the resulting signal can be additionally filtered out with a low-pass filter. In an even simpler version, it is possible not to count the roots and squares at all, but to filter the signal by absolute value (which is usually used in radio receivers).
Now let's see what happens with the spectra. We calculate the Fourier transform of the carrier:


Since the Dirac's delta function is not a function in the classical sense, its graph cannot be constructed in a standard way; therefore, we will do it manually, using the standard outline:


Expectedly, we received the same frequency as in the initial formula. The presence of another one of the same frequency, but with a minus sign, is not accidental - this phenomenon is calledHermitian symmetry is a consequence of the fact that the considered function is purely real and has a zero imaginary component in the complex representation. The absence of imaginary components in the spectrum after the transformation is due to the fact that initially our functions are also even (symmetric about zero).
Now let's do the Fourier transform for the signal itself:




Here we additionally obtained the Dirac delta function in the center of coordinates - due to the presence of a constant component in the signal, which has no oscillations by definition - which allows it to be considered as zero frequency.
What will happen to the spectrum if they are multiplied? We'll see:




From theory we know that multiplication in the time domain is equivalent to convolution in the frequency domain (and vice versa, which is widely used in FIR filtering). And since one of the signals being convolved consisted of only one (positive and negative) frequency, as a result of the convolution, we received just a linear signal transfer upwards in frequency (in both directions). And since the symmetry remained, the signal, as before, has no imaginary component.
We now bring it to a complex ( analytical ) form, nulling the negative frequency range:


and doing the inverse Fourier transform:


Since the function is now complex, to construct its graph, you must separately extract the real and imaginary components:


Now our signal has an imaginary component, which is the original signal shifted by 90 degrees. This will be more obvious if we present the obtained function in the trigonometric form:

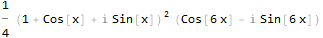
It is not very obvious yet. Let's try to simplify:

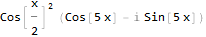
Now it looks more like the truth - and as we can see, the function of our original signal is also simplified. Let's try to return it to the original form:


The factor 1/2 did not appear by chance - after zeroing half of the spectrum, we respectively reduced the signal power. And now, having a modulated complex signal, we can take and calculate this module:


The module of a complex number is just calculated through the root of the sum of squares of the imaginary and real components. Hence, it is clear why the encoded signal should consist only of positive values — if it includes negative values, they will also become positive after restoration, which is called overmodulation:


Signal recovery is also possible with the help of quadrature local oscillator — when the modulated signal is again multiplied by carrier frequency, but this time - complex:






Due to the fact that the complex frequency in the frequency domain has only one pulse without duplicating it in the negative frequency range, as a result of convolution, we get a linear spectrum transfer, in which the negative part of the spectrum rises back to the center, and the positive part moves further, and it will only filter the low pass filter.
Conclusion
As you can see, there is nothing complicated in considering amplitude modulation through the Fourier transform; but if we consider it exclusively at the school level, then it suffices to recall that the product (carrier) of the sum (signal representation in the form of a trigonometric series) is equivalent to the sum of works (each member of the series separately on the carrier frequency) - and, accordingly, each such product is expanded into the sum of two sinusoids according to the formula already stated by the author of the original article.
The attentive reader could also notice that since the modulation resulted in a spectrum that is symmetric with respect to the carrier frequency, this means that there is data redundancy and you can leave only one sideband, thereby reducing the occupied frequency band on the radio. This technology is really available.but this is a completely different story.
