Part number 4. Folding bio-calculations. How to evaluate the folding of single-stranded RNA?
So, if you’re not tired of the “Hello, RNA World” cycle yet - catch the last article of the season :)
In the last article I justified why you should (or at least make sense) refuse to evaluate energy as an objective function. If someone is not in the know, the objective function is such a function that we invented by which we can evaluate whether we are approaching our goal or not, i.e. RNA folds “correctly” or not.
If energy is not a representative target, then what more stably / clearly indicates where to move? If we had an absolutely formalized and precise goal, this would already mean that we had solved the problem, because the formalization of the objective function itself is nothing more than a complete understanding of the process.
But we do not have such luxury. First, we are compelled to put forward a hypothesis - to what laws the process obeys, and in a certain way reflect this in the objective function.
Once again about energy as a target function - in Rosseta @ home for RNA, it was such
SCORE = (VDW * 3.0 + RG) + (RNA_BS + RNA_BP_W + RNA_BP_H + RNA_BP_S) + (RNA_NONB * 1.5 + RNA_O2ST + RNA_PHOS) + ( RNA_AXIS * 0.2 + RNA_STAG * 0.5)
I will not decrypt. But it is important that this is a certain sum of the contributions of the various alleged current impacts. The result is something arithmetic mean. And accordingly, we are moving to something amorphous. Nobody will give exact coefficients with parameters, what contribution this or that parameter makes. But it is impossible to calculate them - we are building the objective function. Guessing is also not the case. At first I tried - and I found out that a large half simply does not make a serious contribution, but only rejects the calculations in the wrong place.
Therefore, at the beginning I left only VDW - this is a kind of generalized coefficient, in fact it shows whether there are forbidden covalent bonds (which was discussed in the first articles). And over time, I replaced it simply with a yes / no answer, because it happened that other parameters - sometimes outweighed - and as a result, intersections in the .pdb file turned out, which should not be.
Further, we remember that I proposed to rely only on the formation of hydrogen bonds. When they are formed, we mathematically know without any far-fetched things: distance and angle are everything. Where in RNA they are - we also know stably. (more precisely, it is now fairly well predicted, there are nuances - but then).
In the figure, the secondary structure of one ribozyme, which I took for experiments
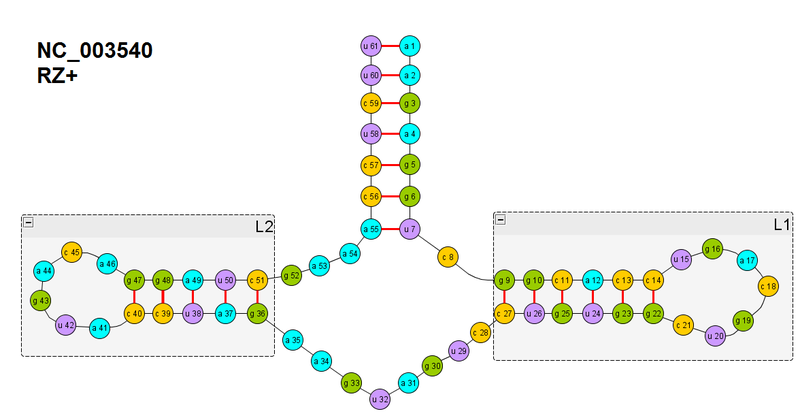
in order to simplify my life, I started with the already existing hypothesis that RNA / proteins fold hierarchically: the so-called The Hierarchical model, which has a number of variations, but the essence is this: first , elements of the secondary structure in the expanded chain begin to form. If we focus on the word “start”, then this is a completely normal hypothesis, but sometimes it is understood that secondary structures are fully formed, and only then further folding occurs. This is somewhat incorrect. But this will be important to us later, when we are folding the ribozyme completely (I’ll say right away, I still haven’t succeeded - according to my criteria, but they turned out to be tougher, because I’m not basing on energy, where the minimum is not clearly reached or it is possible even better But I seem to be close to the solution.).
Now, let's collapse at least a small area, form hydrogen bonds between two nucleotides. Take the right loop of cugacgucg (from 14 to 22) - 9 nucleotides and form a hydrogen bond between the extreme cg.
How to build an objective function?
There are 3 hydrogen bonds between cg, so we have three distances (r1, r2, r3) and three angles (a1, a2, a3). For the function to be speaking, we need it to be like this: if its value is ultimately zero or less, then all 3 hydrogen bonds have formed. A positive value should smoothly show the approach to this state.
Therefore, it is necessary to subtract 3 agstroms from current distances, and 20 degrees from angles. We get the values that make a positive contribution to the function. I would like to add all these 3 angles and 3 distances - and we get the value of the objective function. But the distances and angles to pry lightly - different values. Therefore, there is such a method of bringing to one scale. Significant distances (after subtracting 3) we have somewhere from 1 to 12. Significant in the sense that the angle already affects these distances. And if the distance is greater, then the angle is not important: what's the difference how the atoms are rotated, if they are separated by an abyss. And the angles we have are from 0 to 180, minus 20 = 160.
If you roughly estimate it turns out that if you multiply the distance by 10, then the distances and angles will be on the same scale. Therefore, we do:
r1 - = 3.0f; r1 * = 10;
r2 - = 3.0f; r2 * = 10;
r3 - = 3.0f; r3 * = 10;
a1 - = 20;
a2 - = 20;
a3 - = 20;
There are two options. One
locScore = (r1 + r2 + r3 + a1 + a2 + a3)
and the second
if (maxR> maxA)
{locScore = maxR; }
else
{locScore = maxA; }
where maxR = maximum from (r1, r2, r3), and maxA = maximum from (a1, a2, a3)
Each of the options is good in its own way. To start folding, the second is good. After having already a rough structure, the first one may come in handy.
Well, the algorithm is very simple: we start to rotate (in part No. 3 - remember that 1500 possible turns were selected) nucleotides with numbers
14
15
16
17
18 - for example, it’s here that the turn with the number 210 is the best among all
19
20
21
22 we
rotate, say, at two angles No. 1 and No. 6 (ie No. 16). Finding the best fix. Our little chain will fold in two. After some time, we drive into the “voltage” (the ends of the left and right tend to connect, and the loop is subjected to tension) so that our circuit stops at angles 1 and 6 and the algorithm goes in cycles. As soon as he ceases to give the best condition, we change the combination of angles, for example, 3 and 4 (No. 34), etc. This will gradually unload the voltage at angles 1 and 6, and then you can still try to “compress” them.
This algorithm is quite enough for the required hydrogen bond to form.
In the next article of the second season :) we will talk about the difficulties that arise when the whole spiral is formed. But still one spiral.
PS I am very glad that serious comments appeared on the third article. But at the same time, it seems like a layman, a potential FoldIt player or just supporting bio. distributed computing - lose interest. Some completed part (Hello, RNA World) I told. It will not be any more complicated, but perhaps the details of the rest are not so interesting for the townsfolk (write if this is not so). I do not hide the fact that I am looking for like-minded people and those with whom I can test hypotheses, but at the same time I'm not ready for mass production, and the software is not ready either. In general, who cares, write, then I will ripen faster for season number two.
An important question for mathematicians :
I described two objective functions
above 1. locScore = (r1 + r2 + r3 + a1 + a2 + a3)
2. if (maxR> maxA) {locScore = maxR; } else {locScore = maxA; }
Do you know how to combine them into one? Those. let's say if the first objective function was used 5 times, then the second one was applied 5 times and we got a certain result (lowering the “energy”). It is necessary that the function obtained after combining, after its application 5 times, would give the same result as if you apply the first and second in turn. Is it possible?
In the last article I justified why you should (or at least make sense) refuse to evaluate energy as an objective function. If someone is not in the know, the objective function is such a function that we invented by which we can evaluate whether we are approaching our goal or not, i.e. RNA folds “correctly” or not.
If energy is not a representative target, then what more stably / clearly indicates where to move? If we had an absolutely formalized and precise goal, this would already mean that we had solved the problem, because the formalization of the objective function itself is nothing more than a complete understanding of the process.
But we do not have such luxury. First, we are compelled to put forward a hypothesis - to what laws the process obeys, and in a certain way reflect this in the objective function.
Once again about energy as a target function - in Rosseta @ home for RNA, it was such
SCORE = (VDW * 3.0 + RG) + (RNA_BS + RNA_BP_W + RNA_BP_H + RNA_BP_S) + (RNA_NONB * 1.5 + RNA_O2ST + RNA_PHOS) + ( RNA_AXIS * 0.2 + RNA_STAG * 0.5)
I will not decrypt. But it is important that this is a certain sum of the contributions of the various alleged current impacts. The result is something arithmetic mean. And accordingly, we are moving to something amorphous. Nobody will give exact coefficients with parameters, what contribution this or that parameter makes. But it is impossible to calculate them - we are building the objective function. Guessing is also not the case. At first I tried - and I found out that a large half simply does not make a serious contribution, but only rejects the calculations in the wrong place.
Therefore, at the beginning I left only VDW - this is a kind of generalized coefficient, in fact it shows whether there are forbidden covalent bonds (which was discussed in the first articles). And over time, I replaced it simply with a yes / no answer, because it happened that other parameters - sometimes outweighed - and as a result, intersections in the .pdb file turned out, which should not be.
Further, we remember that I proposed to rely only on the formation of hydrogen bonds. When they are formed, we mathematically know without any far-fetched things: distance and angle are everything. Where in RNA they are - we also know stably. (more precisely, it is now fairly well predicted, there are nuances - but then).
In the figure, the secondary structure of one ribozyme, which I took for experiments

in order to simplify my life, I started with the already existing hypothesis that RNA / proteins fold hierarchically: the so-called The Hierarchical model, which has a number of variations, but the essence is this: first , elements of the secondary structure in the expanded chain begin to form. If we focus on the word “start”, then this is a completely normal hypothesis, but sometimes it is understood that secondary structures are fully formed, and only then further folding occurs. This is somewhat incorrect. But this will be important to us later, when we are folding the ribozyme completely (I’ll say right away, I still haven’t succeeded - according to my criteria, but they turned out to be tougher, because I’m not basing on energy, where the minimum is not clearly reached or it is possible even better But I seem to be close to the solution.).
Now, let's collapse at least a small area, form hydrogen bonds between two nucleotides. Take the right loop of cugacgucg (from 14 to 22) - 9 nucleotides and form a hydrogen bond between the extreme cg.
How to build an objective function?
There are 3 hydrogen bonds between cg, so we have three distances (r1, r2, r3) and three angles (a1, a2, a3). For the function to be speaking, we need it to be like this: if its value is ultimately zero or less, then all 3 hydrogen bonds have formed. A positive value should smoothly show the approach to this state.
Therefore, it is necessary to subtract 3 agstroms from current distances, and 20 degrees from angles. We get the values that make a positive contribution to the function. I would like to add all these 3 angles and 3 distances - and we get the value of the objective function. But the distances and angles to pry lightly - different values. Therefore, there is such a method of bringing to one scale. Significant distances (after subtracting 3) we have somewhere from 1 to 12. Significant in the sense that the angle already affects these distances. And if the distance is greater, then the angle is not important: what's the difference how the atoms are rotated, if they are separated by an abyss. And the angles we have are from 0 to 180, minus 20 = 160.
If you roughly estimate it turns out that if you multiply the distance by 10, then the distances and angles will be on the same scale. Therefore, we do:
r1 - = 3.0f; r1 * = 10;
r2 - = 3.0f; r2 * = 10;
r3 - = 3.0f; r3 * = 10;
a1 - = 20;
a2 - = 20;
a3 - = 20;
There are two options. One
locScore = (r1 + r2 + r3 + a1 + a2 + a3)
and the second
if (maxR> maxA)
{locScore = maxR; }
else
{locScore = maxA; }
where maxR = maximum from (r1, r2, r3), and maxA = maximum from (a1, a2, a3)
Each of the options is good in its own way. To start folding, the second is good. After having already a rough structure, the first one may come in handy.
Well, the algorithm is very simple: we start to rotate (in part No. 3 - remember that 1500 possible turns were selected) nucleotides with numbers
14
15
16
17
18 - for example, it’s here that the turn with the number 210 is the best among all
19
20
21
22 we
rotate, say, at two angles No. 1 and No. 6 (ie No. 16). Finding the best fix. Our little chain will fold in two. After some time, we drive into the “voltage” (the ends of the left and right tend to connect, and the loop is subjected to tension) so that our circuit stops at angles 1 and 6 and the algorithm goes in cycles. As soon as he ceases to give the best condition, we change the combination of angles, for example, 3 and 4 (No. 34), etc. This will gradually unload the voltage at angles 1 and 6, and then you can still try to “compress” them.
This algorithm is quite enough for the required hydrogen bond to form.
In the next article of the second season :) we will talk about the difficulties that arise when the whole spiral is formed. But still one spiral.
PS I am very glad that serious comments appeared on the third article. But at the same time, it seems like a layman, a potential FoldIt player or just supporting bio. distributed computing - lose interest. Some completed part (Hello, RNA World) I told. It will not be any more complicated, but perhaps the details of the rest are not so interesting for the townsfolk (write if this is not so). I do not hide the fact that I am looking for like-minded people and those with whom I can test hypotheses, but at the same time I'm not ready for mass production, and the software is not ready either. In general, who cares, write, then I will ripen faster for season number two.
An important question for mathematicians :
I described two objective functions
above 1. locScore = (r1 + r2 + r3 + a1 + a2 + a3)
2. if (maxR> maxA) {locScore = maxR; } else {locScore = maxA; }
Do you know how to combine them into one? Those. let's say if the first objective function was used 5 times, then the second one was applied 5 times and we got a certain result (lowering the “energy”). It is necessary that the function obtained after combining, after its application 5 times, would give the same result as if you apply the first and second in turn. Is it possible?
