Recursive functions - creating your own math (Scala)

Good afternoon, Habr!

With this pretentious title, I want to start an article about one of the many calculus models (recutational model) - recursive functions . In the first part of this post we will analyze (in short, because everything is detailed on Wikipedia) the theoretical component of this model (primitive recursion), in the second half we will try to implement this model (partially) using the Scala language.

1. Recursive functions - what is it?

Everyone knows the phrase “Turing Machine” - a calculus model created by a British mathematician, logician, cryptographer and just a good person Alan Turing . This model is one of the most famous and popular calculus models among many . However, recently other models such as lambda calculus and mu recursion have begun to become popular.

And yet, what is a recursive function?
Imagine that in front of you lies an abstract computer that does not know (yet) such operations as adding two numbers, subtracting, differentiating and integrating. How to work with such a machine? How to teach her to count?
To begin with, we define the basic functionality that this machine should have:

• A set of basic mathematical functions:
  
  - Zero (x) = 0: for each given argument x, the function returns 0
  
  - Succ (x) = x + 1: for each given x, the function returns x + 1
  
  - The family of projection functions , where 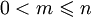: for any n The argument returns the one that stands at m position.
  
• The set of operations that we can apply to these functions:
  
  - Composition of functions (superposition): (f • g) (x) = f (g (x));
  
  - Primitive recursion: Let there be a function f (x1, x2, ..., xn) of n variables, and a function g (X1, X2, ..., Xn, Xn + 1, Xn + 2) of n + 2 variables . Then we can define the function h (X1, X2, .... Xn, Xn + 1) of n + 1 variables:
  
  h (X1, X2, ..., Xn, 0) = f (X1, X2, .. ., Xn);
  h (X1, X2, ..., Xn, i + 1) = g (X1, X2, ..., Xn, i, h (X1, X2, ..., Xn, i));
  

That's all that our abstract computer can do. The main thing on this list, you guessed it, is primitive recursion. To make it clearer, we set ourselves the task, for example, to implement the function of adding two numbers a and b:

Sum (a, b):
Sum (a, 0) = I (a);
Sum (a, i + 1) = Succ (F (a, i, Sum (a, i))) where F is the projection of the third argument, that is, in this case F will return Sum (a, i);

All! Now we can add two numbers and we are very happy about this.
By the way, maybe someone has a question, why is it so difficult to paint Sum (a, i + 1), and why not just write Sum (a, i + 1) = Succ (Sum (a, i)). I answer: by definition, a recursive function must have as arguments all the arguments (except for the iterative) of the desired function (in our case it is a), also the iterative argument reduced by one (in our case it is i), and actually the recursive call Sum (a , i). This is done in order to be able to work with non-primitive recursion (iteration follows two or more arguments).

As you understand, in the same way we can create a function of inhibition, degree, etc. All these examples are very well painted on Wikipedia, and we will implement them in the second part of the article. In any case, we can already define an infinite set of primitive recursive functions:

F = {f0, f1, f2, f3, ...} is an infinite countable set of functions defined as follows:

f0 (0, y) = Succ (y);
f [n + 1] (x, y): f [n + 1] (0, y) = y; f [n + 1] (i + 1, y) = fn (y, f [n + 1] (i, y));

This is primitive recursion.
I won’t dive deeper and tell what μ-recursive function is , everything is very nicely painted on Wikipedia, especially since primitive recursion is enough for us to start implementing our own ... math!

2. Primitive recursion on Scala

First, we need to determine what a number is? Create an abstract class MyNumber:

abstract class MyNumber {
  val isNatural: Boolean
  val isNeg: Boolean
  val isZero: Boolean
  val isInf: Boolean
  def +(b: MyNumber): MyNumber
  def -(b: MyNumber): MyNumber
  def *(b: MyNumber): MyNumber
  def /(b: MyNumber): MyNumber
  def ^(b: MyNumber): MyNumber
  def <(b: MyNumber): Boolean
  def >(b: MyNumber): Boolean
  def ==(b: MyNumber): Boolean
  def neg: MyNumber
  def abs: MyNumber
  def pre: MyInteger
  def suc: MyInteger
  val num: MyInteger
  val denum: MyInteger
  def gcd(b: MyNumber): MyNumber  
  def mod(b: MyInteger): MyNumber
  override def toString(): String
  def toInteger: MyInteger =
    if(isNatural) this.asInstanceOf[MyInteger]
    else (num / denum).asInstanceOf[MyInteger]
  def toFraction: Fraction = 
    if(isNatural) new Fraction(this.toInteger)
    else this.asInstanceOf[Fraction]
}

As already seen, we will have two child classes, Fraction and MyInteger:

abstract class MyInteger extends MyNumber {
  val isNatural = true
  val isNeg: Boolean
  val isZero: Boolean
  val isInf: Boolean
  def +(b: MyNumber): MyNumber =
    if (b.isNatural) this plusInt b.toInteger
    else this plusFrac b.toFraction
  protected def plusInt(b: MyInteger): MyNumber
  private def plusFrac(b: Fraction): MyNumber = this.toFraction + b
  def -(b: MyNumber): MyNumber =
    if (b.isNatural) this minusInt b.toInteger
    else this minusFrac b.toFraction
  protected def minusInt(b: MyInteger): MyNumber
  private def minusFrac(b: Fraction): MyNumber = this.toFraction - b
  def *(b: MyNumber): MyNumber =
    if (b.isNatural) this multInt b.toInteger
    else this multFrac b.toFraction
  protected def multInt(b: MyInteger): MyNumber
  private def multFrac(b: Fraction): MyNumber = this.toFraction * b
  def /(b: MyNumber): MyNumber =
    if (b.isNatural) this divInt b.toInteger
    else this divFrac b.toFraction
  protected def divInt(b: MyInteger): MyNumber
  private def divFrac(b: Fraction): MyNumber = this.toFraction / b
  def ^(b: MyNumber): MyNumber =
    if (b.isNatural) this powInt b.toInteger
    else this powFrac b.toFraction
  protected def powInt(b: MyInteger): MyNumber
  protected def powFrac(b: Fraction): MyNumber //TODO
  def <(b: MyNumber): Boolean =
    if (b.isNatural) this lessThanInt b.toInteger
    else this lessThanFrac b.toFraction
  protected def lessThanInt(b: MyInteger): Boolean
  private def lessThanFrac(b: Fraction): Boolean = this.toFraction < b
  def >(b: MyNumber): Boolean =
    if (b.isNatural) this biggerThanInt b.toInteger
    else this biggerThanFrac b.toFraction
  protected def biggerThanInt(b: MyInteger): Boolean
  private def biggerThanFrac(b: Fraction): Boolean = this.toFraction > b
  def ==(b: MyNumber): Boolean =
    if (b.isNatural) this equalsInt b.toInteger
    else this equalsFrac b.toFraction
  protected def equalsInt(b: MyInteger): Boolean
  private def equalsFrac(b: Fraction): Boolean = this.toFraction == b
  def pre: MyInteger
  def suc: MyInteger
  val num: MyInteger = null
  val denum: MyInteger = null
  def neg: MyNumber
  def abs: MyNumber =
    if (!isNeg || isZero) this
    else this neg
  def gcd(b: MyNumber): MyNumber =
    if (b.isNatural) this gcdPrivate b.abs.toInteger
    else (new Zero).pre
  private def gcdPrivate(b: MyNumber): MyNumber = {
      def iter(a: MyNumber, b: MyNumber): MyNumber = {
        if (b == (new Zero)) a else iter(b, a.toInteger mod b.toInteger)
      }
    iter(this, b)
  }
  def mod(b: MyInteger): MyNumber = {
      def iter(a: MyNumber, b: MyNumber): MyNumber = {
        if (b.isNeg) this mod b.abs.toInteger
        else if (!b.isNatural) (new Zero).pre
        else if (a < b) if (a.isNeg) a + b else a
        else iter(if (a.isNeg) a + b else a - b, b)
      }
    iter(this, b)
  }
  override def toString: String = {
      def iter(nb: MyInteger, accu: Int): Int = {
        if (nb isZero) accu
        else if (nb isNeg) iter(nb.suc.toInteger, accu - 1)
        else iter(nb.pre.toInteger, accu + 1)
      }
    if(this.isInf) "Inf" else iter(this, 0).toString()
  }
}

To define Integer, we need the concept of the following number (Suc), previous (Pre), zero (Zero) and infinity (PosInf):

class Zero extends MyInteger {
  val isZero = true
  val isNeg = false
  val isInf = false
  protected def plusInt(b: MyInteger): MyNumber = b
  protected def minusInt(b: MyInteger): MyNumber = b neg
  protected def multInt(b: MyInteger): MyNumber = this
  protected def divInt(b: MyInteger): MyNumber =
    if (b.isZero) new PosInf
    else if(b.isInf) new Zero
    else this
  protected def powInt(b: MyInteger): MyNumber = this.suc
  protected def powFrac(b: Fraction): MyNumber = this.suc
  protected def lessThanInt(b: MyInteger): Boolean = !b.isNeg && !b.isZero
  protected def biggerThanInt(b: MyInteger): Boolean = b.isNeg && !b.isZero
  protected def equalsInt(b: MyInteger): Boolean = b.isZero
  def pre: MyInteger = new Pre(this)
  def suc: MyInteger = new Suc(this)
  def neg = this
}
class PosInf extends MyInteger {
  val isZero = false
  val isNeg = false
  val isInf = true
  protected def plusInt(b: MyInteger): MyNumber = this
  protected def minusInt(b: MyInteger): MyNumber = this
  protected def multInt(b: MyInteger): MyNumber = this
  protected def divInt(b: MyInteger): MyNumber = this
  protected def powInt(b: MyInteger): MyNumber = this
  protected def powFrac(b: Fraction): MyNumber = this
  protected def lessThanInt(b: MyInteger): Boolean = false
  protected def biggerThanInt(b: MyInteger): Boolean = true
  protected def equalsInt(b: MyInteger): Boolean = b.isInf
  def pre: MyInteger = this
  def suc: MyInteger = this
  def neg = this
}
class Pre(nb: MyInteger) extends MyInteger {
  val isZero = false
  val isNeg = true
  val isInf = false
  protected def plusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) this - (b neg)
        else if (b isZero) accu
        else iter(b.pre, accu.suc)
      }
    iter(b, this)
  }
  protected def minusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) (this + (b neg))
        else if (b isZero) accu
        else iter(b.pre, accu.pre)
      }
    iter(b, this)
  }
  protected def multInt(b: MyInteger): MyNumber = {
    (this.neg * b).neg
  }
  protected def divInt(b: MyInteger): MyNumber =
    if (b.isZero) new PosInf
    else if(b.isInf) new Zero
    else if (b.isNeg) this.abs / b.abs
    else (this.abs / b).neg
  protected def powInt(b: MyInteger): MyNumber = if(b!=new Zero)(this.neg ^ b).neg else (new Zero).suc
  protected def powFrac(b: Fraction): MyNumber = (new Zero).pre //TODO
  protected def lessThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => !(a isZero) && (b isZero)
        case false => iter(a.suc, b.suc)
      }
    if (!b.isNeg || b.isZero) true else iter(this, b)
  }
  protected def biggerThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => (a isZero) && !(b isZero)
        case false => iter(a.suc, b.suc)
      }
    if (!b.isNeg || b.isZero) false else iter(this, b)
  }
  protected def equalsInt(b: MyInteger): Boolean = !(this < b) && !(this > b)
  def pre: MyInteger = new Pre(this)
  def suc: MyInteger = nb
  def neg = {
      def iter(nb: MyInteger, accu: MyInteger): MyInteger = {
        if (nb isZero) accu
        else iter(nb.suc, accu.suc)
      }
    iter(this, new Zero)
  }
}
class Suc(nb: MyInteger) extends MyInteger {
  val isZero = false
  val isNeg = false
  val isInf = false
  protected def plusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) this - (b neg)
        else if (b isZero) accu
        else iter(b.pre, accu.suc)
      }
    iter(this, b)
  }
  protected def minusInt(b: MyInteger): MyNumber = {
      def iter(b: MyInteger, accu: MyNumber): MyNumber = {
        if (b isNeg) this + (b neg)
        else if (b isZero) accu
        else iter(b.pre, accu.pre)
      }
    iter(b, this)
  }
  protected def multInt(b: MyInteger): MyNumber = {
      def iter(a: MyInteger, b: MyInteger, accu: MyNumber): MyNumber = {
        if (b.isZero) accu
        else iter(a, b.pre, accu + a)
      }
    if (b.isZero) new Zero
    else {
      if (this < b) {
        if (b.isNeg) iter(b.neg.toInteger, this, new Zero).neg
        else iter(b, this, new Zero)
      } else {
        if (b.isNeg) iter(this, b.neg.toInteger, new Zero).neg
        else iter(this, b, new Zero)
      }
    }
  }
  protected def divInt(b: MyInteger): MyNumber = {
      def iter(a: MyNumber, b: MyNumber, count: MyNumber): MyNumber = {
        if (a.isZero) count
        else if (a.isNeg) count.pre
        else iter(a - b, b, count.suc)
      }
    if (b.isZero) new PosInf
    else if(b.isInf) new Zero
    else if (b.isNeg) iter(this, b.abs, new Zero).neg
    else iter(this, b, new Zero)
  }
  protected def powInt(b: MyInteger): MyNumber = {
      def iter(a: MyInteger, b: MyInteger, accu: MyNumber): MyNumber = {
        if (b.isZero) accu
        else iter(a, b.pre, accu * a)
      }
    if (b.isZero) (new Zero).suc
    else {
      if (b.isNeg) new Fraction((new Zero).suc, iter(this, b.neg.toInteger, (new Zero).suc).toInteger)
      else new Fraction(iter(b, this, (new Zero).suc).toInteger)
    }
  }
  protected def powFrac(b: Fraction): MyNumber = (new Zero).pre //TODO
  protected def lessThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => (a isZero) && !(b isZero)
        case false => iter(a.pre, b.pre)
      }
    if (b.isNeg || b.isZero) false else iter(this, b)
  }
  protected def biggerThanInt(b: MyInteger): Boolean = {
      def iter(a: MyInteger, b: MyInteger): Boolean = a.isZero || b.isZero match {
        case true  => !(a isZero) && (b isZero)
        case false => iter(a.pre, b.pre)
      }
    if (b.isNeg || b.isZero) true else iter(this, b)
  }
  protected def equalsInt(b: MyInteger): Boolean = !(this < b) && !(this > b)
  def pre: MyInteger = nb
  def suc: MyInteger = new Suc(this)
  def neg = {
      def iter(nb: MyInteger, accu: MyInteger): MyInteger = {
        if (nb isZero) accu
        else iter(nb.pre, accu.pre)
      }
    iter(this, new Zero)
  }
}

The Fraction class is somewhat easier, because it is completely based on MyInteger:

class Fraction(x: MyInteger, y: MyInteger) extends MyNumber {
  def this(x: MyInteger) = this(x, (new Zero).suc)
  val isNatural: Boolean = false
  val isNeg: Boolean = (x.isNeg && !y.isNeg) || (!x.isNeg && y.isNeg)
  val isZero: Boolean = x.isZero
  val isInf: Boolean = x.isInf || y.isInf
  def +(b: MyNumber): MyNumber = this plus b.toFraction
  private def plus(b: Fraction): MyNumber = new Fraction((this.num * b.denum + this.denum * b.num).toInteger, (this.denum * b.denum).toInteger)
  def -(b: MyNumber): MyNumber = this minus b.toFraction
  private def minus(b: Fraction): MyNumber = new Fraction((this.num * b.denum - this.denum * b.num).toInteger, (this.denum * b.denum).toInteger)
  def *(b: MyNumber): MyNumber = this mult b.toFraction
  private def mult(b: Fraction): MyNumber = new Fraction((this.num * b.num).toInteger, (this.denum * b.denum).toInteger)
  def /(b: MyNumber): MyNumber = this div b.toFraction
  private def div(b: Fraction): MyNumber = new Fraction((this.num * b.denum).toInteger, (this.denum * b.num).toInteger)
  def ^(b: MyNumber): MyNumber =
    if (!b.isNatural) (new Zero).pre
    else new Fraction((this.num ^ b.toInteger).toInteger, (this.denum ^ b.toInteger).toInteger)
  def <(b: MyNumber): Boolean =
    if (this.num.isNeg) {
      if (b.num.isNeg) this.neg > b.neg
      else true
    } else if (this.isZero) {
      if (b.isZero || b.num.isNeg) false
      else true
    } else {
      if (b.num.isNeg || b.isZero) false
      else this.num * b.denum < this.denum * b.num
    }
  def >(b: MyNumber): Boolean =
    if(this.num.isNeg){
      if(b.num.isNeg) this.neg < b.neg
      else false
    }else if(this.isZero){
      if(b.isZero || !b.num.isNeg) false
      else true
    }else{
      if(b.num.isNeg || b.isZero) true
      else this.num * b.denum > this.denum * b.num
    }
  def ==(b: MyNumber): Boolean =
    if(!b.isNatural)(this.num == b.num) && (this.denum == b.denum)
    else this == b.toFraction
  def neg: MyNumber = new Fraction(num.neg.toInteger, denum)
  def abs: MyNumber = new Fraction(num.abs.toInteger, denum)
  def pre: MyInteger = sys.error("Predicat of fraction")
  def suc: MyInteger = sys.error("Successor of fraction")
  val num = ((if(this.isNeg)x.abs.neg else x.abs) / (x.abs gcd y.abs)).toInteger
  val denum = (y.abs / (x.abs gcd y.abs)).toInteger
  def gcd(b: MyNumber): MyNumber = this.denum gcd (new Zero).suc
  def mod(b: MyInteger): MyNumber = new Zero
  override def toString(): String =
    if(num.isZero) 0.toString()
    else if(this.isInf) "вИЮ"
    else if(denum == (new Zero).suc) num.toString()
    else num + "/" + denum
}

That's all! We now have natural and fractional numbers, and a set of simple operations (mind you, not a single use of native classes!) Using

the same principle, you can create data structures for newly appeared numbers:

abstract class MySet {
  def add(elem: MyNumber): MySet
  def delete(elem: MyNumber): MySet
  def union(set: MySet): MySet
  def intersec(set: MySet): MySet
  def contains(elem: MyNumber): Boolean
  def linearSearch(elem: MyNumber): MySet
  def mergeSort: MySet
  def merge: MySet
  def quickSort: MySet
  def timSort: MySet
  def binaryTreeSort: MySet
  def length: MyNumber
  def get(pos: MyNumber): MyNumber
  def take(n: MyNumber): MySet
  def drop(n: MyNumber): MySet
  def map(p: MyNumber => MyNumber): MySet
  def filter(p: MyNumber => Boolean): MySet
  def flat(p: (MyNumber, MyNumber) => MyNumber): MyNumber

Yes, and a lot of things can be done with recursive functions, even creating your own universe. "With blackjack and whores." Thanks for attention.