Richard Hamming: Chapter 17. Digital Filters - IV

“The goal of this course is to prepare you for your technical future.”

Hi, Habr. Remember the awesome article "You and your work" (+219, 2442 bookmarks, 393k reads)?

So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book based on his lectures. We translate it, because the man is talking.

This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes the conditions that increase the chances of doing a great job. ”

We have already translated 24 (out of 30) chapters. And we are working on the publication "in paper."

Chapter 17. Digital Filters - IV

(For the translation, thanks to Andrey Pakhomov, who responded to my call in the “previous chapter.”) Who wants to help with the translation, layout and publication of the book - write in a personal or mail magisterludi2016@yandex.ru

And now we turn to the recursive filters that have the following form:



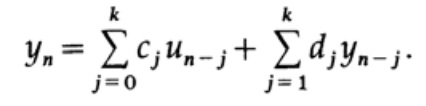
From this formula we see that we have values ​​only on one side of the current nth value. We use the previous values ​​of the signal and its value at the current time un and also the previous values ​​obtained at the output of the filter.
This classic approach is the result of the fact that we often process the signal in real time and we do not have access to future signal values.

Recalling the basics, we’ll see that if we had “future values”, it’s likely that two-way prediction would be much more accurate. Then, to calculate yn, we would encounter a system that would instantly solve linear equations — nothing terrible in the age of cheap computation.We will put aside this observation, nowadays we often write the signal to tape or other media, and later we process the data in the laboratory — and therefore we have future values ​​for some point in time. For example, using a recursive digital filter in image processing would be folly, because it does not use some of the available, relevant information.

The next aspect that needs attention when using the previous output value as the next input is the presence of feedback - and this automatically raises the issue of stability. This condition, which we must constantly monitor in the design of recursive filters. This limits what we can do. In this case, stability means that the effect of the initial conditions does not begin to prevail in the final result.

Working with a linear system, we saw that no matter what frequency we applied to the filter input, when it is in the steady state, only this frequency occurs at the filter output, although the output signal phase can be shifted relative to the original signal phase. However, in the transient state, other frequencies may appear that arise from the solution of a homogeneous differential equation. A recursive filter is nothing more than a solution to a differential equation with constant coefficients with un members forming the forcing function.

Therefore, for the stationary state (ignoring transients), we assume that



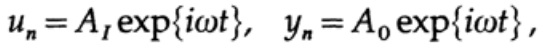
(where A can be complex numbers to take into account the phase shift), and this leads to the solution of the ratio A0 / A1 for finding the transfer function:



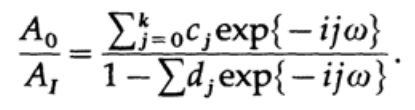
This expression is a rational function of the complex variable exp {iωt} = z, in contrast to the previously non-recursive filter, where the transfer characteristic was a polynomial in z. The theoretical part of the function representation in the form of a Fourier series expansion is developed; but so far there is no theory on the representation of a function as a relation of two Fourier series (I think that there are no reasons why there can be no such theory). Therefore, at present, the design methods are not systematic (which Kaiser did not design recursive filters for design), but rather a set of tricks.

Thus, we have a Butterworth filter, two types of Chebyshev filters (depending on the presence of the same ripple in the passbands and suppression) and an elliptic filter (which is so named because of the use of elliptic functions), which has the same ripple in both bands.



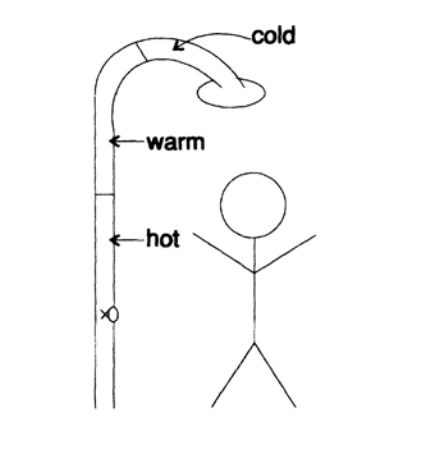
Figure 17.1

I will only touch on the topic of feedback. To make the feedback problem visual, I’ll tell you a story about me. Once upon a time, I participated in a series of six half-hour television programs on computers and computing. Filming took place mainly in San Francisco. I often stayed there and had the habit of staying in the same room in the same hotel - it’s great to know the room in all details, when it is already deep night and you are tired or when you have to get up in the middle of the night - hence the desire to stay in the same the room.

It’s great that a plumber connected a shower to large-diameter pipes (Figure 17.I). As a result, in the mornings when I started to take a shower the water was too cold, I turned the knob of the faucet with warm water more, it was still too cold, and more, it was still too cold, and even more, and finally, when the water became the right temperature i stayed Of course, the water grew hotter and hotter as the water that had previously entered the pipes went outside, and I had to jump out of the shower and try again to find the appropriate position for the handle of the hot water tap. The delay in the supply of hot water caused me inconvenience. I found myself, in spite of a wealth of experience, in a classic situation of instability. You can look at this situation from one of two sides: or my response was too strong (I was very rude in my actions) or the detection of the signal was too late (I was too quick in adjusting the tap). The same long-lasting effect! I have never had to deal with big delays before, so every day my morning began with inconvenience! In this illustrative example, you can look at the very essence of instability.

Here I will not delve into the design of recursive filters, just note that during the struggle with the correction formulas for the numerical solution of ordinary differential equations, I independently developed one theory.

The corrector in the predictor-correctors method has the form



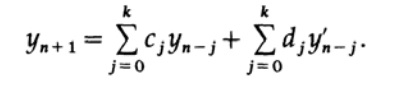
We see that now the coefficients uj of the recursive filter are the derivatives of the output of the filter yn ', which are taken from the differential equation. In conventional non-recursive filters, there is no feedback loop — the computed values ​​of yn do not appear later on the right side of the expression. In differential equations, they appear both in the feedback loop and in its derivatives, thereby forming another feedback loop, usually non-linear. Therefore, stability in the field of solving differential equations is a more complex topic than in the field of recursive filters.

Such recursive filters are often called “filters with infinite impulse response” (IIR filters), because a single perturbation will echo through the feedback loop, which will exponentially exponentially, and only if the filter is stable. I would not be myself if I had not asked myself whether all recursive filters should have this property. I soon found the opposite example. In truth, this is not the kind of filter that you will normally design, but this example shows that this statement is superficial. If you ask yourself if everything you say is true, then you will be surprised at how much everything will turn out to be false, even in well-developed areas!

In Chapter 26I will address the problem of working with experts. Now you will see an example of what happens too often. The experts were told something in the classroom when they were still students, and they didn’t ask themselves questions, they simply accepted this as a fact. And they constantly reproduce this accepted fact even without trying to check whether it is true or not, especially with reference to the problem that they are trying to solve at this moment.

Let me tell you another story now. One lady from the Mathematics Department of Laboratories Bell danced square dance with one of the physicists at the party at the weekend, and on Monday morning, she mentioned in the corridor with me about the problem he had encountered. He measured the number of pulses in a radioactive experiment on each of, as I recall, 256 energy levels. This is called the "spectrum of the process." His problem was to obtain a derivative of the data.

So, you know that (a) the number of pulses of a certain level of energy will form a curve with discontinuities and (b) differentiating it to obtain a local angular coefficient is not an easy task for itself. The more I thought about her random note, the more I felt that he needed a good assistant — that is, me! I found him in the Bell Laboratories telephone directory and explained his interest to him and how I got to him. He immediately wanted to come to my office, but I was stubborn, and insisted on meeting in his laboratory. He tried to offer his office, but I still insisted on his laboratory. What for? In order to evaluate his abilities and decide whether his problem is worth my time and effort, as she promised to be a tough nut to crack. He brilliantly passed the test laboratory - it became clear

He was almost at the limit of what he could do - data was collected during the week, and the source of radiation was hidden by a multitude of screens. It did not seem like something else could be done to collect more accurate data. Moreover, I soon became convinced, despite the fact that I knew few details that his experiment was important for physics as well as for Bell Laboratories. So, I took on this task. Moral: in some way you can choose, and work on those tasks that you think are important.

Obviously, this was a smoothing problem, and Kaiser, in fact, had just trained me, so what could be better than to lead the experimenter to Kaiser and ask Kaiser to design a suitable differentiating filter? Immediately the problems started. The Kaiser always thought of a signal as a function of time, and of the area under the curve as energy, and in this case energy was an independent variable! At this point, the problem with the Kaiser was repeated until I directly told him: “Well, his energy is time, and the measurements, impulses, this voltage”. Only after that Kaiser was able to solve the problem.

The experts curse is their limited understanding of what they can do. I mentioned to you that Kaiser is a very capable person, but his experience, as often happens with experts, limited his vision. Can you in turn do better? I hope these stories will help you avoid this trap.

As I noted earlier, usually the spectrum of the useful signal is in the lower part of the Nyquist band, and the spectrum of the noise is distributed throughout the Nyquist band, so we needed to find the cut-off frequency between the useful signal of the physicist and the flat white noise. How to find it? First, I learned from the physicist a theoretical model of the experiment that he had in his head - it was a lot of narrow spectral lines in the form of Gaussian functions on top of a wide Gaussian function (I doubted that this Cauchy distribution, but did not argue with it, because would be very small considering the nature of the data we had). So, we simulated this distribution, and he prepared a certain amount of synthetic data corresponding to this model. Fast spectral analysis of the signal through the fast Fourier transform, showed that the signal is enclosed in the lower 1/20 of the Nyquist band. Next, we processed its experimental data in the same way and obtained the same location of the cutoff frequency! What a luck! (Perhaps luck should be attributed to the skill of the experimenter). Once, theory and practice came together! It turned out that we were able to filter out 95% of the noise. Finally, Kaiser wrote for him a program that synthesized a filter for a given cut-off frequency, which the experimenter asked.

The program (1) calculated the appropriate differentiating filter, (2) wrote a program for calculating the smoothed output and after that (3) processed the data with this filter without any interference from the physicist.

Later, I caught a physicist adjusting the cut-off frequency for different parts of the energy level data obtained in one measurement series and was forced to remind him that there are certain “degrees of freedom” and what he does is not fair data processing. It became much more problematic when things were going well, to persuade him to get the most out of his data (the receipt of which was very expensive) - he had to work with the square roots of his impulses, since they had the same dispersion. Finally, he understood this and did so. He and Kaiser wrote a classic work in this area that opened the door to new things that could be done.

My contribution? Mostly, first identify the problem, then bring the right people together, then watch the Kaiser to put it in front of the fact that filtering is necessary not only for signals as a function of time, and finally remind them what they knew from the statistics (or should would know, but perhaps did not know).

On the basis of mine, it seems to me that the need for such a role increases as people become more and more profound experts in ever narrower fields of knowledge. Someone needs to maintain a broad outlook and ensure that things are done honestly. I think I came to this role after a very long education under the leadership of John Tukey in addition to a good foundation in the form of a universal tool of Science, called Mathematics. I will talk about maths nature inChapter 23 .

Most of the signal processing takes place over time. At the same time, most digital filters are designed for small, highly specialized studies, which are not necessarily associated with signals over time. Here I will ask you to be attentive in the future. Suppose you manage the business at the top, and you are interested in data that shows earlier labor costs in relation to equipment. It will be noisy data, but you still want to understand, in the usual sense, what is happening in the organization - what long-term processes occur - those that are so slow that people will comprehend them when they happen, but nevertheless understand and catching that is fundamentally important if you want to be a good manager. You will need a digital filter, to smooth the data and see hints on the trend, if it exists. You do not want to find a trend that does not exist, but if it exists, then you really want to know how it was before in order to predict what it is likely to be in the near future. In fact, you will want to see changes in the trend slope, if the data allows you to see it. Some signals, such as firepower relative to the ship’s displacement, are not time-bound, but they can tell you a lot about the current state of the fleet. Of course, you can study this relationship as a function of time. You will want to see changes in trend slope, if the data allows you to see it. Some signals, such as firepower relative to the ship’s displacement, are not time-bound, but they can tell you a lot about the current state of the fleet. Of course, you can study this relationship as a function of time. You will want to see changes in trend slope, if the data allows you to see it. Some signals, such as firepower relative to the ship’s displacement, are not time-bound, but they can tell you a lot about the current state of the fleet. Of course, you can study this relationship as a function of time.

At the top of your career, you will be able to use a variety of low-level digital filters for signals as a function of time and not just to better manage your business. Therefore, I argue that you are likely to synthesize much more digital filters for such non-standard things than to reduce the size of radar data and similar classic applications. Usually it is in new applications of knowledge that one can get the greatest return.

Let me express some concerns about the incorrect use of intelligent tools, in more detail I will talk about topics close to statistics in Chapter 27. Analysis by Fourier series expansion assumes linearity of the underlying model. You can use it for slightly non-linear cases, but more often, a cleverly done analysis by decomposition into Fourier series fails, because the phenomenon under study is too non-linear in nature. I saw millions of dollars being wasted, when it was rather obvious to outsiders, that non-linearities would distort all the linear analysis made by approximation by Fourier series. When they were pointed to this, their answer was that they did not know what other approach they could use, so they continued to do the wrong things! And I'm not exaggerating here.



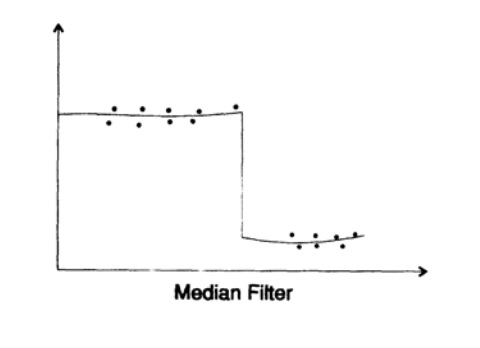
Figure 17.2

What about non-linear filters? The possibilities here are endless and depend, of course, on the problem you are dealing with. I will do here only one of them, the median filter. You consider the output of the median filter for a specific data set. Consider how it works in practice. First of all, we note that it seeks to smooth out any local noise, but how does the filter behave at the point of discontinuity (fig. 17.2)?

With an odd number of terms in the median filter, you will see that the filter output remains at the upper level until more than half of the filter input points are at the lower level, after which the filter output jumps down. It will follow the gaps well enough and will not try to smooth them completely! In some cases, this is exactly the type of filter that suits you - local noise is smoothed, and sudden changes in the state of the system being studied will not be lost.

I repeat that analysis using Fourier series is linear, at the same time there are a large number of non-linear filters, but the theory is not well developed for anything other than a median filter. The Kalman filter is another example of the use of a partially non-linear filter, the non-linear part is the self-tuning of the filter to the signal.

Finally, here is another fundamental observation that I made while studying digital filters. Once studying a book dedicated to Fourier integrals, I found a theorem that stated that the variation of a function multiplied by the variation of its transformation must be greater than a certain constant. I asked myself: “What is it like the famous uncertainty principle of Quantum Mechanics?” Yes, every linear theory should have an uncertainty principle relating the conjugate variables. As soon as you accept the linear approach, and the CM asserts the absolute additivity of the eigenstates, you should discover the uncertainty principle. The linear invariance of time automatically leads to eigenfunctions e ^ iω (t). They immediately lead to the Fourier series, and they in turn have the principle of uncertainty. It's as if you are wearing blue tinted glasses. Whatever you look at, it should have a bluish tint!

Therefore, you are not really sure whether the famous uncertainty principle of CM exists or not; it may just be the effect of the implied linearity of the system.

Few people want to believe that what we see depends on which side we come to the problem! Very often we see what we want to see, which is why you should apply the scientific approach everywhere, doubting your own convictions.
To demonstrate this clearly, I will repeat the story of Eddington about fishermen. They fished with a net, and when they examined the size of the net caught fish, they decided that there was a minimum size of fish in the sea.

In conclusion, if you do not doubt the accepted rules, now and then, then most likely you will not become leaders in any field, on the other hand, if you doubt everything, you will find yourself paralyzed and will not do anything . When to doubt, when to study the very basics, when to think independently, and when to just go ahead and accept things as they are - this is a matter of thinking style, and I cannot give a simple formula for solving this problem. You must learn from your experience. Big achievements usually come after significant changes in the basic assumptions on which the region is based. The state of our knowledge determines the balance between the various aspects of the study. It seems that when you are young, intuition and insight have more time to pay off, but when you are old,

To be continued ...

Who wants to help with the translation, layout and publication of the book - write in a personal or mail magisterludi2016@yandex.ru

By the way, we also started translating another cool book - “The Dream Machine: The History of Computer Revolution” )