Timsort Sort Algorithm
Timsort , unlike any “bubbles” and “inserts” there, is a relatively new thing - it was invented in 2002 by Tim Peters (named after him). Since then, it has already become the standard sorting algorithm in Python, OpenJDK 7, and Android JDK 1.5. And to understand why - just look at this plate from Wikipedia.
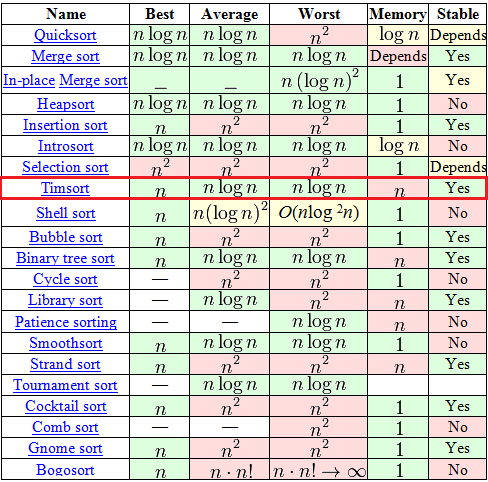
Among, at first glance, the huge selection in the table, there are only 7 adequate algorithms (with complexity O (n logn) in the average and worst case), among which only 2 can boast of stability and complexity O (n) in the best case. One of these two is the well-known “Sorting Using a Binary Tree” for a long time . But the second one is just the same Timsort.
The algorithm is based on the idea that in the real world, a sorted data array often contains ordered (it does not matter, ascending or descending) subarrays. This is indeed often the case. On such data, Timsort rips all other algorithms to shreds.
Do not expect any complicated mathematical discoveries here. The fact is that in fact Timsort is not a completely independent algorithm, but a hybrid, an effective combination of several other algorithms, seasoned with its own ideas. Very briefly, the essence of the algorithm can be explained as follows:

The number minrun is determined based on N based on the following principles:
So, at this stage, we have an input array, its size N and the calculated number minrun . The algorithm of this step:
At this stage, we have an input array, divided into subarrays, each of which is ordered. If the input array data was close to random - the size of the ordered subarrays is close to minrun , if the data had ordered ranges (and based on the recommendations on the application of the algorithm, we have reason to hope) - the ordered subarrays are larger than minrun .
Now we need to combine these subarrays to get the resulting, fully ordered array. Moreover, in the course of this association, 2 requirements must be fulfilled:
This is achieved in this way.
The purpose of this tricky procedure is to maintain balance. Those. the changes will look like this:

which means that the sizes of the subarrays in the stack are effective for further sorting by merge. Imagine an ideal case: we have subarrays of size 128, 64, 32, 16, 8, 4, 2, 2 (we forget for a second that there is a requirement “subarray size> = minrun ”). In this case, no mergers will be executed until the last 2 subarrays are met, but after that 7 perfectly balanced mergers will be performed.
As you remember, in the second step of the algorithm we are merging two subarrays into one ordered one. We always combine 2 consecutive subarrays. To merge them, additional memory is used.

Everything seems to be good in the merge algorithm shown above. Except one. Imagine a procedure for merging two such arrays like this:
A = {1, 2, 3, ..., 9999, 10000}
B = {20000, 20001, ...., 29999, 30000}
The above procedure will certainly work for them , but each time on its fourth paragraph you will need to perform one comparison and one copy. And that 10,000 comparisons and 10,000 copies. The Timsort algorithm offers in this place a modification that he calls a gallop. The bottom line is:
Perhaps the explanation is a bit vague, let's try an example.
A = {1, 2, 3, ..., 9999, 10000}
B = {20000, 20001, ...., 29999, 30000}
That's the whole algorithm.

Among, at first glance, the huge selection in the table, there are only 7 adequate algorithms (with complexity O (n logn) in the average and worst case), among which only 2 can boast of stability and complexity O (n) in the best case. One of these two is the well-known “Sorting Using a Binary Tree” for a long time . But the second one is just the same Timsort.
The algorithm is based on the idea that in the real world, a sorted data array often contains ordered (it does not matter, ascending or descending) subarrays. This is indeed often the case. On such data, Timsort rips all other algorithms to shreds.
Straight to the point
Do not expect any complicated mathematical discoveries here. The fact is that in fact Timsort is not a completely independent algorithm, but a hybrid, an effective combination of several other algorithms, seasoned with its own ideas. Very briefly, the essence of the algorithm can be explained as follows:
- By a special algorithm, we divide the input array into subarrays.
- We sort each subarray by the usual sorting by inserts .
- We collect the sorted subarrays into a single array using the modified merge sort .
Algorithm
Concepts used
- N - input array size
- run is an ordered subarray in the input array. Moreover, ordered or non-strictly ascending, or strictly descending. That is, either "a0 <= a1 <= a2 <= ...", or "a0> a1> a2> ..."
- minrun - as mentioned above, at the first step of the algorithm, the input array will be divided into subarrays. minrun is the minimum size of such a subarray. This number is calculated according to a certain logic of number of N .

Step 0. Calculation of minrun .
The number minrun is determined based on N based on the following principles:
- It should not be too large, since insertion sorting will be applied to the minrun size subarray in the future, and it is effective only on small arrays
- It should not be too small, because the smaller the subarray, the more iterations of merging the subarrays will have to be performed at the last step of the algorithm.
- It would be nice if N \ minrun was a power of 2 (or close to it). This requirement is due to the fact that the algorithm for merging subarrays most effectively works on subarrays of approximately equal size.
int GetMinrun(int n)
{
int r = 0; /* станет 1 если среди сдвинутых битов будет хотя бы 1 ненулевой */
while (n >= 64) {
r |= n & 1;
n >>= 1;
}
return n + r;
}Step 1. Splitting into subarrays and sorting them.
So, at this stage, we have an input array, its size N and the calculated number minrun . The algorithm of this step:
- We put the pointer of the current element at the beginning of the input array.
- Starting from the current element, we look in the input array for run (an ordered subarray). By definition, this run will unambiguously include the current element and the next one, but further on, it’s already lucky. If the resulting subarray is ordered in descending order, we rearrange the elements so that they go in ascending order (this is a simple linear algorithm, just go from both ends to the middle, swapping the elements).
- If the size of the current run 'is less than minrun - we take the following elements after the found run th in the amount of minrun - size (run) . Thus, at the output we get a subarray of size minrun or larger, part of which (and ideally all of it) is ordered.
- We apply insertion sorting to this subarray. Since the size of the subarray is small and part of it is already ordered - sorting works quickly and efficiently.
- We put the pointer to the current element next to the subarray element.
- If the end of the input array is not reached - go to step 2, otherwise - the end of this step.
Step 2. Merge.
At this stage, we have an input array, divided into subarrays, each of which is ordered. If the input array data was close to random - the size of the ordered subarrays is close to minrun , if the data had ordered ranges (and based on the recommendations on the application of the algorithm, we have reason to hope) - the ordered subarrays are larger than minrun .
Now we need to combine these subarrays to get the resulting, fully ordered array. Moreover, in the course of this association, 2 requirements must be fulfilled:
- Combine subarrays of approximately equal size (this is more efficient).
- Keep the algorithm stable - i.e. Do not make meaningless permutations (for example, do not swap two consecutive identical numbers in places).
This is achieved in this way.
- Create an empty stack of pairs <index of the beginning of the subarray> - <size of the subarray>. Take the first ordered subarray.
- Add to the stack a pair of data <start index> - <size> for the current subarray.
- Determine whether to merge the current subarray with the previous ones. To do this, check the implementation of 2 rules (let X, Y and Z be the sizes of the top three in the stack of subarrays):
X> Y + Z
Y> Z - If one of the rules is violated, the array Y merges with the smaller of the arrays X and Z. It is repeated until both rules are fulfilled or the data is completely ordered.
- If there are still not considered subarrays, we take the next one and go to step 2. Otherwise, the end.
The purpose of this tricky procedure is to maintain balance. Those. the changes will look like this:

which means that the sizes of the subarrays in the stack are effective for further sorting by merge. Imagine an ideal case: we have subarrays of size 128, 64, 32, 16, 8, 4, 2, 2 (we forget for a second that there is a requirement “subarray size> = minrun ”). In this case, no mergers will be executed until the last 2 subarrays are met, but after that 7 perfectly balanced mergers will be performed.
Subarray Merge Procedure
As you remember, in the second step of the algorithm we are merging two subarrays into one ordered one. We always combine 2 consecutive subarrays. To merge them, additional memory is used.
- We create a temporary array in the size of the smallest of the connected subarrays.
- Copy the smaller of the subarrays to a temporary array
- We put the current position pointers on the first elements of a larger and temporary array.
- At each next step, we consider the value of the current elements in the larger and temporary arrays, take the smaller of them and copy it into a new sorted array. We move the pointer of the current element in the array from which the element was taken.
- Repeat 4 until one of the arrays ends.
- Add all the elements of the remaining array to the end of the new array.

Modification of the procedure for merging subarrays
Everything seems to be good in the merge algorithm shown above. Except one. Imagine a procedure for merging two such arrays like this:
A = {1, 2, 3, ..., 9999, 10000}
B = {20000, 20001, ...., 29999, 30000}
The above procedure will certainly work for them , but each time on its fourth paragraph you will need to perform one comparison and one copy. And that 10,000 comparisons and 10,000 copies. The Timsort algorithm offers in this place a modification that he calls a gallop. The bottom line is:
- We begin the merge procedure, as shown above.
- At each operation of copying an element from a temporary or larger subarray to the resulting one, we remember from which subarray the element was.
- If already a certain number of elements (in this implementation of the algorithm this number is rigidly equal to 7) was taken from the same array - we assume that we will have to take data from it further. To confirm this idea, we switch to gallop mode, i.e. we’ll run through the candidate array for the supply of the next large portion of data by binary search (we remember that the array is ordered and we have every right to binary search) of the current element from the second array to be connected. Binary search is more effective than linear, and therefore search operations will be much less.
- Having finally found the moment when the data from the current provider array no longer suits us (or reaching the end of the array), we can finally copy them all at once (which can be more efficient than copying single elements).
Perhaps the explanation is a bit vague, let's try an example.
A = {1, 2, 3, ..., 9999, 10000}
B = {20000, 20001, ...., 29999, 30000}
- The first 7 iterations, we compare the numbers 1, 2, 3, 4, 5, 6, and 7 from array A with the number 20,000, and making sure that 20,000 more, copy the elements of array A to the resulting one.
- Starting from the next iteration, we switch to the “gallop” mode: compare the elements 8, 10, 14, 22, 38, n + 2 ^ i, ..., 10000 of array A with the number 20,000 in succession . As you can see, such a comparison will be much less than 10,000.
- We have reached the end of array A and we know that it is all smaller than B (we could also stop somewhere in the middle). Copy the necessary data from array A to the resulting one, and move on.
That's the whole algorithm.
