The probability of winning the match with a known probability of winning points II
If you have not read my first article on the topic, I advise you to start with it .
Since I have spoken about some, although very indirectly related to financial mathematicians, let me develop the topic to the point of absurdity based on how it is developed in Risk Analytics. When calculating the price of an option, the sensitivity of this price to a set of parameters is often also considered. For example, how will the price of an option change when the price of a stock for which the option is issued changes, or when the price of a share changes, or if the Central Bank rates, etc.
We may be interested in how the probability of winning a game changes when the probability of a point is changed. In fact, we want to calculate the derivative from the first to the second. The simplest approach is to evaluate it by eye from the graph. It can be seen that the maximum is reached in a 50:50 situation. If you change the chance of winning points from 0.45 to 0.55, the probability of winning badminton increases from 0.26 to 0.74, that is, by 0.48. A rough estimate gives a derivative in the region of 5. That is, if with equal chances you grow to 0.51 (that is 51%), the increase in the probability of winning the game will be about 0.05 (or 5%). Similarly, you can calculate the derivative at any other point on the graph.
In finance, the “bump and run” approach is usually used, that is, they change the parameter by a small amount and calculate the new option price and derivative. Doing the same thing, I bring exact data on the graph (I took the change by a percentage, a little rough, but acceptable in this situation). For greater clarity, added the game to 5 and 31 points. By the way, shooting in biathlon can be considered as a batch of up to 5. This is not an absolute analogy, since the total number of shots is fixed. But the solutions are almost the same.
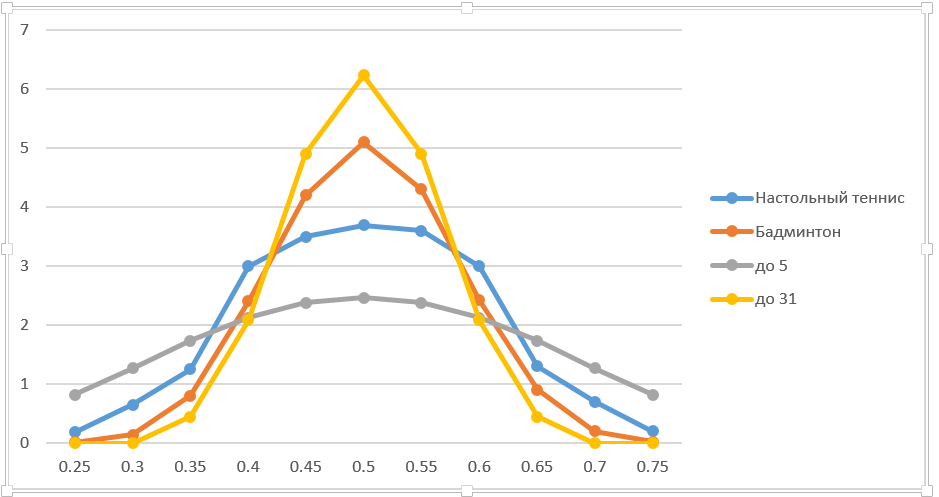
Obviously, the longer the batch, the higher the derivative at 50:50. When the length of a game tends to infinity, the victory of a player who has even a minimal advantage is practically guaranteed. The width of the curve decreases accordingly. In general, the conclusions are quite obvious.
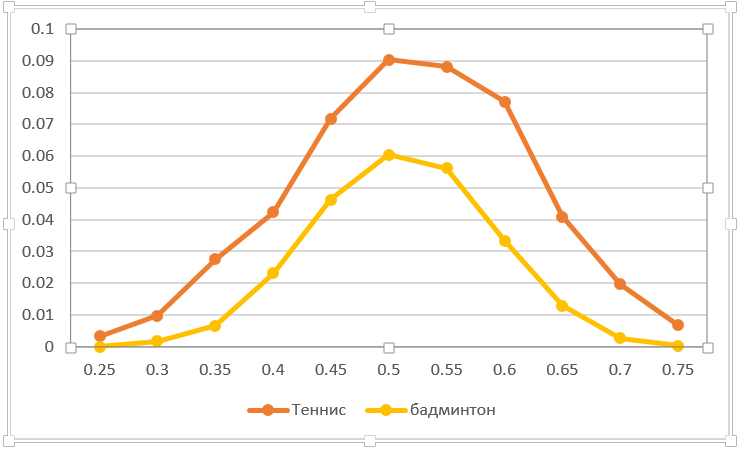
You can calculate the sensitivity to a random discharge of one point. For example, feed to the grid. How much does one slip affect the outcome of the game? In fact, this is a reduction in the winning score for an opponent by one point. The chart below reflects this situation. Naturally, in table tennis it is more critical to lose a point than in badminton. With equal forces, the probability of the outcome of the game falls as much as possible - from 0.5 to 0.41. Note the asymmetry of the curves (unlike most others). This is not an accident. The fact is that the equilibrium shifts from 50:50 towards a higher probability of scoring, since a lost point worsens a player's chances.
Let's put another curious experience. Imagine that one of the players can concentrate and play 3 points above the average (p1 + delta). Suppose that after this alignment will return to the original (to the average expected without taking into account the "surge of strength"). It is clear that the probability of winning will increase. The question is, does it matter exactly when to concentrate - at the beginning or at the end of the game? I suggest to make a guess before reading further.
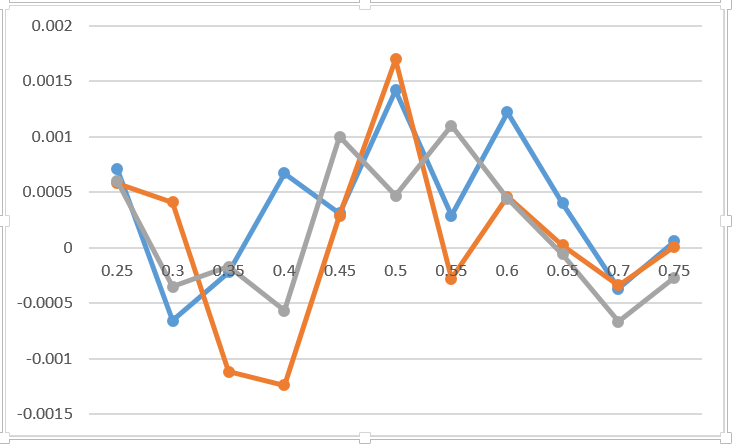
So, as the experiment shows, there is absolutely no difference when it is to concentrate (moral factors are not taken into account). The graph shows the difference between the probability of winning the game in the case of concentration in 3 different places of the party compared to the concentration on the first 3 points. I think this chart reflects the error of Monte Carlo and nothing more. I added 0.2 to the outcome of scoring for the first player for three draws. I do not even indicate on the graph which line corresponds to which variant. It definitely does not change anything. The only valuable advice on this topic - get together before it is too late.
Now let's discuss what will happen if one of the players has stability. Nerves are nerves, a responsible game, it happens. Suppose, on average, he is gaining the same percentage of points, but when a particular point is drawn, this percentage floats. For example, half the points are played with the probability p1 + delta, and the other half with p1-delta. In this case, the average p1 remains the initial one, and + delta or –delta drops out at random with a probability of 0.5. Will it somehow affect the outcome of the game? As shown by my experiments with the help of Monte Carlo, the difference is hardly visible. In fact, by adding or subtracting a certain amount, albeit randomly, we remain at the same average probability of scoring. This suggests that the distribution curve does not affect the outcome of the game, but only the average, but I will not take it upon myself. Here we must think.
I would also like to derive a differential equation, such as Black Scholes in finance, to complete the associations. Identify significant derivatives, zero the random component ... More and with the discreteness must be dealt with. I guess I'll leave it to real financial mathematicians.
Since I have spoken about some, although very indirectly related to financial mathematicians, let me develop the topic to the point of absurdity based on how it is developed in Risk Analytics. When calculating the price of an option, the sensitivity of this price to a set of parameters is often also considered. For example, how will the price of an option change when the price of a stock for which the option is issued changes, or when the price of a share changes, or if the Central Bank rates, etc.
We may be interested in how the probability of winning a game changes when the probability of a point is changed. In fact, we want to calculate the derivative from the first to the second. The simplest approach is to evaluate it by eye from the graph. It can be seen that the maximum is reached in a 50:50 situation. If you change the chance of winning points from 0.45 to 0.55, the probability of winning badminton increases from 0.26 to 0.74, that is, by 0.48. A rough estimate gives a derivative in the region of 5. That is, if with equal chances you grow to 0.51 (that is 51%), the increase in the probability of winning the game will be about 0.05 (or 5%). Similarly, you can calculate the derivative at any other point on the graph.
In finance, the “bump and run” approach is usually used, that is, they change the parameter by a small amount and calculate the new option price and derivative. Doing the same thing, I bring exact data on the graph (I took the change by a percentage, a little rough, but acceptable in this situation). For greater clarity, added the game to 5 and 31 points. By the way, shooting in biathlon can be considered as a batch of up to 5. This is not an absolute analogy, since the total number of shots is fixed. But the solutions are almost the same.

Obviously, the longer the batch, the higher the derivative at 50:50. When the length of a game tends to infinity, the victory of a player who has even a minimal advantage is practically guaranteed. The width of the curve decreases accordingly. In general, the conclusions are quite obvious.
You can calculate the sensitivity to a random discharge of one point. For example, feed to the grid. How much does one slip affect the outcome of the game? In fact, this is a reduction in the winning score for an opponent by one point. The chart below reflects this situation. Naturally, in table tennis it is more critical to lose a point than in badminton. With equal forces, the probability of the outcome of the game falls as much as possible - from 0.5 to 0.41. Note the asymmetry of the curves (unlike most others). This is not an accident. The fact is that the equilibrium shifts from 50:50 towards a higher probability of scoring, since a lost point worsens a player's chances.

Let's put another curious experience. Imagine that one of the players can concentrate and play 3 points above the average (p1 + delta). Suppose that after this alignment will return to the original (to the average expected without taking into account the "surge of strength"). It is clear that the probability of winning will increase. The question is, does it matter exactly when to concentrate - at the beginning or at the end of the game? I suggest to make a guess before reading further.

So, as the experiment shows, there is absolutely no difference when it is to concentrate (moral factors are not taken into account). The graph shows the difference between the probability of winning the game in the case of concentration in 3 different places of the party compared to the concentration on the first 3 points. I think this chart reflects the error of Monte Carlo and nothing more. I added 0.2 to the outcome of scoring for the first player for three draws. I do not even indicate on the graph which line corresponds to which variant. It definitely does not change anything. The only valuable advice on this topic - get together before it is too late.
Now let's discuss what will happen if one of the players has stability. Nerves are nerves, a responsible game, it happens. Suppose, on average, he is gaining the same percentage of points, but when a particular point is drawn, this percentage floats. For example, half the points are played with the probability p1 + delta, and the other half with p1-delta. In this case, the average p1 remains the initial one, and + delta or –delta drops out at random with a probability of 0.5. Will it somehow affect the outcome of the game? As shown by my experiments with the help of Monte Carlo, the difference is hardly visible. In fact, by adding or subtracting a certain amount, albeit randomly, we remain at the same average probability of scoring. This suggests that the distribution curve does not affect the outcome of the game, but only the average, but I will not take it upon myself. Here we must think.
I would also like to derive a differential equation, such as Black Scholes in finance, to complete the associations. Identify significant derivatives, zero the random component ... More and with the discreteness must be dealt with. I guess I'll leave it to real financial mathematicians.
