Fundamentals of number systems
Studying encodings, I realized that I do not understand well the number systems. Nevertheless, he often used the 2-, 8-, 10-, 16th systems, transferred one to another, but everything was done on the “machine”. After reading many publications, I was surprised at the lack of a single, simple language article on such basic material. That is why I decided to write my own, in which I tried to explain the fundamentals of number systems in an accessible and orderly way.
The number system is a way of recording (presenting) numbers.
What is meant by this? For example, you see several trees in front of you. Your task is to count them. To do this, you can - bend your fingers, make nicks on a stone (one tree - one finger / notch), or assign 10 objects to some trees, for example, a stone, and to a single copy - a stick and lay them on the ground as they are counted. In the first case, the number is represented as a string of bent fingers or nicks, in the second - a composition of stones and sticks, where the stones are on the left and the sticks are on the right.
The number systems are divided into positional and non-positional, and positional, in turn, into homogeneous and mixed.
Non-positional- the oldest, in it each digit of the number has a value that does not depend on its position (discharge). That is, if you have 5 dashes, then the number is also 5, since each dash, regardless of its place in the line, corresponds to only 1 single item.
Positional system - the value of each digit depends on its position (rank) in the number. For example, the 10th number system familiar to us is positional. Consider the number 453. The number 4 denotes the number of hundreds and corresponds to the number 400, 5 - the number of tens and is similar to the value 50, and 3 - units and the value 3. As you can see - the larger the discharge - the higher the value. The final number can be represented as the sum of 400 + 50 + 3 = 453.
Homogeneous system- for all digits (positions) of the number, the set of valid characters (digits) is the same. As an example, take the 10th system mentioned earlier. When writing a number in a homogeneous 10th system, you can use only one digit from 0 to 9 in each digit, so the number 450 is allowed (1st digit - 0, 2nd digit - 5, 3rd digit - 4), and 4F5 - no, because the F symbol is not included in the set of digits from 0 to 9.
Mixed system - in each digit (position) of the number, the set of valid characters (digits) may differ from the sets of other digits. A vivid example is a time measurement system. In the category of seconds and minutes, 60 different characters are possible (from "00" to "59"), in the category of hours - 24 different characters (from "00" to "23"), in the category of day - 365, etc.
As soon as people learned to count, there was a need to write numbers. In the beginning, everything was simple - a notch or a dash on any surface corresponded to one object, for example, one fruit. So the first number system appeared - single.
The number in this number system is a string of dashes (sticks), the number of which is equal to the value of this number. Thus, a crop of 100 dates will be equal to the number consisting of 100 dashes.
But this system has obvious inconveniences - the larger the number - the longer the string of sticks. In addition, you can easily make a mistake when writing a number by accidentally adding an extra stick or, conversely, not adding.
For convenience, people began to group sticks in 3, 5, 10 pieces. At the same time, each group corresponded to a certain sign or object. Initially, fingers were used for counting, so the first signs appeared for groups of 5 and 10 pieces (units). All this made it possible to create more convenient number recording systems.
In ancient Egypt, special characters (numbers) were used to designate the numbers 1, 10, 10 2 , 10 3 , 10 4 , 10 5 , 10 6 , 10 7 . Here are some of them:
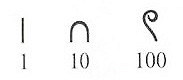
Why is it called decimal? As stated above - people began to group symbols. In Egypt, they chose a group of 10, leaving the number “1” unchanged. In this case, the number 10 is called the base of the decimal number system, and each character is a representation of the number 10 to some extent.
Numbers in the ancient Egyptian number system were written as a combination of these
characters, each of which was repeated no more than nine times. The total value was equal to the sum of the elements of the number. It is worth noting that this method of obtaining values is characteristic of each non-positional number system. An example is the number 345:

In contrast to the Egyptian, in the Babylonian system, only 2 symbols were used: a “direct” wedge to indicate units and a “lying” one for dozens. To determine the value of a number, it is necessary to break the image of the number into digits from right to left. A new discharge begins with the appearance of a direct wedge after a recumbent one. As an example, let's take the number 32:

The number 60 and all its degrees are also denoted by a straight wedge as “1”. Therefore, the Babylonian number system was called six-decimal.
All numbers from 1 to 59 were written by the Babylonians in the decimal non-positional system, and large values in the positional with a base of 60. Number 92:

The record of the number was ambiguous, since there was no digit denoting zero. The representation of the number 92 could mean not only 92 = 60 + 32, but also, for example, 3632 = 3600 + 32. To determine the absolute value of the number, a special character was introduced to indicate the missing six-digit digit, which corresponds to the appearance of the digit 0 in the decimal number record:
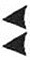
Now the number 3632 should be written as: The six-decimal

Babylonian system is the first number system, partially based on the positional principle. This number system is used today, for example, when determining the time - an hour consists of 60 minutes, and a minute of 60 seconds.
The Roman system is not very different from the Egyptian. In it, to indicate the numbers 1, 5, 10, 50, 100, 500 and 1000, the capital letters of the Latin alphabet are I, V, X, L, C, D and M, respectively. A number in the Roman numeral system is a set of consecutive digits.
Methods for determining the value of a number:
In addition to digital, there are also alphabetic (numeric) number systems, here are some of them:
1) Slavic
2) Greek (Ionian)
As mentioned above, the first prerequisites for the emergence of a positional system arose in ancient Babylon. In India, the system took the form of positional decimal numbering using zero, and the Indians borrowed this system of numbers from the Arabs, from whom the Europeans adopted it. For some reason, in Europe, the name “Arab” was assigned to this system.
This is one of the most common number systems. We use it when we call the price of the goods and pronounce the number of the bus. In each category (position), only one digit can be used from the range from 0 to 9. The base of the system is the number 10.
For example, take the number 503. If this number were recorded in a non-positional system, then its value would be 5 + 0 + 3 = 8. But we have a positional system and it means that each digit of the number must be multiplied by the base of the system, in this case the number “10”, raised to a power equal to the number of the category. It turns out that the value is 5 * 10 2 + 0 * 10 1 + 3 * 10 0= 500 + 0 + 3 = 503. In order to avoid confusion while simultaneously working with several number systems, the base is indicated as a subscript. Thus, 503 = 503 10 .
In addition to the decimal system, the 2nd, 8th, and 16th systems deserve special attention.
This system is mainly used in computer technology. Why didn’t you use the 10th familiar to us? The first computing machine was created by Blaise Pascal, who used a decimal system in it, which turned out to be inconvenient in modern electronic machines, because it required the production of devices capable of operating in 10 states, which increased their price and the total size of the machine. These drawbacks are deprived of elements operating in the 2nd system. Nevertheless, the system in question was created long before the invention of computers and goes back to the Inca civilization, where a pile of complex rope plexuses and knots were used.
The binary positional number system has a base of 2 and uses 2 characters (digits) to write the number 2: 0 and 1. In each digit, only one digit is allowed - either 0 or 1. The
number 101 can be an example. It is similar to the number 5 in the decimal number system . In order to transfer from the 2nd to the 10th it is necessary to multiply each digit of the binary number by the base “2”, raised to a power equal to the category. Thus, the number 101 2 = 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5 10 .
Well, for machines the 2nd number system is more convenient, but we often see, we use numbers in the 10th system on the computer. How then does the machine determine which digit the user enters? How does a number translate from one system to another, because it has only 2 characters at its disposal - 0 and 1?
In order for a computer to work with binary numbers (codes), they must be stored somewhere. To store each individual digit, a trigger is used, which is an electronic circuit. It can be in 2 states, one of which corresponds to zero, the other to unity. To remember a single number, a register is used - a group of triggers, the number of which corresponds to the number of bits in a binary number. And the set of registers is RAM. The number contained in the register is a machine word. Arithmetic and logical operations with words are carried out by an arithmetic-logical device (ALU). To simplify access to the registers, they are numbered. The number is called the register address. For example, if you need to add 2 numbers, it is enough to indicate the numbers of cells (registers) in which they are located, and not the numbers themselves. Addresses are written in 8- and hexadecimal systems (they will be described below), since the transition from them to the binary system and vice versa is quite simple. To transfer from the 2nd to the 8th, it is necessary to divide into groups of 3 digits from right to left, and to go to the 16th, to 4. If the digits do not reach the digits in the leftmost group, they are filled with zeros on the left, which are called zeros leading. As an example, take the number 1011002 . In octal it is 101 100 = 54 8 , and in hexadecimal it is 0010 1100 = 2С 16 . Great, but why do we see decimal numbers and letters on the screen? When a key is pressed, a certain sequence of electrical pulses is transmitted to the computer, with each symbol having its own sequence of electrical pulses (zeros and ones). The keyboard and screen driver program accesses the character code table (for example, Unicode, which allows you to encode 65536 characters), determines which character the received code corresponds to and displays it on the screen. Thus, the texts and numbers are stored in binary memory in the computer's memory, and programmatically converted to images on the screen.
The 8th number system, like binary, is often used in digital technology. It has a base of 8 and uses digits from 0 to 7 to record the number.
An example of an octal number: 254. To transfer to the 10th system, each digit of the original number must be multiplied by 8 n , where n is the number of the digit. It turns out that 254 8 = 2 * 8 2 + 5 * 8 1 + 4 * 8 0 = 128 + 40 + 4 = 172 10 .
The hexadecimal system is widely used in modern computers, for example, using it, the color is indicated: #FFFFFF - white color. The system in question has a base of 16 and uses to write the numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, where the letters are 10, 11, 12, 13, 14, 15, respectively.
Take 4F5 16 as an example . To translate into the octal system, first convert the hexadecimal number to binary, and then, breaking into groups of 3 digits, into octal. To convert a number to 2nd, each digit must be represented as a 4-bit binary number. 4F5 16 = (100 1111 101) 2. But there is no discharge in groups 1 and 3, so fill each with leading zeros: 0100 1111 0101. Now you need to divide the resulting number into groups of 3 digits from right to left: 0100 1111 0101 = 010 011 110 101. We translate each binary group into an octal system, multiplying each bit by 2 n , where n is the bit number: (0 * 2 2 + 1 * 2 1 + 0 * 2 0 ) (0 * 2 2 + 1 * 2 1 + 1 * 2 0 ) (1 * 2 2 + 1 * 2 1 + 0 * 2 0 ) (1 * 2 2 + 0 * 2 1 + 1 * 2 0 ) = 2365 8 .
In addition to the considered positional number systems, there are others, for example:
1) Trinitarian
2) Quaternary
3) Duodecimal
Positional systems are divided into homogeneous and mixed.
The definition given at the beginning of the article adequately describes homogeneous systems, so the refinement is unnecessary.
We can add the theorem to the above definition: “if P = Q n (P, Q, n are positive integers, and P and Q are bases), then the notation of any number in the mixed (PQ) number system identically coincides with by writing the same number in the number system with the base Q. ”
Based on the theorem, we can formulate the rules for the transfer from the Pth to the Qth system and vice versa:
A striking example is the conversion from binary to octal. Let's take the binary number 10011110 2 , to convert it to octal, we divide it from right to left into groups of 3 digits: 010 011 110, now multiply each digit by 2 n , where n is the digit number, 010 011 110 = (0 * 2 2 +1 * 2 1 + 0 * 2 0 ) (0 * 2 2 + 1 * 2 1 + 1 * 2 0 ) (1 * 2 2 + 1 * 2 1 + 0 * 2 0 ) = 236 8 . It turns out that 10011110 2 = 236 8 . For the uniqueness of the image of the binary octal number, it is divided into triples: 236 8= (10 011 110) 2-8 .
Mixed number systems are also, for example:
1) Factorial
2) Fibonacci
Sometimes it is necessary to convert a number from one number system to another, therefore, we consider the methods of translation between different systems.
There is a number a 1 a 2 a 3 in the number system with base b. To transfer to the 10th system, it is necessary to multiply each bit of the number by b n , where n is the number of the bit. Thus, (a 1 a 2 a 3 ) b = (a 1 * b 2 + a 2 * b 1 + a 3 * b 0 ) 10 .
Example: 101 2 = 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5 10
The whole part:
Fractional part:
Example: translate 15 10 to octal:
15 \ 8 = 1, remainder 7
1 \ 8 = 0, remainder 1
Having written down all the rests from bottom to top, we get the final number 17. Therefore, 15 10 = 17 8 .
To convert to octal, we divide the binary number into groups of 3 digits from right to left, and fill in the missing extreme digits with leading zeros. Next, we transform each group by sequentially multiplying the digits by 2 n , where n is the number of the digit.
As an example, take the number 1001 2 : 1001 2 = 001 001 = (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ) (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ) = (0+ 0 + 1) (0 + 0 + 1) = 11 8
For translation into hexadecimal, we divide the binary number into groups of 4 digits from right to left, then - similarly, from the 2nd to the 8th.
Translation from octal to binary - we convert each digit of the octal number to binary 3-digit number by dividing by 2 (for more details on dividing, see the section “Converting from decimal number system to others” above), fill in the missing extreme digits with leading zeros.
For example, consider the number 45 8 : 45 = (100) (101) = 100101 2
Transfer from the 16th to the 2nd - we convert each digit of the hexadecimal number into a binary 4-digit number by dividing by 2, fill in the missing extreme digits with leading zeros .
Conversion of the fractional part of any number system to decimal
Conversion is carried out as for the whole parts, except that the digits of the number are multiplied by the base to the power of “-n”, where n starts from 1.
Example: 101.011 2 = (1 * 2 2 + 0 * 2 1 + 1 * 2 0 ), (0 * 2 -1 + 1 * 2 -2 + 1 * 2 -3 ) = (5), (0 + 0 , 25 + 0.125) = 5.375 10
The fractional part is translated in the same way as for the integer parts of the number, with the exception of the fact that the breakdown into groups of 3 and 4 digits goes to the right of the decimal point, the missing digits are supplemented with zeros on the right.
Example: 1001.01 2 = 001 001, 010 = (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ) (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ), (0 * 2 2 + 1 * 2 1 + 0 * 2 0 ) = (0 + 0 + 1) (0 + 0 + 1), (0 + 2 + 0) = 11.2 8
To translate the fractional part of a number into other number systems, you need to turn the integer part to zero and start multiplying the resulting number by the base of the system into which you want to translate. If as a result of multiplication the integer parts appear again, they must be turned back to zero, having previously memorized (written down) the value of the resulting integer part. The operation ends when the fractional part is completely zero.
For example, we translate 10.625 10 into the binary system:
0.625 * 2 = 1.25
0.250 * 2 = 0.5
0.5 * 2 = 1.0
Having written down all the residuals from top to bottom, we get 10.625 10 = (1010), (101) = 1010,101 2
Introduction
The number system is a way of recording (presenting) numbers.
What is meant by this? For example, you see several trees in front of you. Your task is to count them. To do this, you can - bend your fingers, make nicks on a stone (one tree - one finger / notch), or assign 10 objects to some trees, for example, a stone, and to a single copy - a stick and lay them on the ground as they are counted. In the first case, the number is represented as a string of bent fingers or nicks, in the second - a composition of stones and sticks, where the stones are on the left and the sticks are on the right.
The number systems are divided into positional and non-positional, and positional, in turn, into homogeneous and mixed.
Non-positional- the oldest, in it each digit of the number has a value that does not depend on its position (discharge). That is, if you have 5 dashes, then the number is also 5, since each dash, regardless of its place in the line, corresponds to only 1 single item.
Positional system - the value of each digit depends on its position (rank) in the number. For example, the 10th number system familiar to us is positional. Consider the number 453. The number 4 denotes the number of hundreds and corresponds to the number 400, 5 - the number of tens and is similar to the value 50, and 3 - units and the value 3. As you can see - the larger the discharge - the higher the value. The final number can be represented as the sum of 400 + 50 + 3 = 453.
Homogeneous system- for all digits (positions) of the number, the set of valid characters (digits) is the same. As an example, take the 10th system mentioned earlier. When writing a number in a homogeneous 10th system, you can use only one digit from 0 to 9 in each digit, so the number 450 is allowed (1st digit - 0, 2nd digit - 5, 3rd digit - 4), and 4F5 - no, because the F symbol is not included in the set of digits from 0 to 9.
Mixed system - in each digit (position) of the number, the set of valid characters (digits) may differ from the sets of other digits. A vivid example is a time measurement system. In the category of seconds and minutes, 60 different characters are possible (from "00" to "59"), in the category of hours - 24 different characters (from "00" to "23"), in the category of day - 365, etc.
Non Positioning Systems
As soon as people learned to count, there was a need to write numbers. In the beginning, everything was simple - a notch or a dash on any surface corresponded to one object, for example, one fruit. So the first number system appeared - single.
Single number system
The number in this number system is a string of dashes (sticks), the number of which is equal to the value of this number. Thus, a crop of 100 dates will be equal to the number consisting of 100 dashes.
But this system has obvious inconveniences - the larger the number - the longer the string of sticks. In addition, you can easily make a mistake when writing a number by accidentally adding an extra stick or, conversely, not adding.
For convenience, people began to group sticks in 3, 5, 10 pieces. At the same time, each group corresponded to a certain sign or object. Initially, fingers were used for counting, so the first signs appeared for groups of 5 and 10 pieces (units). All this made it possible to create more convenient number recording systems.
Ancient Egyptian Decimal System
In ancient Egypt, special characters (numbers) were used to designate the numbers 1, 10, 10 2 , 10 3 , 10 4 , 10 5 , 10 6 , 10 7 . Here are some of them:
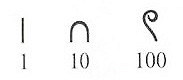
Why is it called decimal? As stated above - people began to group symbols. In Egypt, they chose a group of 10, leaving the number “1” unchanged. In this case, the number 10 is called the base of the decimal number system, and each character is a representation of the number 10 to some extent.
Numbers in the ancient Egyptian number system were written as a combination of these
characters, each of which was repeated no more than nine times. The total value was equal to the sum of the elements of the number. It is worth noting that this method of obtaining values is characteristic of each non-positional number system. An example is the number 345:

Babylonian Six Decimal System
In contrast to the Egyptian, in the Babylonian system, only 2 symbols were used: a “direct” wedge to indicate units and a “lying” one for dozens. To determine the value of a number, it is necessary to break the image of the number into digits from right to left. A new discharge begins with the appearance of a direct wedge after a recumbent one. As an example, let's take the number 32:

The number 60 and all its degrees are also denoted by a straight wedge as “1”. Therefore, the Babylonian number system was called six-decimal.
All numbers from 1 to 59 were written by the Babylonians in the decimal non-positional system, and large values in the positional with a base of 60. Number 92:

The record of the number was ambiguous, since there was no digit denoting zero. The representation of the number 92 could mean not only 92 = 60 + 32, but also, for example, 3632 = 3600 + 32. To determine the absolute value of the number, a special character was introduced to indicate the missing six-digit digit, which corresponds to the appearance of the digit 0 in the decimal number record:
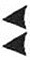
Now the number 3632 should be written as: The six-decimal

Babylonian system is the first number system, partially based on the positional principle. This number system is used today, for example, when determining the time - an hour consists of 60 minutes, and a minute of 60 seconds.
Roman system
The Roman system is not very different from the Egyptian. In it, to indicate the numbers 1, 5, 10, 50, 100, 500 and 1000, the capital letters of the Latin alphabet are I, V, X, L, C, D and M, respectively. A number in the Roman numeral system is a set of consecutive digits.
Methods for determining the value of a number:
- The value of a number is equal to the sum of the values of its digits. For example, the number 32 in the Roman numeral system has the form XXXII = (X + X + X) + (I + I) = 30 + 2 = 32
- If the smaller digit is to the left of the larger digit, then the value is equal to the difference between the larger and smaller digits. Moreover, the left digit can be less than the right one by a maximum of one order of magnitude: so, in front of L (50) and C (100) of the “younger” only X (10) can stand, in front of D (500) and M (1000) - only C (100), before V (5) - only I (1); the number 444 in the considered number system will be written in the form CDXLIV = (DC) + (LX) + (VI) = 400 + 40 + 4 = 444.
- The value is equal to the sum of the values of groups and numbers that do not fit under 1 and 2 points.
In addition to digital, there are also alphabetic (numeric) number systems, here are some of them:
1) Slavic
2) Greek (Ionian)
Positional number systems
As mentioned above, the first prerequisites for the emergence of a positional system arose in ancient Babylon. In India, the system took the form of positional decimal numbering using zero, and the Indians borrowed this system of numbers from the Arabs, from whom the Europeans adopted it. For some reason, in Europe, the name “Arab” was assigned to this system.
Decimal number system
This is one of the most common number systems. We use it when we call the price of the goods and pronounce the number of the bus. In each category (position), only one digit can be used from the range from 0 to 9. The base of the system is the number 10.
For example, take the number 503. If this number were recorded in a non-positional system, then its value would be 5 + 0 + 3 = 8. But we have a positional system and it means that each digit of the number must be multiplied by the base of the system, in this case the number “10”, raised to a power equal to the number of the category. It turns out that the value is 5 * 10 2 + 0 * 10 1 + 3 * 10 0= 500 + 0 + 3 = 503. In order to avoid confusion while simultaneously working with several number systems, the base is indicated as a subscript. Thus, 503 = 503 10 .
In addition to the decimal system, the 2nd, 8th, and 16th systems deserve special attention.
Binary number system
This system is mainly used in computer technology. Why didn’t you use the 10th familiar to us? The first computing machine was created by Blaise Pascal, who used a decimal system in it, which turned out to be inconvenient in modern electronic machines, because it required the production of devices capable of operating in 10 states, which increased their price and the total size of the machine. These drawbacks are deprived of elements operating in the 2nd system. Nevertheless, the system in question was created long before the invention of computers and goes back to the Inca civilization, where a pile of complex rope plexuses and knots were used.
The binary positional number system has a base of 2 and uses 2 characters (digits) to write the number 2: 0 and 1. In each digit, only one digit is allowed - either 0 or 1. The
number 101 can be an example. It is similar to the number 5 in the decimal number system . In order to transfer from the 2nd to the 10th it is necessary to multiply each digit of the binary number by the base “2”, raised to a power equal to the category. Thus, the number 101 2 = 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5 10 .
Well, for machines the 2nd number system is more convenient, but we often see, we use numbers in the 10th system on the computer. How then does the machine determine which digit the user enters? How does a number translate from one system to another, because it has only 2 characters at its disposal - 0 and 1?
In order for a computer to work with binary numbers (codes), they must be stored somewhere. To store each individual digit, a trigger is used, which is an electronic circuit. It can be in 2 states, one of which corresponds to zero, the other to unity. To remember a single number, a register is used - a group of triggers, the number of which corresponds to the number of bits in a binary number. And the set of registers is RAM. The number contained in the register is a machine word. Arithmetic and logical operations with words are carried out by an arithmetic-logical device (ALU). To simplify access to the registers, they are numbered. The number is called the register address. For example, if you need to add 2 numbers, it is enough to indicate the numbers of cells (registers) in which they are located, and not the numbers themselves. Addresses are written in 8- and hexadecimal systems (they will be described below), since the transition from them to the binary system and vice versa is quite simple. To transfer from the 2nd to the 8th, it is necessary to divide into groups of 3 digits from right to left, and to go to the 16th, to 4. If the digits do not reach the digits in the leftmost group, they are filled with zeros on the left, which are called zeros leading. As an example, take the number 1011002 . In octal it is 101 100 = 54 8 , and in hexadecimal it is 0010 1100 = 2С 16 . Great, but why do we see decimal numbers and letters on the screen? When a key is pressed, a certain sequence of electrical pulses is transmitted to the computer, with each symbol having its own sequence of electrical pulses (zeros and ones). The keyboard and screen driver program accesses the character code table (for example, Unicode, which allows you to encode 65536 characters), determines which character the received code corresponds to and displays it on the screen. Thus, the texts and numbers are stored in binary memory in the computer's memory, and programmatically converted to images on the screen.
Octal number system
The 8th number system, like binary, is often used in digital technology. It has a base of 8 and uses digits from 0 to 7 to record the number.
An example of an octal number: 254. To transfer to the 10th system, each digit of the original number must be multiplied by 8 n , where n is the number of the digit. It turns out that 254 8 = 2 * 8 2 + 5 * 8 1 + 4 * 8 0 = 128 + 40 + 4 = 172 10 .
Hexadecimal notation
The hexadecimal system is widely used in modern computers, for example, using it, the color is indicated: #FFFFFF - white color. The system in question has a base of 16 and uses to write the numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, where the letters are 10, 11, 12, 13, 14, 15, respectively.
Take 4F5 16 as an example . To translate into the octal system, first convert the hexadecimal number to binary, and then, breaking into groups of 3 digits, into octal. To convert a number to 2nd, each digit must be represented as a 4-bit binary number. 4F5 16 = (100 1111 101) 2. But there is no discharge in groups 1 and 3, so fill each with leading zeros: 0100 1111 0101. Now you need to divide the resulting number into groups of 3 digits from right to left: 0100 1111 0101 = 010 011 110 101. We translate each binary group into an octal system, multiplying each bit by 2 n , where n is the bit number: (0 * 2 2 + 1 * 2 1 + 0 * 2 0 ) (0 * 2 2 + 1 * 2 1 + 1 * 2 0 ) (1 * 2 2 + 1 * 2 1 + 0 * 2 0 ) (1 * 2 2 + 0 * 2 1 + 1 * 2 0 ) = 2365 8 .
In addition to the considered positional number systems, there are others, for example:
1) Trinitarian
2) Quaternary
3) Duodecimal
Positional systems are divided into homogeneous and mixed.
Homogeneous positional number systems
The definition given at the beginning of the article adequately describes homogeneous systems, so the refinement is unnecessary.
Mixed number systems
We can add the theorem to the above definition: “if P = Q n (P, Q, n are positive integers, and P and Q are bases), then the notation of any number in the mixed (PQ) number system identically coincides with by writing the same number in the number system with the base Q. ”
Based on the theorem, we can formulate the rules for the transfer from the Pth to the Qth system and vice versa:
- To transfer from the Qth to the Pth, you need a number in the Qth system, split into groups of n digits, starting with the right digit, and replace each group with one digit in the Pth system.
- To transfer from the Pth to the Qth, it is necessary to convert each digit of the number in the Pth system to the Qth and fill in the missing digits with leading zeros, with the exception of the left, so that each number in the system with the base Q consists of n digits .
A striking example is the conversion from binary to octal. Let's take the binary number 10011110 2 , to convert it to octal, we divide it from right to left into groups of 3 digits: 010 011 110, now multiply each digit by 2 n , where n is the digit number, 010 011 110 = (0 * 2 2 +1 * 2 1 + 0 * 2 0 ) (0 * 2 2 + 1 * 2 1 + 1 * 2 0 ) (1 * 2 2 + 1 * 2 1 + 0 * 2 0 ) = 236 8 . It turns out that 10011110 2 = 236 8 . For the uniqueness of the image of the binary octal number, it is divided into triples: 236 8= (10 011 110) 2-8 .
Mixed number systems are also, for example:
1) Factorial
2) Fibonacci
Transfer from one number system to another
Sometimes it is necessary to convert a number from one number system to another, therefore, we consider the methods of translation between different systems.
Convert to Decimal
There is a number a 1 a 2 a 3 in the number system with base b. To transfer to the 10th system, it is necessary to multiply each bit of the number by b n , where n is the number of the bit. Thus, (a 1 a 2 a 3 ) b = (a 1 * b 2 + a 2 * b 1 + a 3 * b 0 ) 10 .
Example: 101 2 = 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5 10
Convert from decimal to other
The whole part:
- We successively divide the integer part of the decimal number by the base of the system into which we translate until the decimal number becomes zero.
- Residues obtained by division are the numbers of the desired number. The number in the new system is written starting from the last remainder.
Fractional part:
- The fractional part of the decimal number is multiplied by the base of the system into which you want to translate. Separate the whole part. We continue to multiply the fractional part by the base of the new system until it becomes equal to 0.
- The numbers in the new system are the whole parts of the multiplication results in the order corresponding to their receipt.
Example: translate 15 10 to octal:
15 \ 8 = 1, remainder 7
1 \ 8 = 0, remainder 1
Having written down all the rests from bottom to top, we get the final number 17. Therefore, 15 10 = 17 8 .
Binary to octal and hexadecimal conversion
To convert to octal, we divide the binary number into groups of 3 digits from right to left, and fill in the missing extreme digits with leading zeros. Next, we transform each group by sequentially multiplying the digits by 2 n , where n is the number of the digit.
As an example, take the number 1001 2 : 1001 2 = 001 001 = (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ) (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ) = (0+ 0 + 1) (0 + 0 + 1) = 11 8
For translation into hexadecimal, we divide the binary number into groups of 4 digits from right to left, then - similarly, from the 2nd to the 8th.
Convert from octal and hexadecimal to binary
Translation from octal to binary - we convert each digit of the octal number to binary 3-digit number by dividing by 2 (for more details on dividing, see the section “Converting from decimal number system to others” above), fill in the missing extreme digits with leading zeros.
For example, consider the number 45 8 : 45 = (100) (101) = 100101 2
Transfer from the 16th to the 2nd - we convert each digit of the hexadecimal number into a binary 4-digit number by dividing by 2, fill in the missing extreme digits with leading zeros .
Conversion of the fractional part of any number system to decimal
Conversion is carried out as for the whole parts, except that the digits of the number are multiplied by the base to the power of “-n”, where n starts from 1.
Example: 101.011 2 = (1 * 2 2 + 0 * 2 1 + 1 * 2 0 ), (0 * 2 -1 + 1 * 2 -2 + 1 * 2 -3 ) = (5), (0 + 0 , 25 + 0.125) = 5.375 10
Converting the fractional part of the binary system to the 8th and 16th
The fractional part is translated in the same way as for the integer parts of the number, with the exception of the fact that the breakdown into groups of 3 and 4 digits goes to the right of the decimal point, the missing digits are supplemented with zeros on the right.
Example: 1001.01 2 = 001 001, 010 = (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ) (0 * 2 2 + 0 * 2 1 + 1 * 2 0 ), (0 * 2 2 + 1 * 2 1 + 0 * 2 0 ) = (0 + 0 + 1) (0 + 0 + 1), (0 + 2 + 0) = 11.2 8
Convert the fractional part of the decimal system to any other
To translate the fractional part of a number into other number systems, you need to turn the integer part to zero and start multiplying the resulting number by the base of the system into which you want to translate. If as a result of multiplication the integer parts appear again, they must be turned back to zero, having previously memorized (written down) the value of the resulting integer part. The operation ends when the fractional part is completely zero.
For example, we translate 10.625 10 into the binary system:
0.625 * 2 = 1.25
0.250 * 2 = 0.5
0.5 * 2 = 1.0
Having written down all the residuals from top to bottom, we get 10.625 10 = (1010), (101) = 1010,101 2
