Naive Bayesian classifier in 25 lines of code
The naive Bayesian classifier is one of the simplest classification algorithms. However, very often it works no worse, or even better, than more complex algorithms. Here I want to share the code and a description of how this all works.
And so, for example, take the task of determining gender by name. Of course, to determine the gender, you can create a large list of names with gender labels. But this list will in any case be incomplete. In order to solve this problem, you can “train” the model using marked names.
If interested, please.
Suppose we have a line of text O. In addition, there are classes C, one of which we must include a line. We need to find a class c in which its probability for a given string would be maximum. Mathematically, this is written as follows:

Calculating P (C | O) is difficult. But you can use the Bayesian theorem and proceed to indirect probabilities:
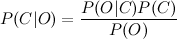
Since we are looking for the maximum of a function, the denominator does not interest us (it is a constant in this case). In addition, you need to look at line O. Usually, it makes no sense to work with the entire line. It is much more efficient to isolate certain features from it. Thus, the formula will take the form: The

denominator does not interest us. The numerator can be rewritten as follows.

But this is again difficult. Here we include the “naive” assumption that the variables O depend only on the class C, and do not depend on each other. This is a lot of simplification, but often it works. The numerator will take the form:

The final formula will take the form:
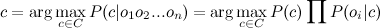 (1)
(1)
i.e. all you need to do is calculate the probabilities P (C) and P (O | C). The calculation of these parameters is called the training of the classifier.
Below is the python code. It contains only two functions: one for training (counting the parameters of the formula), the other for classification (direct calculation of the formula).
In the train function, the first five lines count the number of classes C, as well as the frequency of occurrence of features O and C in one sample. The second part of the method simply normalizes these frequencies. Thus, the probabilities P © and P (O | C) are obtained at the output.
The classify function searches for the most likely class. The only difference from formula (1) is that I replace the product of the probabilities with the sum of the logarithms taken with a negative sign, and I calculate not argmax, but argmin. Switching to logarithms is a common technique to avoid too small numbers that could have been obtained by multiplying probabilities.
The number 10 (^ - 7), which is substituted into the logarithm, is a way to avoid zero in the argument of the logarithm (since it will otherwise be undefined).
To train the classifier we take a marked-up list of male and female names and use this code:
The file 'names.txt' can be downloaded here .
As a feature, I chose the last letter of the name (see the get_features function). It works well, but for the working version it is better to use a more complicated scheme. For example, select the first letter of the name and the last two. For example, like this:
The algorithm can be used for any number of classes. For example, you can try to build a classifier of texts by emotional coloring.
I tested the classifier on parts of the original case with names. The accuracy was 96%. This is not a brilliant result, but for many tasks it’s quite enough.
And so, for example, take the task of determining gender by name. Of course, to determine the gender, you can create a large list of names with gender labels. But this list will in any case be incomplete. In order to solve this problem, you can “train” the model using marked names.
If interested, please.
Bit of theory
Suppose we have a line of text O. In addition, there are classes C, one of which we must include a line. We need to find a class c in which its probability for a given string would be maximum. Mathematically, this is written as follows:

Calculating P (C | O) is difficult. But you can use the Bayesian theorem and proceed to indirect probabilities:
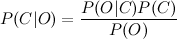
Since we are looking for the maximum of a function, the denominator does not interest us (it is a constant in this case). In addition, you need to look at line O. Usually, it makes no sense to work with the entire line. It is much more efficient to isolate certain features from it. Thus, the formula will take the form: The

denominator does not interest us. The numerator can be rewritten as follows.

But this is again difficult. Here we include the “naive” assumption that the variables O depend only on the class C, and do not depend on each other. This is a lot of simplification, but often it works. The numerator will take the form:

The final formula will take the form:
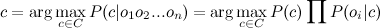 (1)
(1) i.e. all you need to do is calculate the probabilities P (C) and P (O | C). The calculation of these parameters is called the training of the classifier.
The code
Below is the python code. It contains only two functions: one for training (counting the parameters of the formula), the other for classification (direct calculation of the formula).
from __future__ import division
from collections import defaultdict
from math import log
def train(samples):
classes, freq = defaultdict(lambda:0), defaultdict(lambda:0)
for feats, label in samples:
classes[label] += 1 # count classes frequencies
for feat in feats:
freq[label, feat] += 1 # count features frequencies
for label, feat in freq: # normalize features frequencies
freq[label, feat] /= classes[label]
for c in classes: # normalize classes frequencies
classes[c] /= len(samples)
return classes, freq # return P(C) and P(O|C)
def classify(classifier, feats):
classes, prob = classifier
return min(classes.keys(), # calculate argmin(-log(C|O))
key = lambda cl: -log(classes[cl]) + \
sum(-log(prob.get((cl,feat), 10**(-7))) for feat in feats))
In the train function, the first five lines count the number of classes C, as well as the frequency of occurrence of features O and C in one sample. The second part of the method simply normalizes these frequencies. Thus, the probabilities P © and P (O | C) are obtained at the output.
The classify function searches for the most likely class. The only difference from formula (1) is that I replace the product of the probabilities with the sum of the logarithms taken with a negative sign, and I calculate not argmax, but argmin. Switching to logarithms is a common technique to avoid too small numbers that could have been obtained by multiplying probabilities.
The number 10 (^ - 7), which is substituted into the logarithm, is a way to avoid zero in the argument of the logarithm (since it will otherwise be undefined).
To train the classifier we take a marked-up list of male and female names and use this code:
def get_features(sample): return (sample[-1],) # get last letter
samples = (line.decode('utf-8').split() for line in open('names.txt'))
features = [(get_features(feat), label) for feat, label in samples]
classifier = train(features)
print 'gender: ', classify(classifier, get_features(u'Аглафья'))
The file 'names.txt' can be downloaded here .
As a feature, I chose the last letter of the name (see the get_features function). It works well, but for the working version it is better to use a more complicated scheme. For example, select the first letter of the name and the last two. For example, like this:
def get_features(sample): return (
'll: %s' % sample[-1], # get last letter
'fl: %s' % sample[0], # get first letter
'sl: %s' % sample[1], # get second letter
)
The algorithm can be used for any number of classes. For example, you can try to build a classifier of texts by emotional coloring.
Tests
I tested the classifier on parts of the original case with names. The accuracy was 96%. This is not a brilliant result, but for many tasks it’s quite enough.
