Discrete mathematics in "everyday" application
In yesterday’s series, the futurams posed a rather interesting task - I could not help but disassemble it here.

So, the plot is as follows: The professor invented a machine for exchanging bodies, which, as it turned out, works only in one direction. After several permutations, the heroes found themselves in a difficult situation in which they had to come up with a way to return back to their bodies. This is where “pure mathematics” will help us .
So let's get started. Let be a cycle of length k on the set [n] = {1 ... n} . Without loss of generality, we write:
a cycle of length k on the set [n] = {1 ... n} . Without loss of generality, we write:

Now let (a, b) be a transposition that swaps the contents of a and b .
By assumption, obtained using certain permutations over [n] .
obtained using certain permutations over [n] .
We introduce two “new bodies” {x, y} and write

For any i = 1, ... k, we write it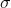 as a series of permutations:
as a series of permutations:
(x,2)...(x,i))((y,i+1)(y,i+2)(y,k))((x,i+1))((y,1)))
Note that transpositions change an element from [n] with some element from {x, y} , therefore, all transpositions differ from the ones that formed the original permutation , as well as from the transposition (x, y) . A simple check gives:
, as well as from the transposition (x, y) . A simple check gives:

Thus, it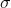 inverts a cycle of length k , leaving x and y rearranged without using transposition (x, y) .
inverts a cycle of length k , leaving x and y rearranged without using transposition (x, y) .
Now let be a random substitution; it splits into a composition of independent cycles, each of which can be inverted using the algorithm obtained above, after which, if necessary, you can swap x and y using the transposition (x, y) .
be a random substitution; it splits into a composition of independent cycles, each of which can be inverted using the algorithm obtained above, after which, if necessary, you can swap x and y using the transposition (x, y) .
So that. And you say that discrete does not have IRL applications.

So, the plot is as follows: The professor invented a machine for exchanging bodies, which, as it turned out, works only in one direction. After several permutations, the heroes found themselves in a difficult situation in which they had to come up with a way to return back to their bodies. This is where “pure mathematics” will help us .
So let's get started. Let be
 a cycle of length k on the set [n] = {1 ... n} . Without loss of generality, we write:
a cycle of length k on the set [n] = {1 ... n} . Without loss of generality, we write:
Now let (a, b) be a transposition that swaps the contents of a and b .
By assumption,
 obtained using certain permutations over [n] .
obtained using certain permutations over [n] . We introduce two “new bodies” {x, y} and write

For any i = 1, ... k, we write it
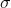 as a series of permutations:
as a series of permutations:(x,2)...(x,i))((y,i+1)(y,i+2)(y,k))((x,i+1))((y,1)))
Note that transpositions change an element from [n] with some element from {x, y} , therefore, all transpositions differ from the ones that formed the original permutation
 , as well as from the transposition (x, y) . A simple check gives:
, as well as from the transposition (x, y) . A simple check gives:
Thus, it
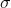 inverts a cycle of length k , leaving x and y rearranged without using transposition (x, y) .
inverts a cycle of length k , leaving x and y rearranged without using transposition (x, y) . Now let
 be a random substitution; it splits into a composition of independent cycles, each of which can be inverted using the algorithm obtained above, after which, if necessary, you can swap x and y using the transposition (x, y) .
be a random substitution; it splits into a composition of independent cycles, each of which can be inverted using the algorithm obtained above, after which, if necessary, you can swap x and y using the transposition (x, y) . So that. And you say that discrete does not have IRL applications.
