Driving a vehicle using a neural network

annotation

Using a neural network, we want the vehicle to control itself, avoiding obstacles. We achieve this by selecting the appropriate inputs / outputs and thorough training of the neural network. We feed the distance networks to the nearest obstacles around the car, simulating the vision of a human driver. At the output, we obtain the acceleration and rotation of the steering wheel of the vehicle. We also need to train the network on a variety of I / O strategies. The result is impressive even with just a few neurons! A car drives around obstacles, but it is possible to make some modifications so that this software tool copes with more specific tasks.

Introduction

The idea is to have a vehicle that drives itself and avoids obstacles in the virtual world. Every moment it decides for itself how to change its speed and direction depending on the environment. In order to make this more real, the AI ​​needs to see only what a person would see if they were driving, so the AI ​​will only make decisions based on the obstacles that are in front of the vehicle. With realistic input, the AI ​​could be used in a real car and work just as well.
When I hear the phrase: "Driving a vehicle using AI," I immediately think about computer games. Many of the racing games can use this technique to control vehicles, but there are a number of other applications that are looking for a means of transport control in a virtual or real world.
So how are we going to do this? There are many ways to implement AI, but if we need a “brain” to control a vehicle, then neural networks will do just fine. Neural networks work just like our brain. They will probably be the right choice. We must determine what will be the input and the output of our neural network.

Neural networks

Neural networks appeared when studying the structure of the brain. Our brain consists of 10 ¹¹ neuron cells that send electrical signals to each other. Each neuron consists of one or two axons that “produce the result”, and a large number of dendrites that receive input electrical signals. A neuron needs a certain input signal strength, which is added up from all dendrites in order to be activated. Once activated, a neuron sends an electrical signal down its axon to other neurons. Connections (axons and dendrites) are strengthened if they are often used.
This principle is applied in smaller neural networks. Modern computers do not have the computing power that creates twenty billion neurons, but even with several neurons, a neural network can give a reasonable answer.
Neurons are organized into layers, as shown in Figure 1 . The input layer will have inputs, and depending on the strength of the connection with each neuron in the next layer, the input signal is supplied to the next level. The strength of the joint is called weight. The value of each neuron in each layer will depend on the weight of the connection and the value of the neurons of the previous layer.

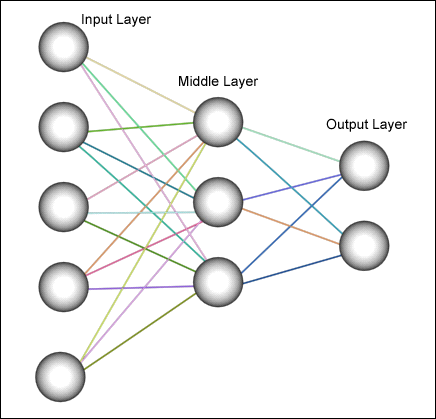
Picture 1
The driver can be compared with the "function". There are many inputs: what the driver sees. This data is processed by the brain as a function, and the driver’s reaction is the way out of the function.
The function f (x) = y converts the value of x (one dimension) into y (one dimension).
We use a backpropagation neural network for the driver’s brain, since such neural networks are able to approximate any function with areas of definition and values ​​that can have several dimensions: F (x1, x2, ..., xn) = y1, y2, ... , yn .
This is exactly what we need, since we must work with several inputs and outputs.
When a neural network consists of only a few neurons, we can calculate the weights necessary to obtain an acceptable result. But as the number of neurons increases, so does the complexity of the calculations. The backpropagation network can be trained to establish the necessary weights. We just have to provide the desired results with their corresponding inputs.
After training, the neural network will respond to produce a result close to what you want when applying a known result, and “guess” the correct answer for any input that does not match the training.
Actual calculations are beyond the scope of this article. There are many good books explaining how backward propagation networks work.
The neural network used in this case has 4 layers ( Fig. 2) I tried various combinations from three to six layers. Everything worked fine with three layers, but when I trained the network on a set of twenty-two inputs / outputs, the approximation of the function was not accurate enough. Five and six layers did their job perfectly, but it took a lot of time to learn (from 20 to 30 minutes in PII), and when I started the program, it took a lot of processor time to calculate.
In this network, three neurons in the input layer and two in the resulting layer. I will explain why later. Between them two layers of eight neurons in each. Again, I tested a layer with a larger and smaller number of neurons and settled on eight, since this number gives an acceptable result.
When choosing the number of neurons, keep in mind that each layer and each neuron added to the system will increase the time required to calculate the weights.

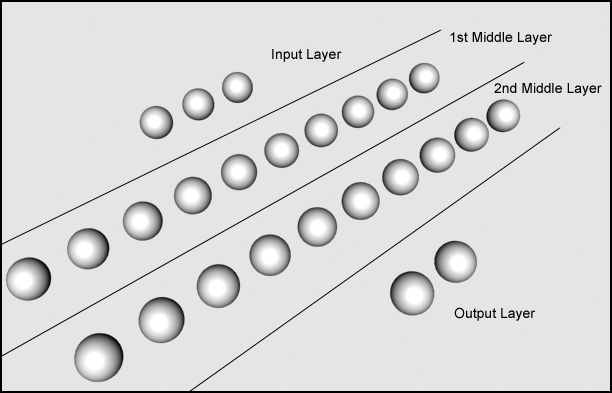
Figure 2
Addition of neurons:
We have an input layer I with i neurons, and a resulting layer O with o neurons. We want to add a single neuron in the middle layer M . The number of connections between neurons that we add is (i + o) .
Adding layers:
We have an input layer I with i neurons, and the resulting layer O with o neurons. We want to add Mlayers with m neurons in each. The number of connections between neurons that we add is (m * (i + o)) .
Now that we have examined how the “brain” works, we need to understand how to determine the inputs and outputs of the neural network. A neural network in itself does nothing if we give it information from the virtual world and do not give the network response to the vehicle controller.

entrance

What information is important for driving? First, we must know the position of the obstacle in relation to us. Is this position on the right, on our left, or in front of us? If there are buildings on either side of the road, but there is nothing ahead, we speed up. But if the car stopped in front of us, we brake. Secondly, we need to know the distance from our position to the object. If the object is far away, we will continue to move until it approaches, in which case, we slow down or stop.
This is exactly the information that we will use for our neural network. For simplicity, we introduce three relative directions: left, front, and right. As well as the distance from the obstacle to the vehicle.

Figure 3
Define the field of view of our AI driver and make a list of objects that he sees. For simplicity, we use a circle in our example, but we could use a real cone truncated by six intersecting planes. Now for each object in this circle, we check whether it is in the left field of view, right, or in the center.
An array is supplied to the entrance to the neural network: float Vision [3] . The distances to the nearest obstacle to the left, in the center, and to the right of the vehicle will be stored in Vision [0] , Vision [1] and Vision [2] respectively. In figure 3shown how this array looks. The obstacle on the left is 80% of the maximum distance, on the right is 40%, and there are no obstacles in the center.
In order to calculate this, we need the position (x, y) of each object, the position (x, y) of the car and the angle of the vehicle. We also need r (circle radius) and d _right , d _left - vectors between the car and the lines L _right and L _left . These lines are parallel to the direction of movement of the car. Both vectors are perpendicular to the lines.
Although this is a 3D world, all mathematics is two-dimensional, since a car cannot move in the third dimension because it does not fly. All equations include only x and y , but not z .
First, we calculate the equations of the lines L _right and L _left , which will help us determine whether an obstacle is located to the right, left or in the center of the vehicle.
Figure 4 is an illustration of all the calculations.

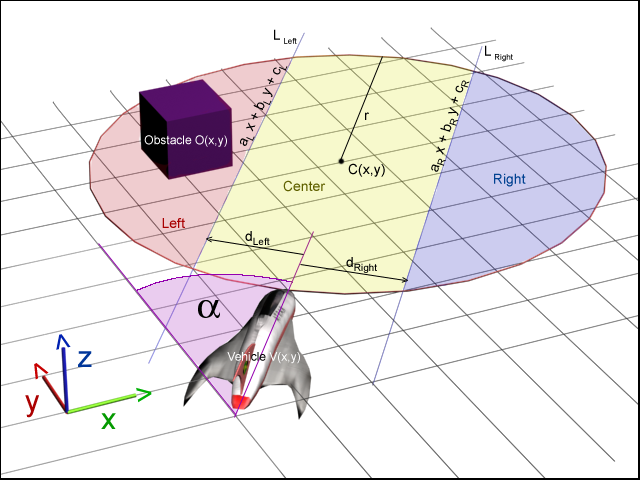
Figure 4

where

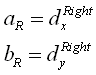
Then we calculate the coordinates of the point on the line

where V _x and V are _the vehicle position.
Now we can finally calculatec _r

Similarly, we find the equation of the line L _left using the vector d _left .
Next, we need to calculate the center of the circle. Everything inside the circle will be seen by AI. The center of the circle C (x, y) at a distance r from the position of the vehicle V (x, y) .


where V _x , V _{y the} position of the vehicle and C _x , C _y - the center of the circle.
Then we check whether each object in the world is within a circle (if the objects are organized in a quad-tree or an octree, this process is much faster than a linked list).
If 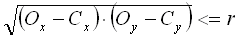, then the object is in a circle, where O _x , O _{y are the} coordinates of the obstacle.
For each object within the circle, we must check whether it is located to the right, left, or center of the vehicle.
If , then the object is on the right side of the circle;
otherwise, if , then on the left side it is
otherwise centered.
We calculate the distance from the object to the car.

Now we save the distance in the corresponding part of the array ( Vision [0] ,Vision [1] or Vision [2] ) provided that the previously stored distance is greater than the just calculated one. Initially, the Vision array must be initialized with 2r values .
After checking each object, we have a Vision array with distances to the nearest objects to the right, in the center and to the left of the car. If no objects were found in this field of view, the array element will have a default value , which means: "there is no object within visibility."
Since the neural network uses a sigmoid function, the input must be between 0.0 and 1.0 . 0,0will mean that the object is touching the vehicle and 1.0 means that there are no objects within sight. Since we set the maximum distance that the AI ​​driver can see, we can easily bring all distances to a range from 0.0 to 1.0 .

Exit

At the exit, we should receive instructions for changing the speed of the car and direction. It can be acceleration, braking and steering angle. So we need two exits; one will be the acceleration / deceleration value (braking is simply negative acceleration), and the other will indicate a change in direction.
The result is between 0.0 and 1.0 for the same reason as the input. For acceleration, 0.0 means "full brake"; 1.0 - “full throttle” and 0.5 - no braking or acceleration. For steering, 0.0 means “all the way to the left,” 1.0 means “all the way to the right,” and 0.5- do not change direction. So we have to translate the results into values ​​that we can use.


It should be noted that “negative acceleration” means braking if the vehicle is moving forward, but it also means moving in the opposite direction if the vehicle is at rest. In addition, “positive acceleration” means braking if the vehicle is traveling in the opposite direction.

Training

As I mentioned earlier, we must first train the neural network. We need to create a set of inputs and their corresponding outputs.
Choosing the right I / O to train a neural network is probably the hardest part of the job. I had to train a network with a lot of data, watch how the car acted in the environment, and then change the records as needed. Depending on how we train the network, the vehicle may “wobble” in some situations and become immobilized.
We compile a table ( table. 1 ) of various positions of obstacles relative to the vehicle and the desired AI response.
Table 1

Input Neurons Relative Distance to Obstacle			Output neurons
Left	In the center	On right	Acceleration	Direction
No obstacles	No obstacles	No obstacles	Full throttle	Straight
Half way	No obstacles	No obstacles	Slight acceleration	A bit to the right
No obstacles	No obstacles	Half way	Slight acceleration	To the left
No obstacles	Half way	No obstacles	Braking	To the left
Half way	No obstacles	Half way	Acceleration	Straight
Object touch	Object touch	Object touch	Return stroke	To the left
Half way	Half way	Half way	Without changes	To the left
Object touch	No obstacles	No obstacles	Braking	Full right
No obstacles	No obstacles	Object touch	Braking	Full left
No obstacles	Object touch	No obstacles	Return stroke	To the left
Object touch	No obstacles	Object touch	Full throttle	Straight
Object touch	Object touch	No obstacles	Return stroke	Full right
No obstacles	Object touch	Object touch	Return stroke	Full left
Object close	Object close	Object is very close	Without changes	To the left
Object is very close	Object close	Object close	Without changes	To the right
Object touch	Object is very close	Object is very close	Braking	Full right
Object is very close	Object is very close	Object touch	Braking	Full left
Object touch	Object Close	Far Object	Without changes	To the right
Object far	Object close	Object touch	Without changes	To the left
Object is very close	Object close	The subject is closer than halfway	Without changes	Full right
The subject is closer than halfway	Object close	Object is very close	Braking	Full left

And now you can translate this into the numbers in table 2 .
table 2

Input neurons			Output neurons
Left	In the center	On right	Acceleration	Direction
1,0	1,0	1,0	1,0	0.5
0.5	1,0	1,0	0.6	0.7
1,0	1,0	0.5	0.6	0.3
1,0	0.5	1,0	0.3	0.4
0.5	1,0	0.5	0.7	0.5
0,0	0,0	0,0	0.2	0.2
0.5	0.5	0.5	0.5	0.4
0,0	1,0	1,0	0.4	0.9
1,0	1,0	0,0	0.4	0.1
1,0	0,0	1,0	0.2	0.2
0,0	1,0	0,0	1,0	0.5
0,0	0,0	1,0	0.3	0.8
1,0	0,0	0,0	0.3	0.2
0.3	0.4	0.1	0.5	0.3
0.1	0.4	0.3	0.5	0.7
0,0	0.1	0.2	0.3	0.9
0.2	0.1	0,0	0.3	0.1
0,0	0.3	0.6	0.5	0.8
0.6	0.3	0,0	0.5	0.2
0.2	0.3	0.4	0.5	0.9
0.4	0.3	0.2	0.4	0.1

Entrance:
0,0: The object is almost touching the vehicle.
1.0: Object at the maximum distance from the car or no object in the field of view
Exit:
Acceleration
0.0: Maximum negative acceleration (braking or vice versa)
1.0: Maximum positive acceleration
Direction
0.0: Full left
0.5: Straight
1.0: Full Right

Conclusion / Ways to improve

The use of a backpropagation neural network is suitable for our purposes, but there are some problems identified during testing. Some changes could make the program more reliable and adapt it to other situations. Now I will describe to you some problems that you might think about solving.

Figure 5
The vehicle “gets stuck” for a while, because it is hesitant in deciding whether to go left or right. This was to be expected: people sometimes have the same problem. It is not so easy to fix this, trying to adjust the weights of the neural network. But we can add a line of code that says:
"If (the vehicle does not move for 5 seconds), then (take control and turn it 90 degrees to the right)."
In this way, we can guarantee that the car never stands still, not knowing what to do.
The vehicle will not see a small gap between the two houses, as shown in Figure 5 . Since we do not have a high level of accuracy in vision (left, center, right), two buildings that are close to each other will look like a wall for artificial intelligence. In order to have a clearer view of our AI, we need to have 5 or 7 levels of accuracy at the entrance to the neural network. Instead of “right, center, left,” we could have “far right, near right, center, near left, far left.” With good neural network training, artificial intelligence will see the gap and understand that it can pass through it.
It works in a 2D world, but what if a vehicle is able to fly through a cave? With some changes to this technique, we can make the AI ​​fly, not ride. By analogy with the last problem, we increase the accuracy of the gaze. But instead of adding “rights” and “lion”, we can do as shown in table 3 .
Table 3

Top left	Up	Top right
Left	Center	On right
Bottom left	Down below	Bottom right

Now that our neural network can see the world in 3D, we just need to change our control and the reaction of the vehicle to the world.
The vehicle only "wanders" without any specific purpose. It does nothing but avoid obstacles. Depending on where we want to go, we can "tune" the brain as needed. We can have many different neural networks and use the right one in a specific situation. For example, we could follow a car in sight. We just need to connect another neural network trained to follow another vehicle, receiving the location of the second vehicle as input.
As we just saw, this method can be improved and applied in various fields. Even if it is not used for any useful purpose, it will still be interesting for us to observe how the artificial intelligence system behaves in the environment. If we observe for a sufficiently long time, we will understand that in difficult conditions, a vehicle will not always follow the same path due to a small difference in solution due to the nature of the neural network. A car will sometimes drive to the left of the building, and sometimes to the right of the same building.

Literature

1. Joey Rogers, Object-Oriented Neural Network in C ++, Academic Press, San Diego, CA, 1997
2. MT Hagan, HB Demuth and MH Beale, Neural Network Design, PWS Publishing, Boston, MA, 1995