L-systems. Tree modeling
 The post is a free translation of the second chapter of the book “Algorithmic Beauty of Plants” by Przemyslaw Pruschinkiewicz and Aristid Lindenmeyer (The Algorithmic Beauty of Plants, Aristid Lindenmayer, Przemyslaw Prusinkiewicz), and is a continuation of the wonderful article “ L-Systems - The Mathematical Beauty of Plants ” valyard (thanks to him for inspiration :)
The post is a free translation of the second chapter of the book “Algorithmic Beauty of Plants” by Przemyslaw Pruschinkiewicz and Aristid Lindenmeyer (The Algorithmic Beauty of Plants, Aristid Lindenmayer, Przemyslaw Prusinkiewicz), and is a continuation of the wonderful article “ L-Systems - The Mathematical Beauty of Plants ” valyard (thanks to him for inspiration :)The first models.
Computer modeling of tree branching processes has a relatively long history. The first model proposed by Ulam was based on the concept of cellular automata developed by von Neumann. The branching process was carried out by iterations, and began with one stained cell on a triangular grid, then those that touched one and only one vertex of cells stained in the previous iteration were stained.
Further, this idea was developed. Meinhardt replaced the triangular grid with a square one, and used the resulting cell space to test the biological hypotheses of the formation of network structures. In addition to the clean branching process, his model took into account the effects of reconnections or anastomoses that could occur between leaves or veins, for example. Green rewrote the cellular automaton for three dimensions and simulated growth processes that took into account the environment. For example, Figure 2.1 shows the growth of a vine over a house. Cohen's models took into account the concept of “field density” in the rules of growth, which turned out to be better than, for example, working with discrete cells. Figure 2.1. Harmonious Green architecture.

A common feature of these approaches is the emphasis on the interaction, both between different elements of the structure, and structure with the environment. And although this interaction obviously affects the growth of real plants, its modeling is a very difficult task. Therefore, simple models that ignore even such fundamental things as a collision between branches are more common today.
Honda model.
Honda proposed the first model in the simple category, and made the following assumptions:
- tree segments are straight, their cross-sectional area is not considered;
- during the iteration, the parent segment produces two subsidiaries;
- the length of two daughter segments is shorter than the parent in
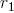 and
and 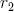 times;
times; - the parent segment and its two subsidiaries are in the same branch plane . The child segments exit the maternal at branching angles
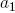 and
and 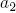 ;
; - in connection with the action of gravitational force, the branch plane is “closest to the horizontal plane”, in other words, the line perpendicular to the mother segment and lying in the plane of the branch is horizontal. An exception is made for branches attached to the main trunk. In this case, a constant angle of divergence is used
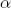 .
.
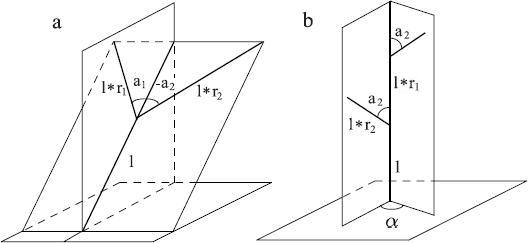
Figure 2.2. The geometry of the tree according to Honda.
By varying the numerical parameters, Honda received a wide variety of tree-like forms. With some improvements, his models were applied to the study of branching processes of real trees. Subsequently, different rules were proposed for branch angles, in order to also cover tree structures in which the planes of further branches are perpendicular to each other. Honda's results served as the basis for the models proposed by Eono and Kuniai. They proposed several improvements, the most important of which was the rotation of segments in certain directions, corresponding to the tendency of the branches to the sun, taking into account wind and gravity. A similar concept was proposed by Cohen, while Refai and Armstrong developed a more physically accurate method for bending branches.
Honda, Eono, and Kuniai models used straight lines of constant or variable width to construct a “wood skeleton." A significant improvement in the photorealism of the synthesized models was achieved by Blumenfel and Oppenheimer, who presented bending branches, carefully simulated the surfaces around the branch nodes, and applied textures to the bark and leaves (Figure 2.3) Figure 2.3. Blumenfel, Acer graphics. In the work of Honda, the branch structure was constructed according to deterministic algorithms. In contrast, stochastic laws were used in a group of models proposed by Reeves and Blau, de Refai, Remfrey, Neil, and Steves. Although these models are constructed differently, they share the general paradigm of describing the structure of trees, in particular, the calculation of capabilities

the formation of branches. Reeves and Blau sought not to delve into the biological details of the simulated structures (Figure 2.4). On the contrary, de Refay used a stochastic approach to create realistic plants and simulated the activity of buds at discrete points in time. Having received a timer signal, the kidney could either:
- nothing to do;
- become a flower;
- become a segment of the stem ending in a new vertex and one or more lateral branches of the stem;
- die or disappear.
These events occurred according to stochastic laws, described separately for each plant species. Geometric parameters, such as the length and diameter of the stem segment, branch angles, were also calculated according to stochastic algorithms. Figure 2.4. Picture of the forest, Reeves, © 1984 Pixar. Figure 2.5. Oil palm canopy, CIRAD Modelisation Laboratory.


Using the basic types of development laws in this method, Helle, Oldman, and Tomlinson established 23 different types of tree architecture. Detailed models of selected plant types have been developed and described in the literature. A simple tree model is shown in Figure 2.5. Remfrey's approach was similar to that of De Refay, but the former used longer time intervals. It turned out that in order to achieve reliable results, stochastic models should describe the behavior of lateral sprouts that is possible during the year.
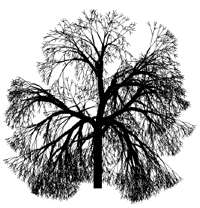
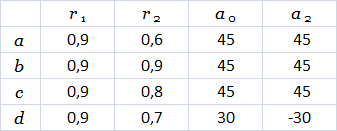
The use of L-systems to generate trees was first considered by Eono and Kuniai. To begin with, based on the formal definition of L, they proved its unsuitability for modeling higher plants. But the proof did not apply to parametric L-systems with a tortoise interpretation of strings. For example, the L-systems in Figure 2.6 implements those Honda models in which one of the branch angles is zero, a pliable monopodial structure and clearly defined main and lateral axes. Figure 2.6. Honda monopodial branching tree models from L-systems.

n = 10
#define r1 0.9 /* коэффициент уменьшения длины ствола */
#define r2 0.6 /* коэффициент уменьшения длины веток */
#define a0 45 /* угол ветвления для ствола */
#define a2 45 /* угол ветвления для боковых сегментов */
#define d 137.5 /* угол расхождения */
#define wr 0.707 /* коэффициент уменьшения толщины */
ω : A(1,10)
p1: A(l,w) : *→ !(w)F(l)[&(a0)B(l*r2,w*wr)]/(d)A(l*r1,w*wr)
p2: B(l,w) : *→ !(w)F(l)[-(a2)$C(l*r2,w*wr)]C(l*r1,w*wr)
p3: C(l,w) : *→ !(w)F(l)[+(a2)$B(l*r2,w*wr)]B(l*r1,w*wr)
* This source code was highlighted with Source Code Highlighter.Table 2.1. Constants for monopodial wood structures in Figure 2.6.
Note per. - it is interesting here that the thickness of the segments between the tree nodes should be constant, and the picture shows that the trunk thickness begins to decrease even before the first branching, which contradicts the previous and subsequent arguments. In other pictures, this is not seen :)
According to the expression
 , at each iteration, a
, at each iteration, a 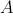 segment of the stem
segment of the stem 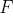 and a lateral vertex depart from the top of the main axis
and a lateral vertex depart from the top of the main axis 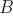 . The constants
. The constants 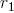 and
and 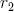 indicate the decrease in length for the straight and lateral segments,
indicate the decrease in length for the straight and lateral segments, 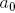 and
and 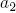 are the branch angles and
are the branch angles and 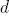 are the divergence angle. The module
are the divergence angle. The module 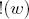 sets the line width
sets the line width  , so the expression
, so the expression  reduces the width of the child segments from the parent at
reduces the width of the child segments from the parent at  times. This constant satisfies the postulate of Leonardo da Vinci, according to which the total thickness of all branches folded together in any section of a tree with a horizontal plane is equal to the thickness of the trunk under them. In the event that
times. This constant satisfies the postulate of Leonardo da Vinci, according to which the total thickness of all branches folded together in any section of a tree with a horizontal plane is equal to the thickness of the trunk under them. In the event that 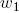 two daughter branches of equal diameter exit from the mother branch
two daughter branches of equal diameter exit from the mother branch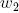 , this postulate gives the equation
, this postulate gives the equation 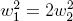 , therefore, the value
, therefore, the value 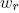 is equal
is equal 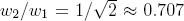 .
.Note trans. - by the thickness of the branches and the thickness of the trunk, one should probably understand their cross-sectional area, then it becomes clear where the squares appeared in the last equations.
Expressions
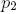 and
and 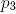 describe the further development of the side branches. At each iteration, a straight vertex (
describe the further development of the side branches. At each iteration, a straight vertex ( 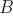 or
or  ) releases a lateral vertex of the next order at an angle
) releases a lateral vertex of the next order at an angle 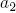 or
or 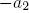 with respect to the mother axis. Both expressions are used to create lateral vertices alternately left and right. The symbol
with respect to the mother axis. Both expressions are used to create lateral vertices alternately left and right. The symbol 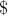 rotates the turtle around its own axis, and the vector
rotates the turtle around its own axis, and the vector 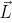 indicating the direction of the “left” turtle is drawn horizontally. Consequently, the branch plane is “closest to the horizontal plane”, as required by the Honda model. Writing in vector form,
indicating the direction of the “left” turtle is drawn horizontally. Consequently, the branch plane is “closest to the horizontal plane”, as required by the Honda model. Writing in vector form, 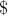 changes the orientation of the turtle in space according to:
changes the orientation of the turtle in space according to: 
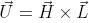
where are the vectors
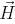 ,
, 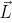 and
and - the main, left and top vectors attached to the turtle,
- the main, left and top vectors attached to the turtle, 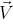 - a vector directed in the opposite direction from the direction of gravity. Figure 2.6 shows the trees that are modeled at the constants listed in Table 2.1 and match the Honda tree models.
- a vector directed in the opposite direction from the direction of gravity. Figure 2.6 shows the trees that are modeled at the constants listed in Table 2.1 and match the Honda tree models.Sympodial branching.
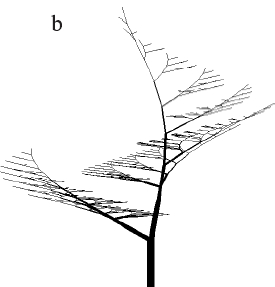
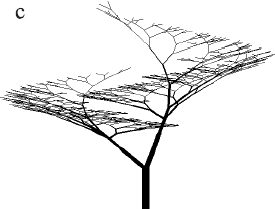
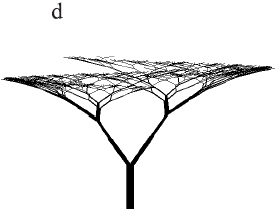
Other L-systems, shown in Figure 2.7, cover sympodial structures in which both daughter segments form a non-zero angle with the parent. In this case, the activity of the main peak is reduced due to the formation of the trunk
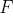 and a pair of lateral peaks
and a pair of lateral peaks 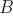 (expression
(expression  ). Further branching is done by expression
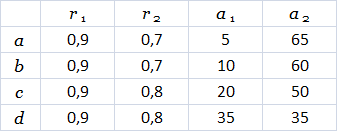
). Further branching is done by expression 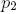 . The simple structures in Figure 2.7 were obtained using the constants listed in Table 2.2 and correspond to the models presented by Eono and Kuniai. Figure 2.7. Models of trees with sympodial branching Eono and Kuniay obtained on L-systems.
. The simple structures in Figure 2.7 were obtained using the constants listed in Table 2.2 and correspond to the models presented by Eono and Kuniai. Figure 2.7. Models of trees with sympodial branching Eono and Kuniay obtained on L-systems.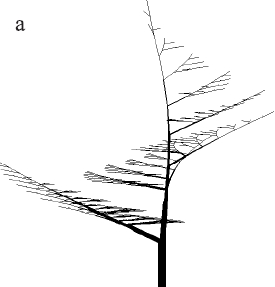
n = 10
#define r1 0.9 /* коэффициент уменьшения длины 1 */
#define r2 0.7 /* коэффициент уменьшения длины 2 */
#define a1 10 /* угол ветвления 1 */
#define a2 60 /* угол ветвления 2 */
#define wr 0.707 /* коэффициент уменьшения ширины */
ω : A(1,10)
p1 : A(l,w) : *→ !(w)F(l)[&(a1)B(l*r1,w*wr)]
/(180)[&(a2)B(l*r2,w*wr)]
p2 : B(l,w) : *→ !(w)F(l)[+(a1)$B(l*r1,w*wr)]
[-(a2)$B(l*r2,w*wr)]
* This source code was highlighted with Source Code Highlighter.Table 2.2 Constants for trees with sympodial branching in Figure 2.7.
Previous models have a somewhat artificial character, because the final length of each segment is set even when it is created, and does not change in further iterations. But it is possible to simulate the growth process itself, that is, to increase the length and width of the parent segments with the growth of subsidiaries. An example of an L-system constructed using this paradigm is given in Figure 2.8.
Ternary branching.
The general structure of the tree is defined by the expression
 . At each iteration, the vertex
. At each iteration, the vertex 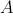 produces 3 new branches ending in their own vertices. The parameter
produces 3 new branches ending in their own vertices. The parameter  and constant
and constant 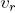 determine the ratio of the width of the parent branch
determine the ratio of the width of the parent branch 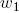 to the width of the child branch
to the width of the child branch 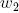 . According postulate da Vinci
. According postulate da Vinci  thereby
thereby  . Expression
. Expression 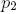 and
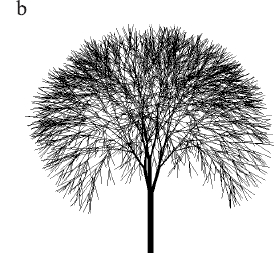
and 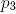 describe a gradual change in the length of the branches and increase in diameter. Figure 2.8. Models of trees with ternary branching.
describe a gradual change in the length of the branches and increase in diameter. Figure 2.8. Models of trees with ternary branching.


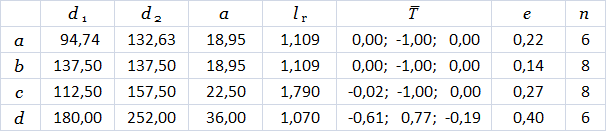
#define d1 94.74 /* угол расхождения 1 */
#define d2 132.63 /* угол расхождения 2 */
#define a 18.95 /* угол ветвления */
#define lr 1.109 /* коэффициент удлинения */
#define vr 1.732 /* коэффициент увеличения ширины */
ω : !(1)F(200)/(45)A
p1 : A : *→ !(vr)F(50)[&(a)F(50)A]/(d1)
[&(a)F(50)A]/(d2)[&(a)F(50)A]
p2 : F(l) : *→ F(l*lr)
p3 : !(w) : *→ !(w*vr)
* This source code was highlighted with Source Code Highlighter.Table 2.3. Constants for tree models in Figure 2.8.
Tropism is the reaction of an organism, for example a plant, to an external effect by growth in the direction determined by this effect. In particular, the desire of plants for light is manifested in the form of curving branches. This is modeled by a small rotation of the turtle after drawing each segment in the direction determined by the tropism vector
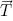 (Figure 2.9). The rotation angle a is calculated using the formula
(Figure 2.9). The rotation angle a is calculated using the formula 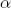 =
= 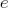 |
| 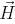
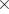
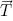 |, where
|, where 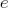 is the parameter characterizing the sensitivity, susceptibility of the axis to rotation. This formula has a physical explanation: if
is the parameter characterizing the sensitivity, susceptibility of the axis to rotation. This formula has a physical explanation: if 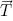 interpreted as the force applied to the end of the vector
interpreted as the force applied to the end of the vector 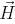 , and
, and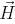 can rotate around its starting point, then the torque is equal
can rotate around its starting point, then the torque is equal 
 . The parameters related to the generation of tree models in Figure 2.8 are shown in Table 2.3. The realistic render of the tree in Figure 2.8d is shown in Figure 2.10.
. The parameters related to the generation of tree models in Figure 2.8 are shown in Table 2.3. The realistic render of the tree in Figure 2.8d is shown in Figure 2.10. 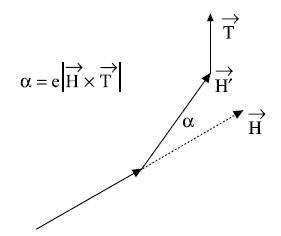
Figure 2.9. Correction of the
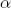 segment
segment 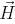 due to tropism
due to tropism 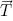 . Figure 2.10. The enchanting lake of Musgrave and others. Figure 2.11. Surreal lift.
. Figure 2.10. The enchanting lake of Musgrave and others. Figure 2.11. Surreal lift.

Conclusion
The examples given above show that Honda tree models, as well as models of his followers Eono and Kuniai can be obtained using L-systems. Shebell also showed that L-systems can play an important role as a tool for biologically correct tree modeling and synthesis of photorealistic images. However, while the obtained models are of a general nature, the structures of specific trees are still in development. L-systems are also widely used in the field of realistic modeling of grass plants, discussed in the next chapter.
PS If the "photorealistic" images from the 1990 book do not deliver, then perhaps more modern renderings from another article ( pdf ) on algorithmicbotany.org will seem interesting: PPS The translation does not provide an infinite number of references to the literature that is in the original book. The numbering of tables and pictures is left the original. The original book is here: algorithmicbotany.org/papers/#abop . If the site is down, you can download the book in pdf here: all , only the second chapter . If the text contains spelling / technical errors, please immediately inform in PM))


