Understanding particle physics: 1) ball-on-spring, Newtonian version
- Transfer
1. Ball on spring, Newtonian version
2. Quantum ball on spring
3. Waves, classic view
4. Waves, classical equation of motion
5. Quantum waves
6. Fields
7. Particles are quanta
8. How particles interact with fields
Understanding in general the fundamentals of particle physics - and this is our current understanding of most elementary phenomena of the Universe - is not so difficult. It will be easier for you if you have attended a physical and mathematical school or have gone through the first year of an institute. But if you deal with algebra, trigonometry and (perhaps, but not necessarily) with the basics of differentiation and integration, then you can understand how fields work and how particles appear. You only need to take my word for once about one aspect of quantum mechanics. In that case, I will not give mathematical formulas, but just show you the ready-made answers. But after you accept this aspect, everything else will be clear.
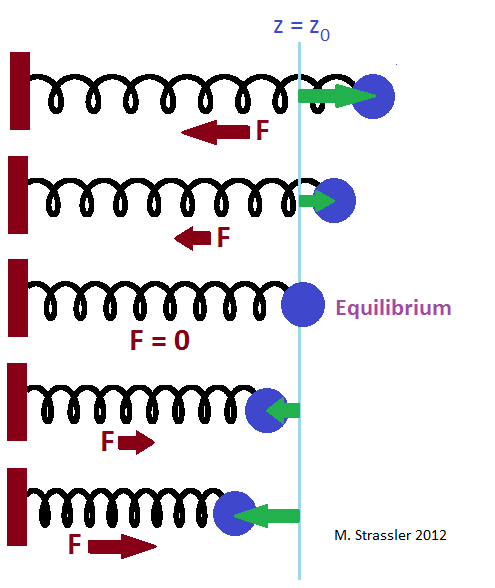
Fig. one
To understand particle physics, from school physics you need to remember one single thing - how the spring works. In fact, everything that jumps, vibrates, rings, rattles, swings back and forth, is an example of a spring.
Imagine that we placed a ball at the end of a spring. The motions of the spring and the equations describing it are simple. First, let's remember the basics of spring behavior, then we will study the ball's behavior - oscillation. And, finally, for the most inquisitive minds, we consider the equations leading to this kind of movement.
The ball on the spring has an equilibrium position; if you put a ball there and release it, the spring will not push it in either direction, and the ball will remain immovable. This is the blue line in fig. 1. If you pull the ball away from the equilibrium position (green arrows), the spring will pull the ball back with the force F (red arrows). The further you pull the ball, the stronger the spring will be to pull it back (at least until you tear the spring or break it with pressure).
We call the direction of the ball movement “direction z”, and define the z axis so that z = z 0 corresponds to the equilibrium position of the ball on the spring. Suppose we pull the ball from this position, hold it so that it does not move, to the position z = z 0 + A; then, at a certain point in time t = 0, we release it. The ball will start jumping to and fro - see fig. 2. The size of the jumps - the amplitude of the oscillations - is equal to A. It can be arbitrarily large or small; only you choose how to pull the ball from the equilibrium position. But how often jumps occur to and fro - the frequency of oscillations ν - you do not control. It turns out to be the same, regardless of the value of A. It is determined only by the properties of the ball and the spring, and not by what you are doing.
For scientific purposes, it is imperative to describe the observations through a mathematical formula. The position of the ball z is a function of time t, written by us as z (t), takes the form:
Where, as usual, cos is the cosine, π is the pi number from the geometry of the circle, z 0 is the equilibrium position of the ball, A and ν (nu) are the amplitude and frequency of oscillations. The cosine function is oscillatory; therefore, this formula describes oscillatory motions with amplitude A and frequency ν. Examples of the oscillatory motion of a ball on a spring with different values of the initial deflection and the final amplitude A are shown in fig. 2, which also shows that for a given ball on a spring, the frequency ν does not depend on the amplitude A.
Fine print: the amplitude and frequency are greater than zero. If A is negative, then the amplitude will be –A. In fact, the amplitude is actually | A |, that is, the magnitude of the magnitude.

Fig. 2
What is very important to remember about the amplitude and frequency of the ball and spring (in classical pre-quantum physics):
• amplitude A can be chosen any;
• The frequency ν is determined by the ball and the spring, and in order to choose a different frequency, you will have to replace the spring or ball.
The period of each oscillation (how long the ball needs to go forward and back exactly once) is called T, and this period is simply equal to the inverse of the frequency: T = 1 / ν. If the period is 5 seconds, then the frequency is once every five seconds, or 1/5 second (which is often called 1/5 Hertz or Hz).
Another fine print: in any real system of a spring and a ball, which you will encounter in everyday life, the friction will cause A to gradually decrease and eventually reach zero when the movement stops. Formulas that take into account the friction when moving, are not much more difficult, but we do not need them. Therefore, I always assume that friction is small, A is decreasing very slowly, and we can simply use simplified formulas that ignore friction. But it is important to know: friction reduces A, but, if it is not extremely strong, it does not affect ν and T! The oscillation frequency remains the same even with a decrease in amplitude. Therefore, the note that the guitar string gives out after you pull it does not change, even when the resulting sound gradually fades out.
One more thing: there is a beautiful formula for energy stored in an oscillating spring. It is proportional to the square of the amplitude and the square of the frequency:
This is partly the energy of motion of the ball (kinetic), and partly the interaction energy (potential) stored in the spring, and when the ball swings to and fro, the shares of these energies in the total energy constantly change. But the total energy E remains constant.
Small print: there is still energy of the mass of the ball, Mc 2 , but we do not keep track of it, because it is always there, the spring moves with it, or not.
The same vibrational formula applies to almost anything that trembles or jumps only if these jumps are not too large. A ball rolling around the bottom of the bowl; a car jumping on bad shock absorbers; vibrating string of a violin or guitar; xylophone bar after hitting it; etc.
Now let's remember the basic formulas explaining to us why the ball on the spring oscillates.
As we mentioned at the beginning (Fig. 1), the ball on the spring has an equilibrium position, which we called z = z 0 . Suppose at some point in time (either we pulled the ball, or it hesitated) it is in a different position, z. If z> z 0 , that is, if the offset from the equilibrium position z - z 0 is greater than zero, then the spring will create a force in the negative z direction to pull the ball back to the equilibrium point. Conversely, if z <z 0 , then there is a shift from equilibrium z - z 0negative, then the spring will create a force directed in the positive z direction, to pull the ball back to the equilibrium point. And the farther the ball is from the equilibrium position, the more the spring pulls. The force F, created by the spring, is associated with the displacement of the ball from the equilibrium by the equation
Where K is a positive value depending on a particular spring, called the spring constant.
Note why this formula is correct:
• If the ball is in the equilibrium position, F = 0. The spring does not create force, and if the ball does not move in the equilibrium position, it will remain there.
• If the deviation is greater than zero, the force is negative.
• If the deviation is negative, the force is positive.
• The greater the deviation, the greater the force.
Then we turn to Newton's second law of motion, which says that under the influence of force F, the ball of mass M will move with acceleration a, where F = M a. We substitute this into the formula and get
or
This is the equation we almost need, from which we can derive the oscillation equation. We only need to recall the relationship between a and z. For this, it is important to recall the relationship between a and the speed v, and between v and z. This ratio is one of two changes in time:
• Speed is the change in position over time, v = dz / dt
• Acceleration is the change in speed over time, a = dv / dt
Add and get
Acceleration is a change in time of a change in position over time.
We can rewrite our equation of motion
Where z is a brief entry for z (t). And now you can check that the oscillatory motion z (t) = z 0 + A cos [2 π ν t] will be the solution for this equation of motion. We need to first calculate the speed of the particle as a change in its position in time:
(dz 0 / dt = 0, because the equilibrium position z 0 does not change with time, and d / dt (cos wt) = -w sin wt); and then we calculate the particle acceleration as a change in its velocity over time:
(since d / dt (sin wt) = w cos wt). As a result
Where in the last step I used the formula z (t) = z 0 + A cos [2 π ν t] for the oscillatory motion. The resulting equation is the same as our equation of motion [ ], given that (2 π ν) 2 = K / M, if the oscillation frequency is
], given that (2 π ν) 2 = K / M, if the oscillation frequency is
And we, in fact, found that our equation of motion implies that the spring will oscillate with the indicated frequency, that this frequency does not depend on A - it depends only on the properties of the spring (K) and the ball (M) - and that from the value of A for the equation there is a solution. Therefore, we can choose any A, depending on how far we delay the ball from its equilibrium position before releasing it.
Resonance is one of the most important natural phenomena, both in ordinary life, where it plays a role in many aspects of technology and in music, and in the basic processes of the physical world, especially in particle physics.
First, remember how the swing works. A swing, like a spring ball, or any pendulum, is an oscillator — it swings back and forth with a certain frequency that does not depend on the swing amplitude. In the case of a swing, this statement remains true as long as the amplitude is not very large. Probably from experience you know that in order to swing a child higher, you need to push the swing forward once per cycle so that the swing amplitude constantly increases. If you push the swing forward several times in a cycle, or once every two and a half cycles, sometimes you will increase the swing amplitude and sometimes decrease it. Obviously, there is something special about equalizing the frequency with which you are pushing the swing, with the natural frequency of the swing itself.
Similarly, if the child himself knows how to rock the swing, he knows that he needs to swing his legs at the same time as the natural frequency of the swing in order to increase the amplitude of the swing. Swing the other way, and the amplitude will not grow.
You can trace how this happens with the ball on the spring. Look at the drawing. On the left, a ball is shown, oscillating to and fro around an equilibrium position. He hesitates himself, without external shocks. It oscillates with the natural frequency of the spring ν. The frequency is √ K / M, where K is the spring force, M is the mass of the ball.
Right on fig. You can see what happens to the other black ball, the mass of which is equal to the first one, on the same spring that is pushed with a force F (its magnitude and direction are indicated by a red arrow), which oscillates at a frequency ν Fdifferent from ν. The black ball behaves just like a swing, which is too rarely pushed; they will move according to a complex pattern and will not climb high. In fig. it can be seen that the ball does not oscillate very smoothly, and the amplitude of oscillations is small. You can see how he is "trying" to oscillate with a natural frequency, although its overall movement is repeated at a frequency v the F .
Then the figure shows a case in which the force oscillates with a frequency ν F much higher than the frequency ν. Again, you can see how he “tries” to oscillate with a natural frequency, but he cannot do it with a large amplitude, because the rapidly oscillating force can both push him both along and against the motion, then increasing, then decreasing the amplitude .
And at the end is shown the case when the force oscillates with the natural frequency of the spring, ν F = ν. The ball reacts quite differently: the amplitude of the oscillations is constantly increasing, and the black ball oscillates as easily and smoothly as the white ball on the left, but with increasing amplitude. This is a resonance.
The result: if ν F differs from ν - if the force does not give the ball a resonance - it will move, but reluctantly, and its movement will be very different from the natural, from a simple oscillation with frequency ν. On the contrary, if the frequency of the force corresponds to the natural one — if the force introduces the ball into resonance, then the force pushes the ball much more efficiently, and the resulting movement is more impressive. We know this intuitively; pushing the swing with a natural frequency, the child (or parent) swinging the swing higher and higher.
Among the important aspects of resonance in particle physics is the fact that in certain circumstances particles can be generated due to a very similar mechanism: after a collision of two particles, a force is obtained with exactly the frequency that is required to create a third one.
This is the behavior of a ball on a spring in classical, pre-quantum, physics. Quantum mechanics changes many concepts , but the most important thing is this: we can still choose A, but A cannot be any value. It can only take certain values that are proportional to the square root of integers.
2. Quantum ball on spring
3. Waves, classic view
4. Waves, classical equation of motion
5. Quantum waves
6. Fields
7. Particles are quanta
8. How particles interact with fields
Understanding in general the fundamentals of particle physics - and this is our current understanding of most elementary phenomena of the Universe - is not so difficult. It will be easier for you if you have attended a physical and mathematical school or have gone through the first year of an institute. But if you deal with algebra, trigonometry and (perhaps, but not necessarily) with the basics of differentiation and integration, then you can understand how fields work and how particles appear. You only need to take my word for once about one aspect of quantum mechanics. In that case, I will not give mathematical formulas, but just show you the ready-made answers. But after you accept this aspect, everything else will be clear.

Fig. one
To understand particle physics, from school physics you need to remember one single thing - how the spring works. In fact, everything that jumps, vibrates, rings, rattles, swings back and forth, is an example of a spring.
Imagine that we placed a ball at the end of a spring. The motions of the spring and the equations describing it are simple. First, let's remember the basics of spring behavior, then we will study the ball's behavior - oscillation. And, finally, for the most inquisitive minds, we consider the equations leading to this kind of movement.
Harmonic oscillator (aka - a ball on a spring)
The ball on the spring has an equilibrium position; if you put a ball there and release it, the spring will not push it in either direction, and the ball will remain immovable. This is the blue line in fig. 1. If you pull the ball away from the equilibrium position (green arrows), the spring will pull the ball back with the force F (red arrows). The further you pull the ball, the stronger the spring will be to pull it back (at least until you tear the spring or break it with pressure).
Oscillatory movement (jumping)
We call the direction of the ball movement “direction z”, and define the z axis so that z = z 0 corresponds to the equilibrium position of the ball on the spring. Suppose we pull the ball from this position, hold it so that it does not move, to the position z = z 0 + A; then, at a certain point in time t = 0, we release it. The ball will start jumping to and fro - see fig. 2. The size of the jumps - the amplitude of the oscillations - is equal to A. It can be arbitrarily large or small; only you choose how to pull the ball from the equilibrium position. But how often jumps occur to and fro - the frequency of oscillations ν - you do not control. It turns out to be the same, regardless of the value of A. It is determined only by the properties of the ball and the spring, and not by what you are doing.
For scientific purposes, it is imperative to describe the observations through a mathematical formula. The position of the ball z is a function of time t, written by us as z (t), takes the form:
Where, as usual, cos is the cosine, π is the pi number from the geometry of the circle, z 0 is the equilibrium position of the ball, A and ν (nu) are the amplitude and frequency of oscillations. The cosine function is oscillatory; therefore, this formula describes oscillatory motions with amplitude A and frequency ν. Examples of the oscillatory motion of a ball on a spring with different values of the initial deflection and the final amplitude A are shown in fig. 2, which also shows that for a given ball on a spring, the frequency ν does not depend on the amplitude A.
Fine print: the amplitude and frequency are greater than zero. If A is negative, then the amplitude will be –A. In fact, the amplitude is actually | A |, that is, the magnitude of the magnitude.

Fig. 2
What is very important to remember about the amplitude and frequency of the ball and spring (in classical pre-quantum physics):
• amplitude A can be chosen any;
• The frequency ν is determined by the ball and the spring, and in order to choose a different frequency, you will have to replace the spring or ball.
The period of each oscillation (how long the ball needs to go forward and back exactly once) is called T, and this period is simply equal to the inverse of the frequency: T = 1 / ν. If the period is 5 seconds, then the frequency is once every five seconds, or 1/5 second (which is often called 1/5 Hertz or Hz).
Another fine print: in any real system of a spring and a ball, which you will encounter in everyday life, the friction will cause A to gradually decrease and eventually reach zero when the movement stops. Formulas that take into account the friction when moving, are not much more difficult, but we do not need them. Therefore, I always assume that friction is small, A is decreasing very slowly, and we can simply use simplified formulas that ignore friction. But it is important to know: friction reduces A, but, if it is not extremely strong, it does not affect ν and T! The oscillation frequency remains the same even with a decrease in amplitude. Therefore, the note that the guitar string gives out after you pull it does not change, even when the resulting sound gradually fades out.
One more thing: there is a beautiful formula for energy stored in an oscillating spring. It is proportional to the square of the amplitude and the square of the frequency:
This is partly the energy of motion of the ball (kinetic), and partly the interaction energy (potential) stored in the spring, and when the ball swings to and fro, the shares of these energies in the total energy constantly change. But the total energy E remains constant.
Small print: there is still energy of the mass of the ball, Mc 2 , but we do not keep track of it, because it is always there, the spring moves with it, or not.
The same vibrational formula applies to almost anything that trembles or jumps only if these jumps are not too large. A ball rolling around the bottom of the bowl; a car jumping on bad shock absorbers; vibrating string of a violin or guitar; xylophone bar after hitting it; etc.
Oscillatory motion equation (jump math)
Now let's remember the basic formulas explaining to us why the ball on the spring oscillates.
As we mentioned at the beginning (Fig. 1), the ball on the spring has an equilibrium position, which we called z = z 0 . Suppose at some point in time (either we pulled the ball, or it hesitated) it is in a different position, z. If z> z 0 , that is, if the offset from the equilibrium position z - z 0 is greater than zero, then the spring will create a force in the negative z direction to pull the ball back to the equilibrium point. Conversely, if z <z 0 , then there is a shift from equilibrium z - z 0negative, then the spring will create a force directed in the positive z direction, to pull the ball back to the equilibrium point. And the farther the ball is from the equilibrium position, the more the spring pulls. The force F, created by the spring, is associated with the displacement of the ball from the equilibrium by the equation
Where K is a positive value depending on a particular spring, called the spring constant.
Note why this formula is correct:
• If the ball is in the equilibrium position, F = 0. The spring does not create force, and if the ball does not move in the equilibrium position, it will remain there.
• If the deviation is greater than zero, the force is negative.
• If the deviation is negative, the force is positive.
• The greater the deviation, the greater the force.
Then we turn to Newton's second law of motion, which says that under the influence of force F, the ball of mass M will move with acceleration a, where F = M a. We substitute this into the formula and get
or
This is the equation we almost need, from which we can derive the oscillation equation. We only need to recall the relationship between a and z. For this, it is important to recall the relationship between a and the speed v, and between v and z. This ratio is one of two changes in time:
• Speed is the change in position over time, v = dz / dt
• Acceleration is the change in speed over time, a = dv / dt
Add and get
Acceleration is a change in time of a change in position over time.
We can rewrite our equation of motion
Where z is a brief entry for z (t). And now you can check that the oscillatory motion z (t) = z 0 + A cos [2 π ν t] will be the solution for this equation of motion. We need to first calculate the speed of the particle as a change in its position in time:
(dz 0 / dt = 0, because the equilibrium position z 0 does not change with time, and d / dt (cos wt) = -w sin wt); and then we calculate the particle acceleration as a change in its velocity over time:
(since d / dt (sin wt) = w cos wt). As a result
Where in the last step I used the formula z (t) = z 0 + A cos [2 π ν t] for the oscillatory motion. The resulting equation is the same as our equation of motion [
And we, in fact, found that our equation of motion implies that the spring will oscillate with the indicated frequency, that this frequency does not depend on A - it depends only on the properties of the spring (K) and the ball (M) - and that from the value of A for the equation there is a solution. Therefore, we can choose any A, depending on how far we delay the ball from its equilibrium position before releasing it.
Resonance
Resonance is one of the most important natural phenomena, both in ordinary life, where it plays a role in many aspects of technology and in music, and in the basic processes of the physical world, especially in particle physics.
First, remember how the swing works. A swing, like a spring ball, or any pendulum, is an oscillator — it swings back and forth with a certain frequency that does not depend on the swing amplitude. In the case of a swing, this statement remains true as long as the amplitude is not very large. Probably from experience you know that in order to swing a child higher, you need to push the swing forward once per cycle so that the swing amplitude constantly increases. If you push the swing forward several times in a cycle, or once every two and a half cycles, sometimes you will increase the swing amplitude and sometimes decrease it. Obviously, there is something special about equalizing the frequency with which you are pushing the swing, with the natural frequency of the swing itself.
Similarly, if the child himself knows how to rock the swing, he knows that he needs to swing his legs at the same time as the natural frequency of the swing in order to increase the amplitude of the swing. Swing the other way, and the amplitude will not grow.

You can trace how this happens with the ball on the spring. Look at the drawing. On the left, a ball is shown, oscillating to and fro around an equilibrium position. He hesitates himself, without external shocks. It oscillates with the natural frequency of the spring ν. The frequency is √ K / M, where K is the spring force, M is the mass of the ball.
Right on fig. You can see what happens to the other black ball, the mass of which is equal to the first one, on the same spring that is pushed with a force F (its magnitude and direction are indicated by a red arrow), which oscillates at a frequency ν Fdifferent from ν. The black ball behaves just like a swing, which is too rarely pushed; they will move according to a complex pattern and will not climb high. In fig. it can be seen that the ball does not oscillate very smoothly, and the amplitude of oscillations is small. You can see how he is "trying" to oscillate with a natural frequency, although its overall movement is repeated at a frequency v the F .
Then the figure shows a case in which the force oscillates with a frequency ν F much higher than the frequency ν. Again, you can see how he “tries” to oscillate with a natural frequency, but he cannot do it with a large amplitude, because the rapidly oscillating force can both push him both along and against the motion, then increasing, then decreasing the amplitude .
And at the end is shown the case when the force oscillates with the natural frequency of the spring, ν F = ν. The ball reacts quite differently: the amplitude of the oscillations is constantly increasing, and the black ball oscillates as easily and smoothly as the white ball on the left, but with increasing amplitude. This is a resonance.
The result: if ν F differs from ν - if the force does not give the ball a resonance - it will move, but reluctantly, and its movement will be very different from the natural, from a simple oscillation with frequency ν. On the contrary, if the frequency of the force corresponds to the natural one — if the force introduces the ball into resonance, then the force pushes the ball much more efficiently, and the resulting movement is more impressive. We know this intuitively; pushing the swing with a natural frequency, the child (or parent) swinging the swing higher and higher.
Among the important aspects of resonance in particle physics is the fact that in certain circumstances particles can be generated due to a very similar mechanism: after a collision of two particles, a force is obtained with exactly the frequency that is required to create a third one.
Next time: a quantum ball on a spring
This is the behavior of a ball on a spring in classical, pre-quantum, physics. Quantum mechanics changes many concepts , but the most important thing is this: we can still choose A, but A cannot be any value. It can only take certain values that are proportional to the square root of integers.
