Plasma Cash blockchain state data structures
- Tutorial
Hello, dear Habrausers! This article is about web 3.0, the Internet with decentralization. Web 3.0 introduces the concept of decentralization as the basis for the modern Internet; many computer systems and networks need security and decentralization properties for their needs. The decentralization solution is called distributed registry technology or blockchain.

Blockchain is a distributed registry. It can be considered as a huge database that lives forever and does not change in history, the blockchain is used as a basis for decentralized web applications or services.
In essence, blockchain is not only a database, it is an opportunity to increase trust between network participants with the ability to execute business logic on the network.
Byzantine consensus increases network reliability solves the challenge of consistency The
scalability that DLT brings is changing existing business networks.
Blockchain offers new very important advantages:
Opporty PoE is a project whose goal is to study cryptographic protocols and improve existing DLT and blockchain solutions.
Most public distributed registry systems do not have scalability properties — their throughput is rather low. For example, ethereum processes only ~ 20 tx / s.
Many solutions were created to increase the scalability property and not to lose decentralization (as you know, only 2 out of 3 can be known: scalability, security, decentralization).
One of the most effective is a solution using sidechains.
The concept is that the root chain processes a small number of commits from child chains, so that the root chain acts as the most secure and final layer for storing all intermediate states. Each child chain functions as its own blockchain with its own consensus algorithm, but there are some important caveats.
Validators have economic incentives to act honestly, and send comments to the root chain - the layer of the final settlement of the transaction.
As a result, dapp users working in child-chain should not interact with root-chain at all. In addition, they can withdraw their money to the root chain whenever they want, even if the child chain is hacked. These exits from the child-chain allow users to safely store their funds using Merkle proofs, confirming ownership of a certain amount of funds.
The main advantages of Plasma are related to its ability to significantly facilitate the calculations that currently overload the main chain. In addition, the Ethereum blockchain can process more extensive and more parallel datasets. Time taken from the root chain is also transferred to Ethereum nodes, which receive lower processing and storage requirements.
Plasma Cash is a design that gives network tokens unique serial numbers that turn them into unique tokens. Advantages of this include the absence of the need for confirmations, simpler support for all types of tokens (including Non-fungible tokens), and mitigation against mass exits from the child chain.
The plasma problem is related to the concept of "mass exits" from the child chain. In this scenario, a coordinated simultaneous exit from the daughter chain could potentially lead to a lack of computing power to withdraw all funds. As a result, users may lose money.

Base plasma has many options for implementation.
The main differences are:
The main variations of Plasma:
The purpose of this article is to explain the data structures that are used in the Plasma Cash blockchain.
In order to understand exactly how commitment works, you need to clarify the concept of the Merkle tree.
Merkle trees are an extremely important data structure in the blockchain world. In essence, Merkle trees give us the ability to capture some data set in a way that hides the data, but allows users to prove that some of the information was in the set. For example, if I have ten numbers, I can create proof for these numbers and then prove that one particular number was in this set of numbers. These proofs have a small constant size, which makes them cheap to publish to Ethereum.
You can use this for a set of transactions. You can also prove that a particular transaction is in this set of transactions. This is exactly what the operator does. Each block consists of a set of transactions that turn into a Merkle tree. The root of this tree is the proof, which is published in Ethereum along with each block of plasma.
Users should be able to withdraw their funds from the plasma chain. When users want to exit the plasma chain, they send the “exit” transaction to Ethereum.
Plasma Cash use special Merkle Tree which makes it possible not to validate the entire block but to validate only those branches that correspond to the user's token.
That is, to transfer a token, you need to go through the history and scan only those tokens that a certain user needs, when transferring a token, the user simply passes the entire history to another user and he can already authenticate the whole story - and most importantly, do it very quickly.

Nevertheless, it is necessary to use only some Merkle trees, because it is necessary to obtain proof of inclusion and also proof of non-inclusion of the transaction in the block, for example -
Opporty has implemented its Sparse Merkle Tree and Patricia Trie implementations. A
sparse Merkle tree is similar to a standard Merkle tree, except that the data contained in it is indexed and each data point is placed on a sheet that corresponds to the index of this data point.
Let's say we have a tree Merkla with four leaves. We will fill this tree with a few letters (A, D) for demonstration. The letter A is the first letter of the alphabet, so we must put it on the first sheet. Similarly, we can put D on the fourth sheet.
So what happens in the second and third leaves? We just leave them empty. More precisely, a special value (for example, zero) is placed instead of placing the letter.
The tree ultimately looks like this:

The proof of inclusion works just like in a regular Merkle tree. What happens if we want to prove that C is not part of this Merkle tree? It's simple! We know that if C were part of a tree, it would be on the third sheet. If C is not part of the tree, then the third leaf must be zero.
All that is needed is the standard proof of the inclusion of Merkle, showing that the third sheet is zero.
The best part of a sparse Merkle tree is that they really represent key-value stores inside the Merkle tree!
Here is part of the PoE protocol code that implements the Sparse Merkle Tree build.
This code is pretty trivial. We have a key-value store with proof of inclusion / non-inclusion.
In each iteration, a specific level of the final tree is filled, starting with the last one. Depending on which key of the current sheet is even or odd, we take two adjacent sheets and consider the hash of the current level. If we reach the end we write a single merkleRoot - a common hash.
You must understand that this tree is already filled with initially empty values! And if we store a huge amount of IDS token. we have a huge tree size and it takes a very long time to generate!
There are many solutions to this unoptimization, but Opporty decided to change this tree to Patricia Trie.
Patricia Trie is a mix of Radix Trie and Merkle Trie.
Radix Trie data key will store the data path itself! This allows you to create an optimized data structure for memory!
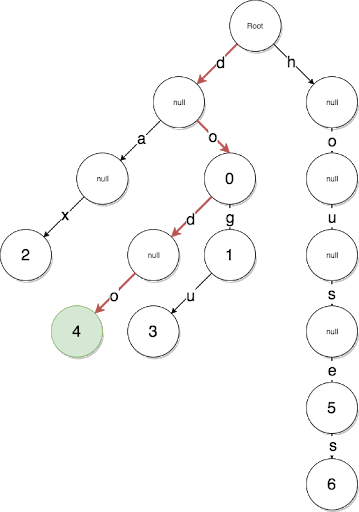
That is, we go through recursively and build separately left and right child subtrees. At the same time, building the key is like a path in this tree!
This solution is even more trivial and works faster while being quite optimized! In fact, Patricia tree can be further optimized by introducing new types of nodes - extension node, branch node, etc., as done in the ethereum protocol, but this implementation satisfies all our conditions - we got a fast and memory-optimized data structure.
By implementing these data structures, Opporty made it possible to scale Plasma Cash since it makes it possible to check the history of the token and the inclusion of not including the token in the tree! This allows you to greatly accelerate the validation of blocks and the Plasma Child Chain itself.

Blockchain is a distributed registry. It can be considered as a huge database that lives forever and does not change in history, the blockchain is used as a basis for decentralized web applications or services.
In essence, blockchain is not only a database, it is an opportunity to increase trust between network participants with the ability to execute business logic on the network.
Byzantine consensus increases network reliability solves the challenge of consistency The
scalability that DLT brings is changing existing business networks.
Blockchain offers new very important advantages:
- Prevention of costly mistakes.
- Transparent transactions.
- Digitization for real goods.
- Smart contracts.
- Speed and security of payments.
Opporty PoE is a project whose goal is to study cryptographic protocols and improve existing DLT and blockchain solutions.
Most public distributed registry systems do not have scalability properties — their throughput is rather low. For example, ethereum processes only ~ 20 tx / s.
Many solutions were created to increase the scalability property and not to lose decentralization (as you know, only 2 out of 3 can be known: scalability, security, decentralization).
One of the most effective is a solution using sidechains.
Plasma concept
The concept is that the root chain processes a small number of commits from child chains, so that the root chain acts as the most secure and final layer for storing all intermediate states. Each child chain functions as its own blockchain with its own consensus algorithm, but there are some important caveats.
- Smart contracts are created in the root chain and act as a checkpoint on the child chain in the root chain.
- A child chain is created that functions as its own blockchain with its own consensus. All states in the chain of child processes are protected by fraud proofs, which ensure that all transitions between states are valid and apply a withdrawal protocol.
- Smart contracts specific to dapp or child-chain (application logic) can then be deployed to child chain.
- The necessary tools can be transferred from root-chain to child-chain.
Validators have economic incentives to act honestly, and send comments to the root chain - the layer of the final settlement of the transaction.
As a result, dapp users working in child-chain should not interact with root-chain at all. In addition, they can withdraw their money to the root chain whenever they want, even if the child chain is hacked. These exits from the child-chain allow users to safely store their funds using Merkle proofs, confirming ownership of a certain amount of funds.
The main advantages of Plasma are related to its ability to significantly facilitate the calculations that currently overload the main chain. In addition, the Ethereum blockchain can process more extensive and more parallel datasets. Time taken from the root chain is also transferred to Ethereum nodes, which receive lower processing and storage requirements.
Plasma Cash is a design that gives network tokens unique serial numbers that turn them into unique tokens. Advantages of this include the absence of the need for confirmations, simpler support for all types of tokens (including Non-fungible tokens), and mitigation against mass exits from the child chain.
The plasma problem is related to the concept of "mass exits" from the child chain. In this scenario, a coordinated simultaneous exit from the daughter chain could potentially lead to a lack of computing power to withdraw all funds. As a result, users may lose money.
Plasma Implementation Options

Base plasma has many options for implementation.
The main differences are:
- storing information about the method of storing and presenting the state,
- types of tokens (divisible indivisible),
- transaction security
- type of consensus algorithm, etc.
The main variations of Plasma:
- UTXO based - each transaction consists of inputs and outputs: a transaction can be conducted and spent, the list of transactions not spent is a state of the child-chain itself.
- Account based - simply contains a reflection of each account-account and its balance, this type is used in ethereum since each account can be of two types - a user account and a smart contract account. The advantage of this type of state storage is its simplicity, and the minus is that this option is not scalable (the special nonce property is used to prevent the transaction from being executed twice).
The purpose of this article is to explain the data structures that are used in the Plasma Cash blockchain.
In order to understand exactly how commitment works, you need to clarify the concept of the Merkle tree.
Merkle trees their use in Plasma
Merkle trees are an extremely important data structure in the blockchain world. In essence, Merkle trees give us the ability to capture some data set in a way that hides the data, but allows users to prove that some of the information was in the set. For example, if I have ten numbers, I can create proof for these numbers and then prove that one particular number was in this set of numbers. These proofs have a small constant size, which makes them cheap to publish to Ethereum.
You can use this for a set of transactions. You can also prove that a particular transaction is in this set of transactions. This is exactly what the operator does. Each block consists of a set of transactions that turn into a Merkle tree. The root of this tree is the proof, which is published in Ethereum along with each block of plasma.
Users should be able to withdraw their funds from the plasma chain. When users want to exit the plasma chain, they send the “exit” transaction to Ethereum.
Plasma Cash use special Merkle Tree which makes it possible not to validate the entire block but to validate only those branches that correspond to the user's token.
That is, to transfer a token, you need to go through the history and scan only those tokens that a certain user needs, when transferring a token, the user simply passes the entire history to another user and he can already authenticate the whole story - and most importantly, do it very quickly.

Plasma Cash data structures for storing status and history
Nevertheless, it is necessary to use only some Merkle trees, because it is necessary to obtain proof of inclusion and also proof of non-inclusion of the transaction in the block, for example -
- Sparse merkle tree
- Patricia trie
Opporty has implemented its Sparse Merkle Tree and Patricia Trie implementations. A
sparse Merkle tree is similar to a standard Merkle tree, except that the data contained in it is indexed and each data point is placed on a sheet that corresponds to the index of this data point.
Let's say we have a tree Merkla with four leaves. We will fill this tree with a few letters (A, D) for demonstration. The letter A is the first letter of the alphabet, so we must put it on the first sheet. Similarly, we can put D on the fourth sheet.
So what happens in the second and third leaves? We just leave them empty. More precisely, a special value (for example, zero) is placed instead of placing the letter.
The tree ultimately looks like this:

The proof of inclusion works just like in a regular Merkle tree. What happens if we want to prove that C is not part of this Merkle tree? It's simple! We know that if C were part of a tree, it would be on the third sheet. If C is not part of the tree, then the third leaf must be zero.
All that is needed is the standard proof of the inclusion of Merkle, showing that the third sheet is zero.
The best part of a sparse Merkle tree is that they really represent key-value stores inside the Merkle tree!
Here is part of the PoE protocol code that implements the Sparse Merkle Tree build.
class SparseTree {
//...
buildTree() {
if (Object.keys(this.leaves).length > 0) {
this.levels = []
this.levels.unshift(this.leaves)
for (let level = 0; level < this.depth; level++) {
let currentLevel = this.levels[0]
let nextLevel = {}
Object.keys(currentLevel).forEach((leafKey) => {
let leafHash = currentLevel[leafKey]
let isEvenLeaf = this.isEvenLeaf(leafKey)
let parentLeafKey = leafKey.slice(0, -1)
let neighborLeafKey = parentLeafKey + (isEvenLeaf ? '1' : '0')
let neighborLeafHash = currentLevel[neighborLeafKey]
if (!neighborLeafHash) {
neighborLeafHash = this.defaultHashes[level]
}
if (!nextLevel[parentLeafKey]) {
let parentLeafHash = isEvenLeaf ?
ethUtil.sha3(Buffer.concat([leafHash, neighborLeafHash])) :
ethUtil.sha3(Buffer.concat([neighborLeafHash, leafHash]))
if (level == this.depth - 1) {
nextLevel['merkleRoot'] = parentLeafHash
} else {
nextLevel[parentLeafKey] = parentLeafHash
}
}
})
this.levels.unshift(nextLevel)
}
}
}
}This code is pretty trivial. We have a key-value store with proof of inclusion / non-inclusion.
In each iteration, a specific level of the final tree is filled, starting with the last one. Depending on which key of the current sheet is even or odd, we take two adjacent sheets and consider the hash of the current level. If we reach the end we write a single merkleRoot - a common hash.
You must understand that this tree is already filled with initially empty values! And if we store a huge amount of IDS token. we have a huge tree size and it takes a very long time to generate!
There are many solutions to this unoptimization, but Opporty decided to change this tree to Patricia Trie.
Patricia Trie is a mix of Radix Trie and Merkle Trie.
Radix Trie data key will store the data path itself! This allows you to create an optimized data structure for memory!

Opporty implementation
buildNode(childNodes, key = '', level = 0) {
let node = {key}
this.iterations++
if (childNodes.length == 1) {
let nodeKey = level == 0 ?
childNodes[0].key :
childNodes[0].key.slice(level - 1)
node.key = nodeKey
let nodeHashes = Buffer.concat([Buffer.from(ethUtil.sha3(nodeKey)),
childNodes[0].hash])
node.hash = ethUtil.sha3(nodeHashes)
return node
}
let leftChilds = []
let rightChilds = []
childNodes.forEach((node) => {
if (node.key[level] == '1') {
rightChilds.push(node)
} else {
leftChilds.push(node)
}
})
if (leftChilds.length && rightChilds.length) {
node.leftChild = this.buildNode(leftChilds, '0', level + 1)
node.rightChild = this.buildNode(rightChilds, '1', level + 1)
let nodeHashes = Buffer.concat([Buffer.from(ethUtil.sha3(node.key)),
node.leftChild.hash,
node.rightChild.hash])
node.hash = ethUtil.sha3(nodeHashes)
} else if (leftChilds.length && !rightChilds.length) {
node = this.buildNode(leftChilds, key + '0', level + 1)
} else if (!leftChilds.length && rightChilds.length) {
node = this.buildNode(rightChilds, key + '1', level + 1)
} else if (!leftChilds.length && !rightChilds.length) {
throw new Error('invalid tree')
}
return node
}
That is, we go through recursively and build separately left and right child subtrees. At the same time, building the key is like a path in this tree!
This solution is even more trivial and works faster while being quite optimized! In fact, Patricia tree can be further optimized by introducing new types of nodes - extension node, branch node, etc., as done in the ethereum protocol, but this implementation satisfies all our conditions - we got a fast and memory-optimized data structure.
By implementing these data structures, Opporty made it possible to scale Plasma Cash since it makes it possible to check the history of the token and the inclusion of not including the token in the tree! This allows you to greatly accelerate the validation of blocks and the Plasma Child Chain itself.
