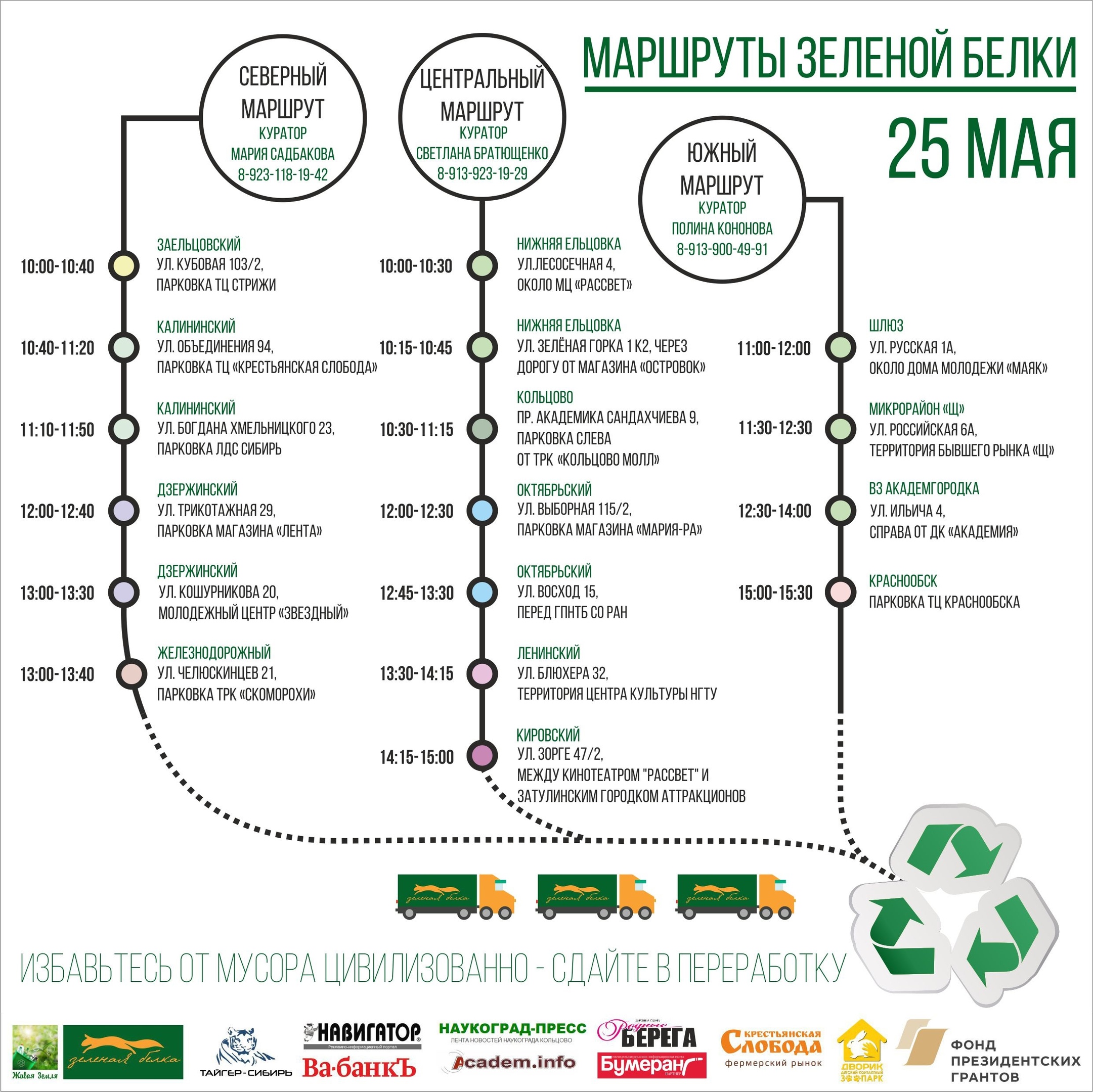
Logistics of the action for separate collection of recyclables

Instead of joining

When the processes of waste collection and processing are fully adjusted in Russia, it is not easy to say, but I want to not participate in the replenishment of landfills now. Therefore, in many large cities, one way or another, there are volunteer movements engaged in particular separate collection.

In Novosibirsk, such an activity is formed around the Green Squirrel campaign, in which once a month environmental townspeople bring accumulated recyclable household waste to predetermined places at a certain time. By the same time, a rented truck arrives there, which takes the collected and sorted recyclable materials to the site, from where it is redistributed between various processing enterprises. The action has existed since 2014, and since then the number of collection points for recyclables, as well as its volumes, has significantly increased. For truck routing, just a gaze was not enough, and we began to develop optimization models to minimize transportation costs. The first of these models is the subject of this article.

In section 1, I will describe in detail and with illustrations the scheme for organizing the action. Further, in Section 2, the task of minimizing transport costs will be formalized as the task of routing heterogeneous vehicles fleet vehicle routing problem with time windows. Section 3 is devoted to solving this problem using a freely distributed package for solving mixed integer linear mathematical programming problems GLPK.

1. The action "Green Squirrel"

Since 2014, the Living Earth initiative group has been conducting a monthly campaign to separate the collection of recycled Green Squirrel in Novosibirsk. At the time of writing, recycling with a number of reservations is accepted plastic waste labeled PET, PE, PP, PS, glass, aluminum, iron, household appliances, waste paper and more. More than 50 volunteers participate in the preparation and conduct of the action. The action is not commercial, participation in it is free and does not imply a monetary reward.

Points

The action is held at 17 points of the city, located from each other at distances covered by the car in a period of 15 to 90 minutes. One of these points in the photo: bags on the left along the wall to collect various fractions of plastic, on the right - a truck, in which everything is loaded in the future, and in the center - a volunteer with ears.



All activity at the point is organized by curators who have restrictions on the time at which they are ready to fulfill their duties. When planning an action, curators report the time interval within which the action must pass at their point.

There is also data on the average volumes of recyclables collected at each point.

Routes

Points are organized into routes that are successively driven by a truck. Truck movements are monitored by route supervisors who monitor the operational environment and make decisions on handling special events.



Trucks

Are rented on a common basis within the framework of proposals for hourly rental of freight vehicles. It is not possible to compact the plastic in place, therefore the main parameter characterizing the truck is the volume of the body. Carrying capacity in our case is not a limiting factor.

The main expenses of the action are connected with the payment of truck rental, therefore, its reduction is critical for the existence and development of our share, which acquires institutional significance in the sense of forming ideas about responsible consumption. Next, an approach to solving this issue will be described, based on the application of discrete optimization methods, namely, mathematical programming.

2. Formalization

In constructing the mathematical model, we will remain within the framework of linear mixed-integer programs, for which understanding knowledge of class 7 algebra is sufficient.

The only difficulty can be associated with the use of abstract notation and summation signs in formulas. I hope this does not scare away readers who have infrequent encounters with mathematical texts.

In the optimization model, four components can be distinguished:

• the formation of groups of points that make up a separate route;
• definition of a detour scheme for each of the groups;
• meeting the requirements for the time of arrival of the truck at each point;
• determination of the type of truck needed to service each of the routes.

We consider each of the parts, introducing the necessary notation as necessary.

The formation of groups of points

Let$$there are many indexes of collection points for recyclable materials, and the site where collected recyclables are then transported - we will call it a depot - has an index of 0. Put$$

Each group of points forms a separate route. Through$$denote the set of route numbers.

Let the quantity$$ equals one if the point $$ included in the route with the number $$, and zero otherwise. Then the requirement that the point$$ must enter one of the routes can be written as

$$

Depot must enter all routes: $$


Definition of a detour scheme

Routes are an alternating sequence of points and crossings between them. Formally, they all begin at one of the points of the set$$and end in the depot, however, it will be easier to assume that all routes are cyclic. This assumption does not change the essence, but makes all the vertices the same: in this case there are no end vertices, they are all transit.

For points$$ and route $$ set up a variable $$equal to one if in the route with number $$ truck moving from point $$ exactly $$, and zero otherwise.

Then we require, firstly, that the truck moving along the route$$ visited the point $$if she, after dividing into groups, fell into the group with the number $$:

$$

Secondly, the truck after arriving at the point $$ must leave her.

$$

You may notice that these restrictions allow the quantities $$Define routes that are a set of disjoint loops. Routes of this kind, of course, do not make sense, and a number of restrictions are required to avoid this.


Satisfying the requirements for the time of arrival of the truck at each point

In other words, you must visit the points only inside the time windows indicated by the curators. Through$$ and $$ denote, respectively, the beginning and end of the time interval in which the curator of the point $$may attend it.

To track the implementation of these restrictions, we need information about the time spent by the truck during stops and crossings on the route. Through$$ denote the duration of loading at the point $$, and through $$ - time of moving from a point $$ exactly $$ We make a reservation that $$ for all $$, and generally can be performed $$ for any $$

We introduce non-negative variables $$ and $$equal to arrival times and waiting times at the point $$ when driving along a route $$, respectively. For the entered values, the following relations should be satisfied.

The waiting time cannot be less than the time required for loading

$$

and equal to zero if the point does not belong to the route $$

$$

Arrival time at the point $$ calculated at appropriate times for the previous point $$ Here is a fairly large constant $$ used to eliminate unnecessary dependencies when moving between $$ and $$ not done.

$$

The arrival and departure of the truck must be within the interval indicated by the curator.

$$

$$

Determining the type of truck required to service each of the routes.
We denote the many types of trucks available for rent by$$ Truck type $$ characterized by body volume $$ and the cost of an hour's rent $$ Minimum truck rental time $$ denote by $$ The amount of recyclables collected at the point $$ denote by $$

We introduce variables $$equal to one if truck type $$ assigned to service route with number $$, and zero otherwise.

Integer variables$$ set the time of renting a truck type $$serving the route with number $$
For each route, $$, you must assign the type of truck:

$$

In accordance with the breakdown of points between routes, some routes may turn out to be trivial, that is, contain only depots. If the route$$ non-trivial, then the truck assigned to it is rented at least $$ hours.

$$

At the same time, the duration of the lease should also exceed the total duration of parking and moving along the route.

$$

Add restrictions providing the property: if the truck is of type $$ not assigned to a route $$, its rental time is zero.

$$

All recyclables collected at route points should fit in the back of the truck.

$$

Finally, our goal is to minimize the cost of renting trucks, which, using the designations introduced, is written as $$

Search for a solution

It is easy to verify that all the expressions involved in the optimization model are linear functions of variables, therefore, to find the exact and approximate solutions, you can use standard packages for solving mixed-integer programming problems such as Gurobi , CPLEX , Xpress , ORtools , SCIP , BLIS , etc.
We write a model for minimizing transportation costs in the GMPL language. This will allow us to use the free GLPK package for our purposes . To write code and debug the model, it will be convenient to download the GUSEK development environment , which already contains GLPK in its composition.

GUSEK looks as follows:



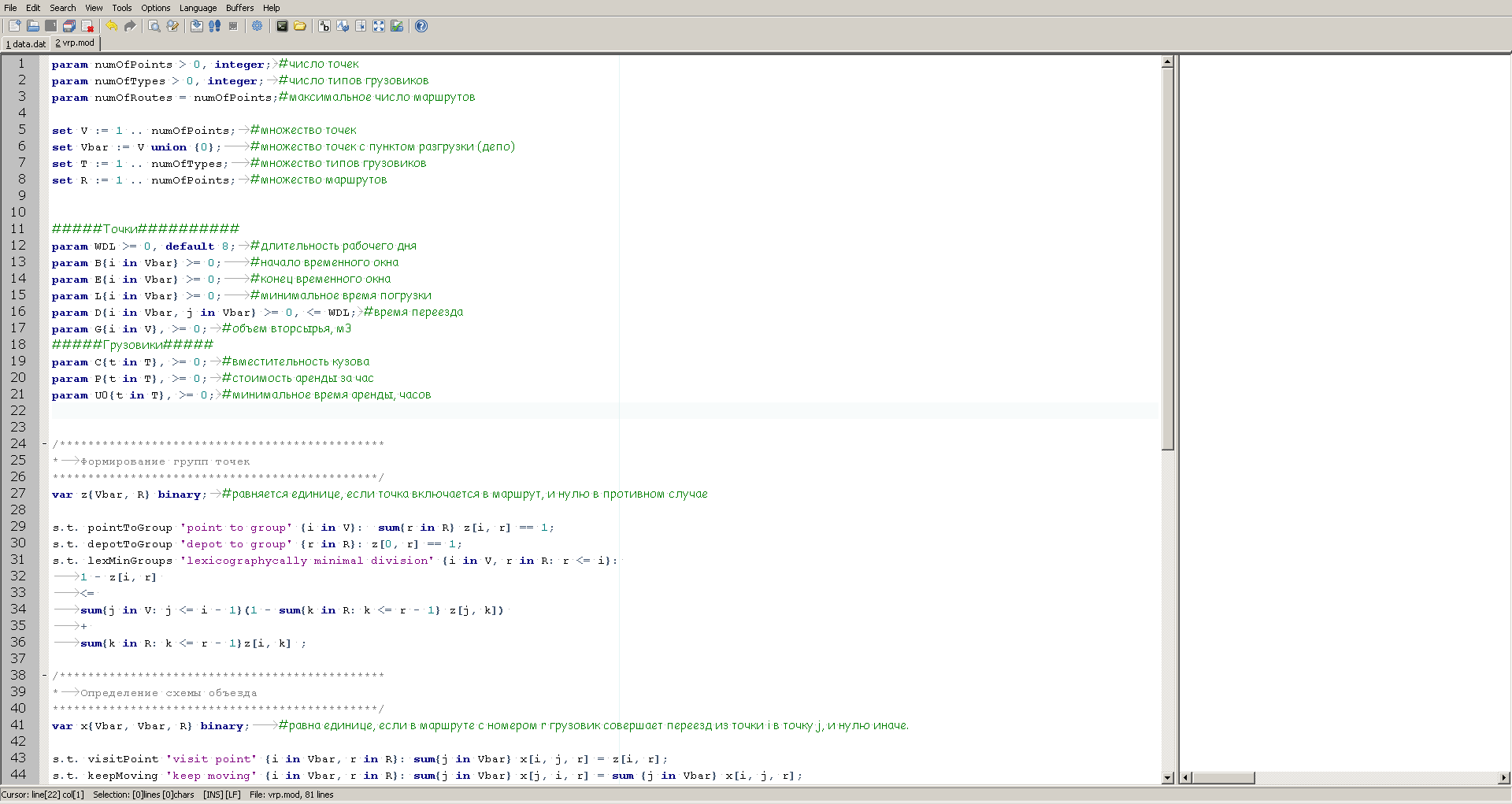
On the left we see a description of the model, and on the right there is a window for displaying information on the calculation progress, which the solver will supply after launch.


For a quick start, I’ll also add data taken from my head prepared for use in the model:


After copying the model code to a file with the name, for example, model.mod, and the input data to the data.dat file, everything is ready to run. We set a limit on the calculation time of 100 seconds (this is done using the key --tmlim [time in seconds]), transfer the path to the file with input data (using the key -d [file path]),



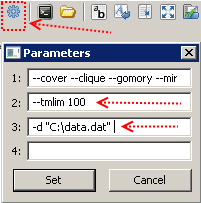
and press F5. If successful, messages will appear in the window on the right, and after a hundred seconds we will have the best solution that GLPK managed to find in the allotted time.



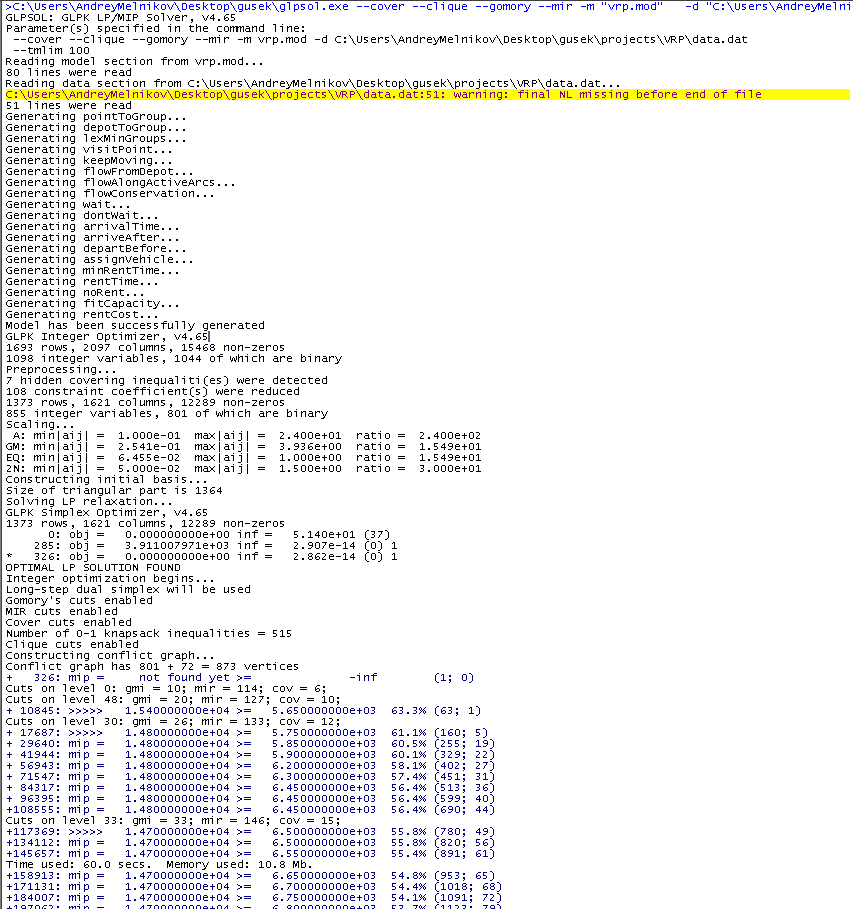
In the blue text, we are interested in the meaning after the inscription "mip =". As you can see, it decreases from time to time. All new solutions are in the process of work, the value of transport costs at the best of which is displayed in this column (there are 14700 so far). The next number is the lower bound for the best existing one, i.e.optimal solution. Initially, the estimate is significantly underestimated, but is refined over time, that is, increases. The values ​​on the left and on the right are converging, and the relative gap between them at the time of the screenshot is 54.1%. As soon as this number becomes zero, the algorithm will prove that the best solution found is the best possible. It is not always justified to wait for this event in practice, and not only because it is a long time, but it is important to make a reservation that, as a rule, a good solution is relatively quick, and the main time costs are associated with the refinement of the estimate required to prove the best possible.

Instead of a conclusion

Routing problems are extremely computationally complex, and with the increase in the number of points that need to be visited, the time required for a solver to find a solution and prove its optimality is growing rapidly. However, for fairly small examples, in a reasonable amount of time, the solver is able to build a successful set of routes and can be used to support decision-making. Analysis of the routing options proposed by the model helped us discover significant opportunities for cost reduction, and this is critical for the existence and development of the stock.

Our further efforts went towards work with uncertainty in the volumes of recyclables collected at the points. We are developing a number of stochastic programming models for making strategic and operational decisions in truck routing. If the topic turns out to be relevant and arouses interest, I will write about this too, because soon we all will have to significantly more thoroughly dive into environmental issues, which is what I wish us success in.