galinawri May 9, 2019 at 11:29 p.m.

Error Correction - Physical Constants in the Present and New Versions of the International System of Units (SI)

Transfer

March 29, 2019 - Michael Trott, Principal Researcher

Introduction

In the so-called “new SI” - an updated version of the International System of Units , which will determine seven basic units of measurement (second, meter, kilogram, ampere, kelvin, mole and candela) and which will enter into force on May 20, 2019, all SI units will be determined through the exact values of the fundamental physical constants. As a result, all of the above SI units (Newton, Volt, Ohm, Pascal, etc.) will ultimately be expressed in terms of fundamental constants. (Finally, fundamental physics will literally control our daily lives ☺)

The table below shows how everything will change from Monday evening May 20 to Tuesday morning of May 21 this year.

Computing data from this table is the goal of this blog. So, let's start with a brief overview of what will change in the new SI.

In addition to the well-known exact value of the speed of light, in four weeks another four physical constants - the Planck constant, the Boltzmann constant, the Avogadro constant and the Millikan constant (often called the elementary electric charge) - will have exact values. The decision on this change was made internationally in November last year (I wrote about it in my last

blog).

Below is a snippet of page 12 of the current draft SI brochure .

Note that in these definitions, decimal numbers are meant as exact decimal numbers, not, say, machine numbers on a computer that have finite precision and are not exact numbers. The transition frequency in the split superfine structure of Cs-133, the speed of light and "light efficiency" already have exact values today.

The world discusses future changes

This change will have some interesting consequences for other physical constants: some constants that are currently measured and have errors will become accurate, and some constants that are currently accurate will have approximate values with finite errors in the future . These changes are unavoidable to guarantee overall system consistency.

This year’s first issue of Physics of the World addressed this subject in a letter to the editor from William Hough; He wrote:

With charge fixation on the electron ( e ) and Planck's constant ( h ), all physical units are now “immortalized in stone”, which is very nice. But that raises one awkward question. Fine structure constant 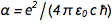, where c is the speed of light and this . From the familiar equations 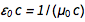, 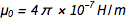we quickly find that 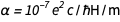. This, of course, is a pure number with a dimensionless quantity, and it is now fixed forever as equal to 1 / 137.13601, which is very close to the accepted value. This is not surprising, since the latter value would be used in the agreed new values for e and ℏ. But nature has its own value, unknown to us at present, which, because of this, is immortalized in diamond. We can be forgiven for hinting that we know better than nature. But what if the future theory of the universe becomes accepted and gives an exact value that differs significantly from the accepted value? Could this happen? There have been attempts to find a theoretical value for α , but they include menacing and controversial quantum electrodynamics.

The problem is that in the new SI system, the two

and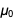

will now have inaccurate values with some error. In this blog, we will use the Wolfram Language and its knowledge of physical units and constants to see how these and other physical constants gain (or lose) error, and why this is a mathematical consequence of the definition of basic units.

A Brief Overview of the Relevant Wolfram Language Ingredients

Wolfram Language is a unique medium for conducting numerical experiments and symbolic calculations, identifying possible consequences. In addition to the general computing capabilities, three components of the system are very useful here:

1) Wolfram Language units and the structure of physical quantities.

Classical units (such as meters, feet, etc.) can be used in calculations and visualizations. And, of course, in the conversion of units of measure.

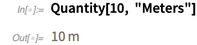
Converting to ordinary US units results in a fraction (rather than an approximate value of the real number!) Due to the well-defined ratios of the two units.

Physicists (especially) like to use "natural" units. Often these natural units are simply physical constants or combinations thereof. For example, the speed of light (natural language input is used here).

Expressed in SI units (since this is speed and units in meters and seconds are required), the speed of light has an accurate value.

On the other hand, the Planck constant does not currently have an exact value. Thus, its value, expressed in SI base units, is an approximate decimal number.

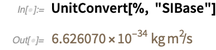
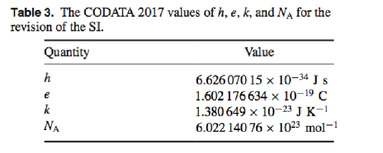
Please note that the accuracy of 6.626070 ... reflects the number of known numbers.

This is the last recommended value for the Planck constant published in CODATA 2017 in preparation for the refinement of constants. The corresponding table is presented below:

Physical constants (or combinations thereof) that link two physical quantities can often be used as natural units. The simplest examples would be the measurement of speed in terms of the speed of light or the microscopic torque in terms of ℏ . Or energy can be measured in terms of mass with an implied factor

. DimensionalCombinations Functioncan be used to search for combinations of physical constants that allow you to relate two given physical quantities. For example, the following relationships between mass and energy can be built: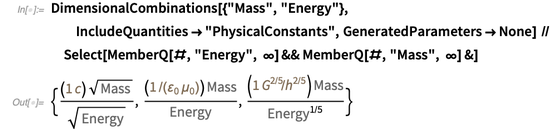

The first equality reflects Einstein's famous formula

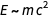, the second is the equivalent of the first relation, and the third - (dimensionally) states that

.

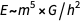2) The entity class “ PhysicalConstant ” recently added to the Wolfram Knowledgebase .

Functions and objects in the Wolfram Language are “born computationally”, that is, they are ready for use in computing. But to describe and simulate the real world, you need data about the real world. Entity structure is a convenient and fully integrated way to obtain such data. Below are some data on the electron, proton and neutron.

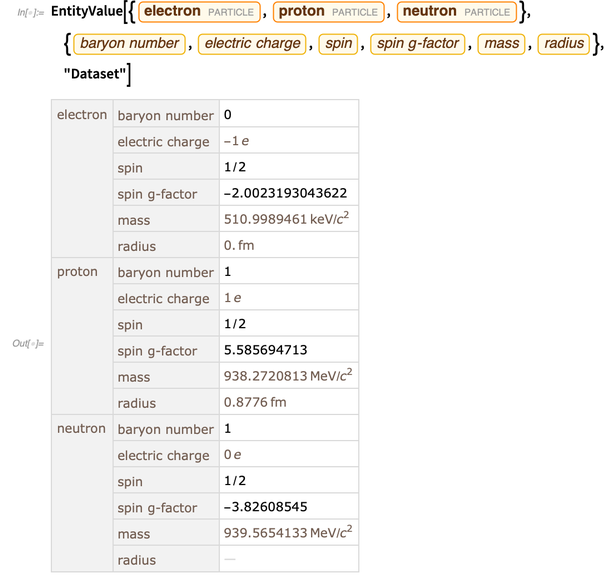
One of the new entity units is physical constants. Currently, the Knowledge Base contains more than 250 physical constants.

Below are a dozen randomly selected examples. Moreover, without a clear definition of what constants are physical constants, masses of fundamental particles, Lagrange parameters of the standard model, etc. For convenience, the list also contains astronomical constants in accordance with the Astronomical Almanac.

Most of the fundamental physical constants were called class C constants in the famous work of Jean-Marc Levy-Leblond. The constants of classes C and B are given below.

Take, for example, the natural unit of time, Planck time. The ToEntity and FromEntity functions make it easy to go back and forth between physical constants as units and physical constants as entities. An entity corresponding to a unit of Planck time is demonstrated below.

The knowledge base has a lot of meta-information about him, for example, its values in the latest CODATA lists.

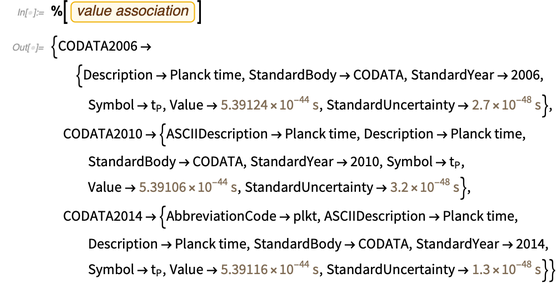
The last conclusion, which contains meaning and error, leads us to the third important function, which will be useful later:

3) Introduction of the Around [] function in version 12 of the Wolfram Language. The Around [] function provides an inaccurate value, indicating the average value and the error. The arithmetic model Around [] is based on the GUM (Guide to Expressing Measurement Error) - not to be confused with the Leibniz Plus-Minus-calculus. Here is such a value with an error.

The most important and useful aspect of computing with values that have errors is that they take correlations into account. The naive use of such values in arithmetic numbers or intervals can underestimate or overestimate the resulting error.

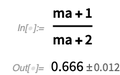
Below we see that the AroundReplace [] function takes into account correlation.

Back to the letter to the editor

Now let's use these three components and the more detailed William Hough letter to the editor.

At current approximate values for e and ℏ , these two values for the fine structure constant are consistent within the limits of their errors. The first is the expression from the letter to the editor, and the second is the quantity ( Quantity []), which represents the fine structure constant.

Every few years, CODATA publishes official values of fundamental constants (see fine structure constants ); as I said, the values used in the Wolfram Language are the latest CODATA values and the final error is reflected in the accuracy of the number.

Please note that the directly measured fine structure constant is slightly more accurate than the one that expresses the fine structure constant through other constants.

If we use the forthcoming exact values of e and ℏ , and use the current exact value

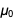, we get the following exact value for the fine structure constant in the form

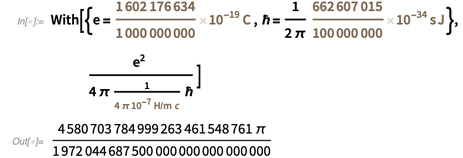
It is unlikely that the Lord, who does not even play dice , would choose such a number for significance

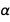in our universe. This means that while e and ℏ will be fixed in the new SI, the current exact value

and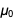

will inevitably have to be "Unlock" (see. Also Article Goldfarb on the value of

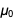the new SI). (We will return to why

and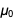

should soon become inaccurate.)

Это означает, что после 20 мая этого года эти результаты станут другими, отличающимися от приведенных ниже.

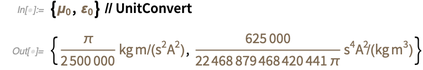
(В кратком примечании, класс сущности "PhysicalConstant" также имеет предполагаемые значения для констант, таких как константа тонкой структуры):

Теперь, если не считать теологического аргумента о точной форме постоянной тонкой структуры, с физической точки зрения, почему

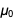должны быть неточными? В качестве аргумента вероятности давайте рассмотрим

. Один из самых выдающихся результатов, это закон Кулона.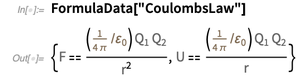

In the existing SI system, an ampere has an “exact” definition: An

ampere is the direct current that, if maintained in two parallel conductors of infinite length with an insignificant circular cross-section and placed at a distance of 1 meter in a vacuum, will create a force between these conductors equal to 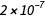Newton per meter length.

This definition uses purely mechanical quantities Newton and meter (that is, after expansion, this is a second, meter and kilogram). No relationship is made with the charge of the electron, and in the existing SI system, the elementary charge is an experimentally measured quantity.

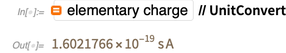
And this experimentally measured value has changed over the years, becoming more accurate.

The force on the left side of the Coulomb law (expressed in Newtons) contains the basic unit of kilogram, which, after the value of the Planck constant becomes constant, also becomes precisely definable. Since there is no reason to assume that all the laws of nature can be expressed in finite rational numbers, the only possible “moving part” in the Coulomb law will be

. Its numerical value must be determined, and it will make the left and right sides of Coulomb's law coincide.

From a more fundamental point of view of physics, the fine structure constant is the interaction constant, which determines the strength of electromagnetic interactions. And, perhaps one day, physics can calculate the value of the fine structure constant, but we are still far from this. Just choosing unit definitions cannot fix the value

.

Are the two

and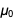

become a non-fixed, or maybe keep one of them accurate? Due to the already accurate speed of light and the ratio

, if one is

or is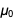

accurate, the other must also be accurate. We know that at least one must become uncommitted, so it follows that both must be uncommitted.

The values that are now given by the Planck constant, the Boltzmann constant, the Avogadro constant, and the elementary charge are neither arbitrary nor fully defined. They are determined up to approximately eight characters, so the units of measurement that they determine after May 20 correspond to the "size" of the units that they determine before May 20. But the numbers in the lower right are not defined. Thus, the value of the future exact value of the elementary charge may be

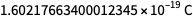, rather than

. It is Occam's razor and rationality that allow us to use

.

On a more technical level, the substitution in the previous calculation was that through the term

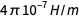in the formula the

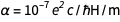ampere was used before redefinition (remember

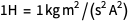), but the exact value of the elementary charge was also used, meaning the definition of ampere after redefinition. And we always need to stay in one system of units.

Calculation of error-optimized form table

So, the natural question arises: what should these “unfixed” meanings be? In my last blog, I manually created a new value

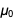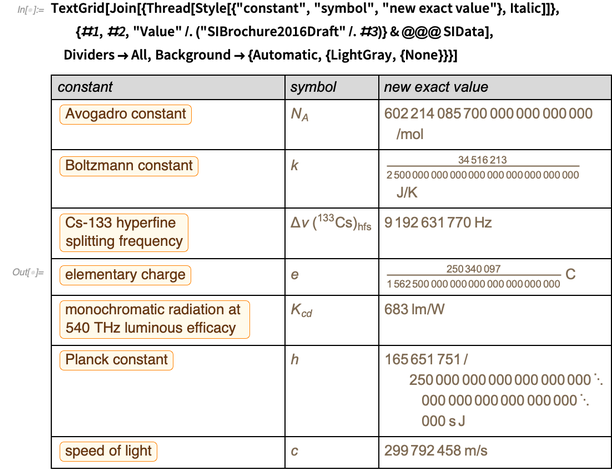
. What can be done manually can be done using a computer program, so let's implement a small program that calculates the error-optimized form of derivatives of physical constants. In a future-oriented approach, an entity class of seven constants that defines a new SI is already available.

Below are constants that will have an exact value in the new SI.

The current values of these constants together with their error (calculated using the Around [] function ) have the form:

Using the entity class “ PhysicalConstant ” we can get new, upcoming values of physical quantities. Note that, as in all computer languages, exact integers and rational numbers are either explicit integers or rational (but not decimal) numbers.

Many physical constants can be related by equations given by physical theories of various fields of physics. In the future, we want to limit ourselves to the theory of fundamental electromagnetic phenomena, in which the error of the constants will be reduced to the error of the fine structure

constant and Rydberg constant

. If we included, for example, gravitational phenomena, we would have to use the gravitational constant G, which is measured independently, although it has a very large error (which is why the NSF had the so-called " Big-G Challenge ").

Further, we restrict ourselves to electric, magnetic, and mass quantities, whose errors are reduced to units of

and

.

Below we use the new Around function to express values with corresponding errors

and

Currently, according to CODATA 2014, the relative error for

is about

, and for

about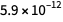

. As you can see, the error for

more than for

The following is a graph of the log base-10 relative error

as a function of a and b . Obviously, for small degrees, the relative error of the product weakly depends on the exponents a and b . This graph shows that the dependence of the error

dominates with respect to a(an indicator of the degree of fine structure). This observation is explained by the fact that the error of the Rydberg constant is 50 times less than the error of the fine structure constant.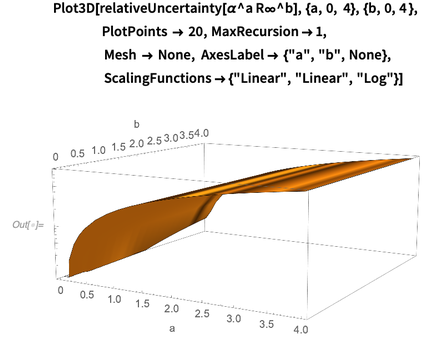

In order to calculate the errors of various constants in the new SI, we will use the following steps:

• Retrieve equivalent representations for physical constants accessible from the PhysicalConstant entity class .

These identical equalities between physical constants are the laws of physics and as such should be preserved in both the old and the new SI.

• Think of formulas as a set of algebraic equalities to which various exclusion methods can be applied to express a constant through a combination of seven basic constants of the new SI, as well as fine structure

constants and Rydberg constants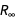

.

These are the nine basic constants that we allow to apply in the definitions of each new constant considered. (Technically, there are 10 constants in the list, but because of the simple scaling relation between h and ℏ , there are actually nine “different” constants in this list.)

The entity class “ PhysicalConstant ” contains a lot of information about the relationships between physical constants. For example, here are equivalent forms of four constants that are currently being measured and will soon be identified as having accurate values.

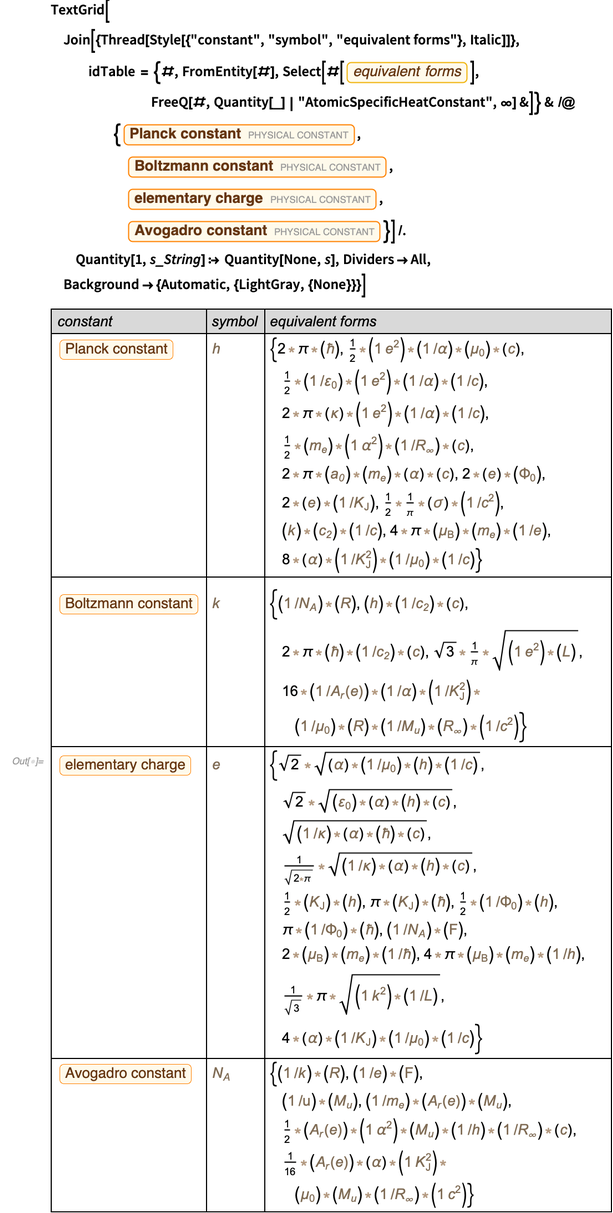
Within the accuracy of the measured values, all these unit elements work now. Here's a quick numerical check of alternative forms of the Planck constant. But the specific numerical value, especially the error, depends on the actual form of presentation. Using Around [], we can easily calculate the resulting errors.

Below is a graphical representation of the resulting errors of various representations. A very large error of dozens of representations can be traced to a large error in the second radiation constant.

And again, within the framework of the error of constants, these relations should be preserved after redefinition. So which of these representations is best used after redefinition in order to minimize errors? Perhaps none of the above equivalents is optimal, and by combining some of these ideas, it is possible to build the best one, which has a smaller resulting error.

Now, for the next steps of algebraic exceptions, we convert the constants that occur in equivalent classes (this is possible because the second arguments inEntity [" PhysicalConstant" ,. ] and in Quantity [ 1 ,. ] are equated). The reason we use entities, rather than quantities in subsequent calculations, is twofold: firstly, entities are convenient, easy-to-read representations; and secondly, algebraic functions (such as GroebnerBasis ) do not penetrate the quantities to determine the nature of their first argument.

Then we make all identities polynomial. The last step means: (1) subtracting the left side from the right side; and (2) that no fractional powers (e.g., square roots) of constants no longer appear. We carry out such a conversion to a polynomial by looking for all the fractional exponents and finding the LCM (smallest common factor) of all their denominators.

Below is one of the previous equations that contains constants with a fractional power.

After polynomialization, we come to polynomials of several variables in the three constants present. These polynomials must be eliminated.

The following table demonstrates how the toPolynomial function applies to the equivalent forms shown earlier for an elementary charge. After the canonization of ℏ in

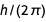, some of the resulting polynomials become identical.

Now, based on the available physical constants (without the constants used in the definition of the new SI), we get enough equivalent forms to create a set of equations.

Below is a list of the obtained polynomial equations for the expression of an elementary charge.

We express all errors through errors

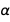and

. Only these two constants are enough to express the error of many physical constants. And since their errors are independent of each other, and since the errors are quite small, these two fairly well-known constants are best suited to express an optimized (in the sense of errors) new version of many physical constants. And, of course, we allow all seven exact constants from the new SI; since they are accurate quantities, their presence will not change the error.

The main work on the expression of a given constant through the constants and the SI

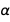, and

will be a function of GroebnerBasis . Setting the MonomialOrder -> ElventionOrder parameter is a critical step that removes all “unnecessary” physical quantities, leaving one polynomial equation with precisely defined constants and (if necessary) fine structure and Rydberg constants.

By eliminating the constants bound by the mass of the electron, we obtain

The error of this expression arises from the member

. We can define a function that removes the member

causing the error.

For a more compact representation, we can define a function that returns an equivalent form, as well as old and new errors - in the form of a string.

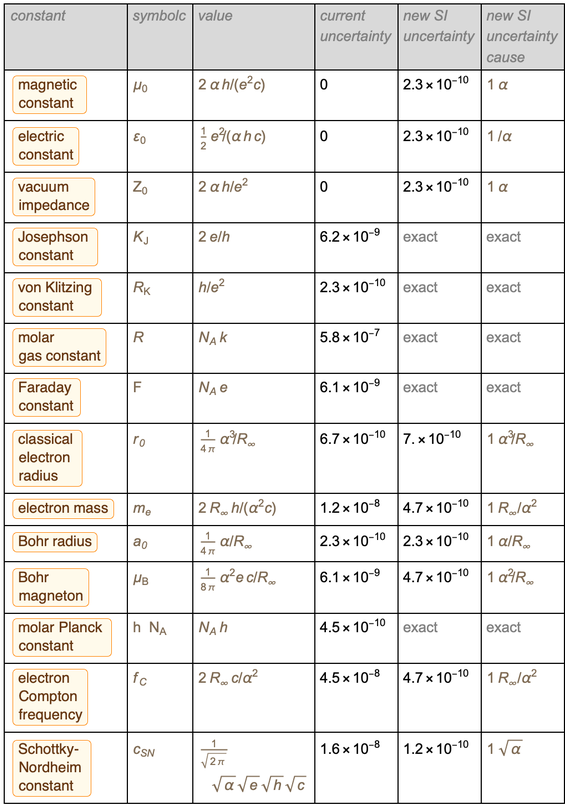
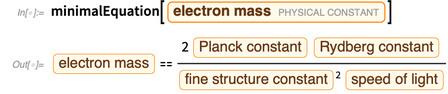
We end the blog by presenting a table of old and new errors for more than a dozen physical constants. This list is selected as a representative example; other constants can be processed in a similar way (this may require the addition of additional inaccurate constants for conservation, such as the gravitational constant or the parameters of the standard model).

Combining the rows in a table gives the following result for the optimal representation of these constants in the new SI unit system.

It was a table that we intended to display, and we managed to display it. Pay attention to the appearance

in the numerator and denominator

and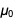

in such a way that after reduction the result

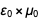becomes

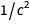. A similar list can be found at the bottom of the Wikipedia page on redefining SI units .

Now we can calmly expect 2019 World Metrology Day for a fundamentally better world, described through fundamental constants.

Download the Wolfram Notebook Blog .
Free temporary Wolfram Mathematica system
Have a question? Contact info-russia@wolfram.com

Tags: