Intro Newton Protocol: what can fit in 4 kilobytes

I recently competed in the Revision 2019 demo scene in the PC 4k intro category, and my intro won first place. I did coding and graphics, and dixan composed music. The basic rule of the competition is to create an executable file or website that is only 4096 bytes in size. This means that everything has to be generated using mathematics and algorithms; in no other way you can squeeze images, video and audio into such a tiny amount of memory. In this article, I will talk about the rendering pipeline of my Newton intro intro. Below you can see the finished result, or click here to see how it looked live on Revision, or go to pouetto comment and download the participating intro. You can read about competitors' work and corrections here .


The Ray marching distance fields technique is very popular in the 4k intro discipline because it allows you to specify complex forms in just a few lines of code. However, the disadvantage of this approach is the speed of execution. To render the scene, you need to find the point of intersection of the rays with the scene, first determine what you see, for example, a ray from the camera, and then subsequent rays from the object to the light sources to calculate the lighting. When working with ray marching, these intersections cannot be found in one step, you need to take many small steps along the beam and evaluate all objects at each point. On the other hand, when using ray tracing, you can find the exact intersection by checking each object only once, but there is a very limited set of shapes that you can use:

In this intro, I wanted to simulate very accurate lighting. Since for this it was necessary to reflect millions of rays in the scene, ray tracing seemed to be a logical choice to achieve this effect. I limited myself to a single figure - a sphere, because the intersection of a ray and a sphere is calculated quite simply. Even the walls in the intro are actually very large spheres. In addition, it simplified the simulation of physics; it was enough to take into account only collisions between the spheres.

To illustrate the amount of code that fits in 4096 bytes, below I presented the complete source code of the finished intro. All parts except the HTML at the end are encoded as a PNG image to compress them to a smaller size. Without this compression, the code would take up almost 8900 bytes. The part called Synth is a stripped down version of SoundBox.. I used the Google Closure Compiler and the Shader Minifier to package the code in this minimized format . In the end, almost everything is compressed into PNG using JsExe . The full compilation pipeline can be seen in the source code of my previous 4k intro Core Critical , because it completely matches the one presented here.


Music and synthesizer are fully implemented in Javascript. The part on WebGL is divided into two parts (highlighted in green in the code); she sets up the render pipeline. The physics and ray tracer elements are GLSL shaders. The rest of the code is encoded in a PNG image, and HTML is added to the end of the resulting image unchanged. The browser ignores the image data and only executes the HTML code, which in turn decodes the PNG back into javascript and executes it.

Rendering pipeline

The image below shows the rendering pipeline. It consists of two parts. The first part of the pipeline is a physics simulator. The intro scene contains 50 spheres colliding with each other inside the room. The room itself is composed of six spheres, some of which are smaller than others to create more curved walls. Two vertical light sources in the corners are also spheres, that is, a total of 58 spheres in the scene. The second part of the pipeline is the ray tracer, which renders the scene. The diagram below shows the rendering of one frame at time t. The physics simulation takes the previous frame (t-1) and simulates the current state. The ray tracer takes the current positions and positions of the previous frame (for the speed channel) and renders the scene. Then post-processing combines the previous 5 frames and the current frame to reduce distortion and noise,


Rendering a frame at time t.

The physical part is quite simple, on the Internet you can find many tutorials on creating primitive simulations for spheres. Position, radius, speed and mass are stored in two textures with a resolution of 1 x 58. I used the Webgl 2 functionality, which allows rendering to multiple render targets, so the data of two textures are recorded simultaneously. The same functionality is used by the ray tracer to create three textures. Webgl does not provide any access to the NVidia RTX or DirectX Raytracing (DXR) ray tracing APIs, so everything is done from scratch.

Ray tracer

Ray tracing itself is a fairly primitive technique. We release a ray into the scene, it is reflected 4 times, and if it gets into the light source, the color of the reflections accumulates; otherwise, we get black. In 4096 bytes (which include music, synthesizer, physics, and rendering) there is no room for creating complex accelerating ray-tracing structures. Therefore, we use the brute-force method, that is, we check all 57 spheres (the front wall is excluded) for each ray, without making any optimizations to exclude part of the spheres. This means that to provide 60 frames per second in 1080p resolution, you can emit only 2-6 rays, or samples per pixel. This is close enough to create a smooth lighting.


1 sample per pixel.


6 samples per pixel.

How to cope with this? At first I investigated the ray tracing algorithm, but it was already simplified utterly. I managed to increase the performance a bit by eliminating the cases when the ray begins inside the sphere, because such cases are applicable only in the presence of transparency effects, and only opaque objects were present in our scene. After that, I combined each if condition into a separate statement to avoid unnecessary branching: despite the “unnecessary” calculations, this approach is still faster than a bunch of conditional statements. You could also improve the sampling pattern: instead of emitting rays randomly, we could distribute them across the scene in a more even pattern. Unfortunately, this did not help and led to wavy artifacts in every algorithm I tried. However, this approach created good results for still images. As a result, I returned to using a completely random distribution.

Neighboring pixels should have very similar lighting, so why not use them to calculate the lighting of a single pixel? We do not want to blur textures, only lighting, so we need to render them in separate channels. Also, we don’t want to blur objects, so we need to consider the identifiers of objects in order to know which pixels can be blurred easily. Since we have light-reflecting objects and we need clear reflections, it’s not enough just to find out the ID of the first object that the beam collides with. I used a special case for pure reflective materials to also include the IDs of the first and second objects visible in reflections in the object identifier channel. In this case, blurring can smooth out lighting in objects in reflections, while maintaining the boundaries of objects.


Texture channel, we do not need to blur it.


Here in the red channel contains the ID of the first object, in green - the second, and in blue - the third. In practice, all of them are encoded into a single value of the float format, in which the integer part stores the identifiers of objects, and the fractional one indicates roughness: 332211.RR.

Since there are objects with different roughness in the scene (some areas are rough, the light is scattered on others, in the third there is a mirror reflection), I store the roughness to control the blur radius. There are no small details in the scene, so I used a large 50x50 core with blur in the form of inverse squares for blurring. It does not take into account world space (this could be realized in order to obtain more accurate results), because on surfaces located at an angle in some directions, it erodes a larger area. Such blurring creates a fairly smooth image, but artifacts are clearly visible, especially in motion.


Lighting channel with blur and still noticeable artifacts. In this image, blurry dots on the back wall are visible, which are caused by a small bug with the identifiers of the second reflected object (the rays leave the scene). On the finished image, this is not very noticeable, because clear reflections are taken from the texture channel. Lighting sources also become blurry, but I liked this effect and I left it. If desired, this can be prevented by changing the identifiers of objects depending on the material.

When objects are in the scene and the camera shooting the scene moves slowly, the lighting in each frame should remain constant. Therefore, we can perform blur not only in the XY coordinates of the screen; we can blur in time. If we assume that the lighting does not change too much in 100 ms, then we can average it for 6 frames. But during this time window, the objects and the camera will still go some distance, so a simple calculation of the average for 6 frames will create a very blurry image. However, we know where all the objects and the camera were in the previous map, so we can calculate the velocity vectors in the screen space. This is called temporary reprojection. If I have a pixel at time t, then I can take the speed of that pixel and calculate where it was at time t-1, and then calculate, where the pixel at time t-1 is at time t-2, and so on, back 5 frames. Unlike blur in screen space, I used the same weight for each frame here, i.e. just averaged the color between all frames for a temporary “blur”.


A pixel velocity channel reporting where the pixel was in the last frame based on the movement of the object and camera.


To avoid joint blurring of objects, we will again use the channel of object identifiers. In this case, we take into account only the first object that the beam collided with. This provides anti-aliasing within the object, i.e. in reflections.

Of course, the pixel might not be visible in the previous frame; it could be hidden by another object or be out of the camera's field of view. In such cases, we cannot use the previous information. This check is performed separately for each frame, so we get from 1 to 6 samples or frames per pixel, and use those that are possible. The figure below shows that for slow objects this is not a very serious problem.


When objects move and open new parts of the scene, we do not have 6 frames of information to average it for these parts. This image shows areas that have 6 frames (white), as well as those in which they are missing (gradually darkening shades). The appearance of the contours is caused by the randomization of the sampling locations for the pixel in each frame and the fact that we take the identifier of the object from the first sample.


Blurred lighting is averaged over six frames. Artifacts are almost invisible and the result is stable over time, because in each frame only one frame out of six changes in which lighting is taken into account.

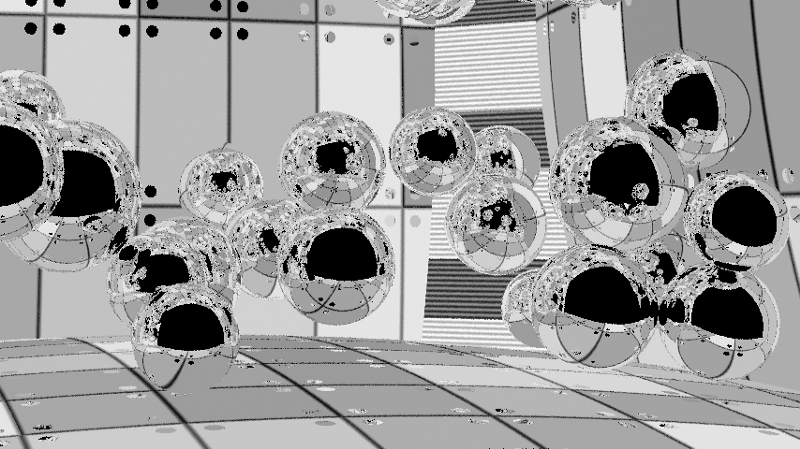
Combining all this, we get a finished image. Lighting is blurred to adjacent pixels, while textures and reflections remain clear. Then all this is averaged between six frames to create an even smoother and more stable image over time.


The finished image.

Attenuation artifacts are still noticeable, because I averaged several samples per pixel, although I took the channel of the object identifier and speed for the first intersection. You can try to fix this and get smoothing in the reflections, discarding the samples if they do not coincide with the first, or at least if the first collision does not coincide in order. In practice, the traces are almost invisible, so I did not bother to eliminate them. The boundaries of objects are also distorted, because the channels of speed and object identifiers cannot be smoothed. I considered the possibility of rendering the entire image in 2160p resolution with a further reduction in scale to 1080p, but my NVidia GTX 980ti is not capable of processing such resolutions with a frequency of 60fps, so I decided to abandon this idea.

In general, I am very pleased with how the intro turned out. I managed to squeeze into it everything that I had in mind, and despite minor bugs, the final result was very high quality. In the future, you can try to fix bugs and improve anti-aliasing. It is also worth experimenting with features such as transparency, motion blur, various shapes and object transformations.