A math duo mapped an endless territory of minimal surfaces
- Transfer
A couple of mathematicians on the basis of a little-known mathematical theory of 30 years ago demonstrated that minimal surfaces resembling a soap film appear in large numbers on a wide range of figures

At the end of 2011, Brian White occasionally heard a knock at the door of his Stanford office. Outside, at these moments, two young mathematicians were waiting for him, Fernando Coda Marquez and Andre Nevis , who always had about the same question: would White have a few minutes to help them figure out one of the obscure parts of a little-known dissertation for several hundred pages written thirty years ago?
In a dissertation written by John Pitts, a powerful mechanism for constructing minimal surfaces - structures similar to soap film and bubbles - was presented within a wide range of shapes. When a minimal surface can be constructed on a figure, the latter makes it possible to study the geometry of the space surrounding it. Such surfaces appear in various scientific problems, from the study of black holes to the development of biomolecules.
And yet, all these years, Pitts' dissertation has fallen outside the realm of scholars ’attention - perhaps because it was incredibly difficult to read. Marquez and Nevis were convinced that there was great potential in it. “It was obvious to us that this theory was completely underestimated and went unnoticed,” said Nevis, who is now a professor at the University of Chicago.
Although White never once asked the couple why they were interested in Pitts' work, they each time stated that their interest was “purely academic,” Nevis said. However, they had a definite goal - to prove Wilmore’s hypothesis 50 years ago, which addresses the issue of finding the best possible donut shape (details later). After three months of struggling with the ideas from Pitts' dissertation, Marquez and Nevis achieved their goal , earning many awards and positive reviews.
But in the past few years, they have been able to push Pitts ideas far further. Pitts, with his curator, Frederick Almgren, found a way to ensure that each figure in a small number of dimensions has at least one minimum surface. Now, Marquez and Nevis, using the cohort of young mathematicians gathered around them, based on the ideas of Almgren and Pitts, have shown that in the general case these forms should contain many minimal surfaces - infinitely many surfaces crowding and crowding in all corners of the figures. “This is a huge breakthrough,” the famous geometer Karen Uhlenbeck from the University of Texas wrote to us in an email .
“It takes a lot of effort to create a single minimal surface,” said Richard Shoin.from the University of California, Irvine, who advised Nevis about 15 years ago. “The fact that there are so many of them is amazing.”
This renaissance of the theory of Almgren and Pitts has led to an explosion of activity in the last couple of years. “The results are so fast and in such large numbers that it’s hard to keep track of them,” White said. “It seems very interesting and wonderful to me.”
Marking the mountain range
Dip the curved wire into a soap solution, or blow a soap bubble, and the liquid will quickly form the surface of the smallest possible area. The geometry of these minimal surfaces has occupied mathematicians for hundreds of years. They appear in various fields, from architecture, where the minimal surface inspires the design of roofs and other structures, to the creation of microparticles for drug delivery. Five years ago, when a team of scientists created porous molecules capable of carrying drugs or hormones inside themselves, they found that some molecules took the form of a gyroid , an endlessly repeating surface, some parts of which resemble a soap film.
Technically, mathematicians consider only soap films on a wire as surfaces with a minimum surface, but not soap bubbles, because in an abstract space where there are no air molecules, the bubble would deflate to a point. However, the film on the wire does not fully satisfy mathematicians. Its inner part is a smooth surface, but its wire breaks off sharply. It is logical to think about whether it is possible to extend this surface beyond the boundaries of wire boundaries so that it continues to look like a soap film in each individual area. Sometimes this is possible, and the surface stretches to infinity. Sometimes the surface comes back and awkwardly intersects with itself, or meets other difficulties.

A gyroid is a type of minimal surface that arose during the design of microparticles for drug delivery.
In ordinary space, this exhausts all the possibilities. But mathematicians and other scientists often consider other worlds that are different from the infinite three-dimensional space we are used to - curved or finite, such as three-dimensional analogies of a sphere or surface of a torus. Such figures have new interesting possibilities: minimal surfaces that bend on themselves and lock into a closed final figure that does not require wire support.
In the theory of relativity, these finite minimal surfaces play the role of the event horizon of black holes. And if they can be found on any figure, this helps mathematicians to consider their geometry from different sides: they give a template for cutting the figure (or manifold ) into potentially simpler pieces, they indicate areas of positive curvature within the manifold - into sections, curving inward, like a sphere or a black hole, as opposed to curving outward.
“We know little about manifolds with positive curvature,” said Shoin.
However, it is often difficult to prove the existence of a minimal surface within a figure. To understand why so, consider a two-dimensional version of this problem. The question of finding the minimum surface makes sense in any dimension: mathematicians simply consider the surface to be a form whose dimension is one less than the space in which it lives. So in a two-dimensional world, the “geodesic” curves made up of the shortest paths connecting nearby points will be the minimum surface.
For some two-dimensional figures, easily find geodesic curves closed in a finite loop. Take the surface of a torus - not even necessarily even and symmetrical; let it have irregularities and bulges. If we wrap such a donut with an elastic band passing through its center, we can imagine how we tighten it and shift it to various possible positions. One of them will be the shortest - it will be a geodesic curve by definition.
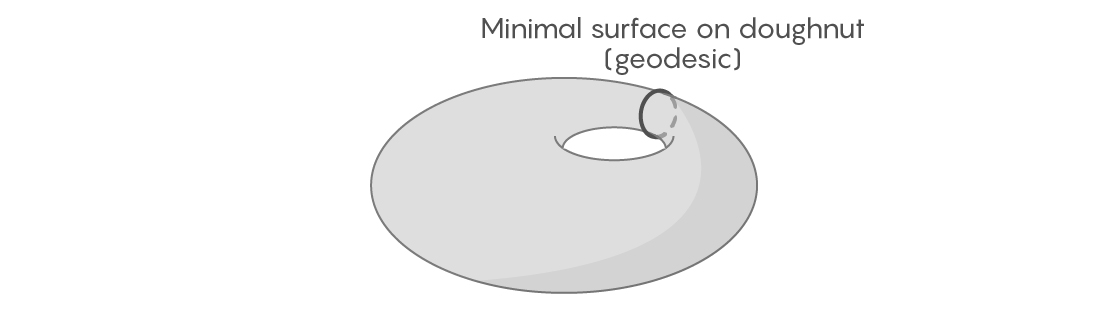
But if the sphere is our figure, this approach will no longer work. On a perfectly flat sphere, it is easy to find a geodesic curve - it will be the equator and other full circles. But on an uneven sphere, for example, on the surface of the Earth, it is not clear where the geodesic curves go and whether any of them are closed in a loop. You can imagine how we wrap the earth with an elastic band, as in the case of a donut. But if you start moving it, trying to shorten it, it will shrink to one point, because unlike a donut, the sphere does not have a hole for the elastic to cling to.
However, this fiasco with an elastic band is fraught with the germ of success. If the equator of a round sphere is intercepted by an elastic band, then the only way to shift it - to add waves to it - will make it longer. If you move it differently, up or down to a new latitude, it will become shorter. Therefore, the equator will be the shortest curve from one point of view, and the longest from the other.
This makes the equator related to the saddle of the mountain pass, the highest point on one side (from the path through the mountains) and the lowest on the other (from the path to nearby peaks). And this is not just a weak analogy: as a rule, minimal surfaces turn out to be such saddles, but their mountain ranges live in a world that is much harder to visualize.
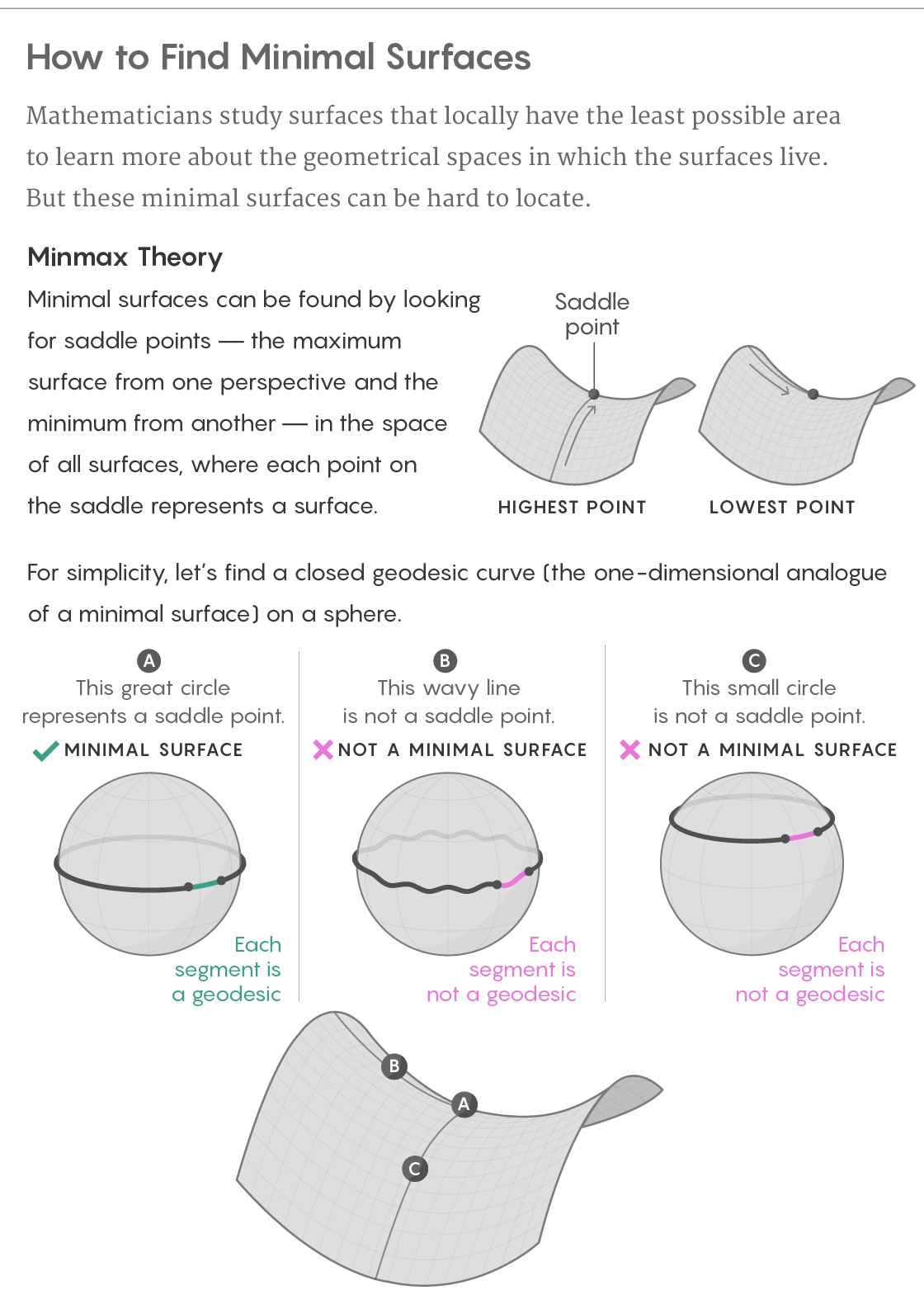
Determining the minimum surface of a figure, we can consider a new world consisting of all possible finite surfaces existing within this figure - we will call it the “surface of surfaces”. Each point of the surface space corresponds to the entire surface entirely on the original figure. Then we can consider the area of each surface as the height of the corresponding point in the space of surfaces, as a result of which our world will have a natural topography. The search for minimal surfaces on the original figure becomes the search for saddles in the surface space.
In 1917, George David Birkhoff took this approach, to show that any sphere, hilly or smooth, there is sure to be one closed geodesic curve. About six decades later, Almgren and Pitts masterfully expanded Birkhoff's ideas by marking the surface topography of surfaces on all finite figures in dimensions from three to seven, and then used this topography to prove that such figures always have at least one closed minimal surface. Pitts’s dissertation from 1981 on this Minmax theory — so named because the saddle is both a minimum and a maximum — was “absolutely amazing,” Nevis said.
However, it was extremely complex. Few people understood the nuances of the theory, and some mathematicians who studied it claimed that it was not fully confirmed, Shoin said. “I don’t think there was any doubt that it was extremely interesting and important,” he said. “But it was unclear how full it was.”
Work on the Minmax theory gradually came to naught. “Pitts’s work has been forgotten by the mathematical community for about 30 years,” Nevis said. She was not resurrected until Nevis and Marquez met in 2006 in the elevator of the mathematical building of Princeton University.
Over the mountain pass
At that moment, Marquez arrived at Princeton to give a lecture; Nevis got a job there shortly after defending a doctorate. Both had Portuguese as their native language (Marquez was from Brazil and Nevis was from Portugal), and they easily found a common language. “Then I talked to him for the first time, but he talked with me as if we had been friends for 10 years,” recalls Marquez, now a professor at Princeton.
Then they found that discussing mathematical ideas was just as natural for them. They have different styles: Marquez is more calm, and Nevis is more intense. But this served as a plus for them. “It's very rare to find someone who complements you so well,” said Marquez.
Both were eager to find some complex mathematical problem that could be immersed in. For several years, the couple threw ideas every time their paths crossed to “see what was delayed,” Nevis said. “We had a million ideas, and as a result, one of them was filtered out and turned into something formed.”
The filtered out problem turned out to be the famous problem of the “Wilmore hypothesis”. She suggests finding a torus shape that minimizes the magnitude known as the Willmore energy, which, roughly speaking, measures the difference between a given shape and a circular sphere. In 1965, Wilmore suggested that it would be the most round donut of a particularly symmetrical shape, known as Clifford's torus.However, despite many attempts, the hypothesis was not proven to anyone.

Marquez (left) and Nevis
Marquez and Nevis developed a promising approach, but to work it, they needed the last ingredient: minimax theory. They thought that mastering this theory and writing the final work would take two to three weeks - until they opened the book of Pitts. “We were shocked - what is it all about? - said Nevis. “The book was incredibly dry.”
Separate theorems grew into many pages - and this was only a description of the theorems, not their proof. The main theorem was simply hard to find. “I remember how Fernando came to my office and said: I found the statement of the theorem!” - said Nevis.

Thor Clifford
When they got stuck, they poker and ask White for help, one of the few people who understood most of Pitts’s work (although White himself described these conversations as “blind, leading blind”; Pitts himself, a professor at A&M University of Texas, graduated write works on the theory of minmax a few decades ago). “We were incredibly motivated, and so we were able to break through,” Nevis recalls. “But that was not a task for the faint of heart.”
By the time Marquez and Nevis finished their proof of Wilmore's hypothesis, they understood the Minmax theory better than any other mathematician. They were convinced that its potential extends much further than the very statement of the hypothesis. “We knew we had a very powerful theory,” Nevis said. - Each time, using the method to prove a certain result that has remained open for a long time, you understand that there is something in it. This suggests that it’s worth continuing to dig further. ”
The minmax diagram from Almgren and Pitts produces not just one saddle, but an infinite number of them. In theory, this should correspond to an infinite number of minimal surfaces of the original shape. But Almgren and Pitts could not show that the minimal surfaces obtained in this way were different. Therefore, the only thing that could definitely be said was that each figure had at least one minimal surface.
After that, “the development of the topic has practically stopped,” Nevis said. “It was the best result for a period of more than 30 years.”
A new ingredient was needed, and Marquez and Nevis found it. The endless list of minmax surfaces, as they showed in 2016, behaves the same as the frequencies of the drum.
The mathematician German Weil in 1911 showed that the fundamental frequencies of the drum have one unexpected property: roughly speaking, high frequencies depend only on the volume of the drum, and not on its shape. Marquez and Nevis, together with Eugene Lekumovich of the Massachusetts Institute of Technology, showed that Minmax surfaces satisfy a mathematical law similar to the law of drum frequencies. In particular, surface areas are roughly determined by the amount of space in which they live, and not by its shape.
This result, which put an end to the hypothesis put forward several decades ago, allowed Marquez and Nevis to show in 2017 - this time Kay Airi helped themfrom the University of Tokyo - that for most figures, the list of minmax contains an infinite number of different minimal surfaces. Moreover, they showed that these surfaces are “dense”: they appear next to each point in the surrounding space. The intuition supporting this conclusion is that in order for the volume of space to determine the areas of the location of minimal surfaces, the latter must somehow “see” the entire volume. And this "says that these guys are in all their diversity," said Marquez.
A couple of months later, this couple, together with Marques graduate student Antoine Sun , showed that if you go through the list of minmax surfaces, you will see that they fill the space evenly- What mathematicians call "equidistribution" is manifested.
“When I heard that they were equally distributed, I was amazed,” White said. “It seemed that people should not have been able to prove such a result during my lifetime.”
In the last couple of years, several more mathematicians have joined the question. For example, in January, Xin Zhou from the University of California at Santa Barbara, based on previous work by Marquez and Nevis, proved that for most figures all the minimal surfaces on the Almgren and Pitts list are different from each other, which put a nice point on this issue. “This really nicely closes this topic, open since the days of Almgren and Pitts in the 80s,” White said.
This family of results takes into account almost every figure in dimensions from three to seven - with the exception of the smoothest forms, no matter how counterintuitive. But last June, Sunn was able to prove that each figure in these dimensions, including the most rounded ones, has infinitely many closed minimal surfaces, which confirmed another hypothesis that is several decades old.
It is still unclear whether the density and equidistribution will behave as uniformly, as well as how the minmax theory does not work in compact manifolds, or in eight or more dimensions (however, the new work has achieved some success here too). Mathematicians predict that we will be able to answer many questions sooner than it seemed.
“Everything is developing extremely fast,” Nevis said. “Every week I look at the site with arxiv preprints, and I see there how someone decided something else.”
From one point of view, these works mark the end - or the end - of a story that has hung in its unfinished state for almost four decades. But this is also a new beginning: mathematicians are just beginning to understand that these new ideas regarding minimal surfaces can tell us about the spaces in which they live.
“I can well assume that other interesting ways of applying this knowledge will appear soon, but what exactly, I definitely can’t say,” said Shoin. “I’m sure that this will be one of the main directions in geometry.”
