Versatile and perfect hashing
We start the week with useful material dedicated to the launch of the course "Algorithms for Developers" . Have a good reading.

1. Overview
Hashing is an excellent practical tool, with an interesting and subtle theory. In addition to using data as a vocabulary structure, hashing is also found in many different areas, including cryptography and complexity theory. In this lecture, we describe two important concepts: universal hashing (also known as universal family of hash functions) and ideal hashing.
The material highlighted in this lecture includes:
2. Introduction
We will consider the main problem with the dictionary, which we discussed before, and consider two versions: static and dynamic:
For the first problem, we could use a sorted array and a binary search. For the second, we could use a balanced search tree. However, hashing provides an alternative approach, which is often the fastest and most convenient way to solve these problems. For example, suppose you are writing a program for AI search and want to store situations that you have already resolved (positions on the board or elements of the state space) so as not to repeat the same calculations when you run into them again. Hashing provides an easy way to store this information. There are also many applications in cryptography, networks, complexity theory.
3. The basics of hashing The
formal formulation for hashing is as follows.
One of the great things about hashing is that all dictionary operations are incredibly easy to implement. To search for the key x, simply calculate the index i = h (x) and then go through the list in A [i] until you find it (or exit the list). To insert, simply place a new item at the top of its list. To delete, you just need to perform the delete operation in the linked list. Now we turn to the question: what do we need to achieve good performance?
Desirable properties. Key desirable properties for a good hash scheme:
Given this, the search time for the element x is O (the size of the list is A [h (x)]). The same is true for deletions. Insertions take O (1) time regardless of the length of the lists. So, we want to analyze how big these lists are.
Basic intuition: one way to distribute elements beautifully is to distribute them randomly. Unfortunately, we cannot just use the random number generator to decide where to direct the next element, because then we can never find it again. So, we want h to be something “pseudo-random” in some formal sense.
Now we will present some bad news, and then some good news.
Statement 1 (Bad News) For any hash function h if | U | ≥ (N −1) M +1, there is a set S of N elements that all hashed in one place.
Proof: by the Dirichlet principle. In particular, to consider counterpoints, if each location had no more than N - 1 elements of U that hash it, then U could have a size of no more than M (N - 1).
This is partly why hashing seems so mysterious - how can it be argued that hashing is good if for any hash function you can think of ways to prevent it? One answer is that there are many simple hash functions that work well in practice for typical S sets. But what if we want a good guarantee of the worst case?
Here's the key idea: let's use randomization in our h construct, similar to randomized quicksort. (Needless to say, h will be a deterministic function). We will show that for any sequence of insertion and search operations (we do not need to assume that the set of inserted elements S is random), if we choose h in this probabilistic way, the performance of h in this sequence will be good in anticipation. Thus, this is the same guarantee as in randomized quicksort or traps. In particular, this is the idea of universal hashing.
Once we develop this idea, we will use it for a particularly enjoyable application called “perfect hashing”.
4. Universal hashing
Definition 1. The randomized algorithm H for constructing the hash functions h: U → {1, ..., M} is
universal if for all x! = Y in U we have

We can also say that the set H of hash functions is a universal hash family functions if the procedure “choose h ∈ H at random” is universal. (Here we identify the set of functions with a uniform distribution over the set.)
Theorem 2. If H is universal, then for any set S ⊆ U of size N, for any x ∈ U (for example, which we could look for), if we construct h randomly Thus, in accordance with H, the expected number of collisions between x and other elements in S is no more than N / M.
Proof: each y ∈ S (y! = X) has at most 1 / M chance of a collision with x by the definition of “universal”. So,
Now we get the following corollary.
Corollary 3. If H is universal, then for any sequence of insertion, search, and deletion operations L, in which there can be no more than M elements in a system at a time, the expected total cost of L operations for a random h ∈ H is only O (L) (viewing the time to calculate h as constants).
Proof: for any given operation in the sequence, its expected cost is constant by Theorem 2, so the expected total cost of L operations is O (L) in linearity of expectation.
Question: can we actually build a universal H? If not, then this is all pretty pointless. Fortunately, the answer is yes.
4.1. Creating a universal hash family: matrix method
Suppose the keys are u-bits long. Say, the size of table M is equal to degree 2; therefore, the index is b-bit long with M = 2b.
What we will do is choose h as the random matrix 0/1 b-by-u and define h (x) = hx, where we add mod 2. These matrices are short and thick. For example:
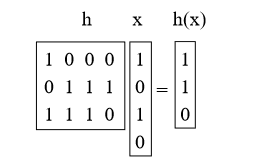
Proposition 4. For x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.
Proof: First, what does multiplying h by x mean? We can think of it as adding some of the columns h (doing vector addition mod 2), where 1 bit in x indicates which ones to add. (for example, we added the 1st and 3rd columns of h above)
Now take an arbitrary key pair x, y such that x! = Y. They should be different somewhere, so, say, they differ in the i-th coordinate, and for concreteness we say xi = 0 and yi = 1. Imagine that we first selected all h except the i-th column. For the remaining samples of the ith column, h (x) is fixed. However, each of 2b different settings of the ith column gives a different value of h (y) (in particular, every time we turn a bit in this column, we turn the corresponding bit into h (y)). So there is exactly a 1 / 2b chance that h (x) = h (y).
There are other methods for constructing universal hash families, which are also based on the multiplication of primes (see Section 6.1).
The next question that we will consider: if we correct the set S, can we find a hash function h such that all searches will have constant time? The answer is yes, and this leads to the topic of perfect hashing.
5. Perfect Hashing
We say that a hash function is ideal for S if all searches occur in O (1). Here are two ways to build ideal hash functions for a given set S.
5.1 Method 1: a solution in O (N2) space
Let's say we want to have a table whose size is quadratic in size N of our dictionary S. Then here is a simple method for constructing an ideal hash function . Let H be universal and M = N2. Then just pick a random h from H and try it! The statement is that there is at least a 50% chance that she will not have collisions.
Proposition 5. If H is universal and M = N2, then Prh∼H (no collisions in S) ≥ 1/2.
Proof:
• How many pairs (x, y) are there in S? Answer:
• For each pair, the probability of their collision is ≤ 1 / M by definition of universality.
• So Pr (there is a collision) ≤ / M <1/2.
/ M <1/2.
This is like the other side of the "birthday paradox." If the number of days is much larger than the number of people squared, then there is a reasonable chance that no couple will have the same birthday.
So, we just pick a random h from H, and if any collisions arise, we just pick a new h. On average, we will only need to do this twice. Now, what if we want to use only the O (N) space?
5.2 Method 2: a solution in the space O (N)
The question of whether it is possible to achieve perfect hashing in O (N) space has been open for some time: "Should the tables be sorted?" That is, for a fixed set, you can get a constant search time only with linear space? There was a series of more and more complex attempts, until finally it was solved using the good idea of universal hash functions in a two-level scheme.
The method is as follows. First, we will hash into a table of size N using universal hashing. This will lead to some collisions (unless we are lucky). However, then we rehash each basket using method 1, squaring the basket size to get zero collisions. Thus, the scheme consists in the fact that we have a hash function of the first level h and a table A of the first level, and then N hash functions of the second level h1, ..., hN and N of the second level table A1, ..., A.N ... To find the element x, we first compute i = h (x), and then find the element in Ai [hi (x)]. (If you did this in practice, you could set the flag so that you would take the second step only if there really were conflicts with the index i, otherwise you would just put x itself in A [i], but let's let's not worry about it here.)
Say a hash function h hashes n elements of S to location i. We have already proved (by analyzing method 1) that we can find h1, ..., hN, so that the total space used in the secondary tables is Pi (ni) 2. It remains to show that we can find a first-level function h such that Pi (ni) 2 = O (N). In fact, we show the following:
Theorem 6. If we choose the starting point h from the universal set H, then
Evidence. Let us prove this by showing that E [Pi (ni) 2] <2N. This implies what we want from Markov inequality. (If there were a probability of even 1/2 that the amount could be more than 4N, this fact alone would mean that the expectation should be more than 2N. Thus, if the expectation is less than 2N, the probability of failure should be less 1/2.)
Now, the tricky trick is that one way to calculate this amount is to count the number of ordered pairs that have a collision, including collisions with oneself. For example, if the basket has {d, e, f}, then d will have a conflict with each of {d, e, f}, e will have a conflict with each of {d, e, f}, and f will have a conflict with each of {d, e, f}, so we get 9. So, we have:
So, we just try a random h from H until we find one such that Pi n2 i <4N, and then fixing this function h, we find N secondary hash functions h1, ..., hN as in method 1.
6. Further discussion
6.1 Another method of universal hashing
Here is another method of constructing universal hash functions, which is slightly more efficient than the matrix method described earlier.
In the matrix method, we considered the key as a vector of bits. In this method, we will instead consider the key x as a vector of integers [x1, x2, ..., xk] with the only requirement that each xi be in the range {0, 1, ..., M-1}. For example, if we hash strings of length k, then xi can be the ith character (if the size of our table is at least 256) or the ith pair of characters (if the size of our table is at least 65536). In addition, we will require that the size of our table M be a prime. To select the hash function h, we select k random numbers r1, r2, ..., pk from {0, 1, ..., M - 1} and determine:
The proof that this method is universal is constructed in the same way as the proof of the matrix method. Let x and y be two different keys. We want to show that Prh (h (x) = h (y)) ≤ 1 / M. Since x! = Y, there must be a case when there exists some index i such that xi! = Yi. Now imagine that you first selected all the random numbers rj for j! = I. Let h ′ (x) = Pj6 = i rjxj. So, choosing ri, we get h (x) = h ′ (x) + rixi. This means that we have a conflict between x and y exactly when
Since M is prime, dividing by a nonzero value of mod M is valid (every integer from 1 to M −1 has a multiplicative inverse modulo M), which means that there is exactly one value ri modulo M for which the above equation holds true, namely ri = (h ′ (y) - h ′ (x)) / (xi - yi) mod M. Thus, the probability of this occurrence is exactly 1 / M.
6.2 Other uses of hashing
Suppose we have a long a sequence of elements, and we want to see how many different elements are in the list. Is there a good way to do this?
One way is to create a hash table, and then make one pass through the sequence by doing a search for each element and then inserting if it is not already in the table. The number of individual elements is simply the number of inserts.
And now, what if the list is really huge and we don’t have a place to store it, but an approximate answer is suitable for us. For example, imagine that we are a router and observe how many packets pass, and we want to (approximately) see how many different source IP addresses exist.
Here is a good idea: let's say we have a hash function h that behaves like a random function, and let's imagine that h (x) is a real number from 0 to 1. One thing we can do is just keep track of the minimum the hash value has been produced so far (so we won’t have a table at all). For example, if the keys are 3,10,3,3,12,10,12 and h (3) = 0.4, h (10) = 0.2, h (12) = 0.7, then we get 0, 2.
The fact is that if we select N random numbers in [0, 1], the expected minimum value will be 1 / (N + 1). In addition, there is a good chance that it is pretty close (we can improve our estimate by running several hash functions and taking the median of the lows).
Question: why use a hash function, and not just pick a random number every time? This is because we care about the number of different elements, and not just the total number of elements (this problem is much simpler: just use a counter ...).
Friends, was this article helpful to you? Write in the comments and join the open day , which will be held on April 25th.

1. Overview
Hashing is an excellent practical tool, with an interesting and subtle theory. In addition to using data as a vocabulary structure, hashing is also found in many different areas, including cryptography and complexity theory. In this lecture, we describe two important concepts: universal hashing (also known as universal family of hash functions) and ideal hashing.
The material highlighted in this lecture includes:
- The formal setting and the general idea of hashing.
- Universal hashing.
- Perfect hashing.
2. Introduction
We will consider the main problem with the dictionary, which we discussed before, and consider two versions: static and dynamic:
- Static : given a lot of S elements, we want to store it in such a way that we can quickly perform a search.
- For example, a fixed dictionary.
- Dynamic : here we have a sequence of requests for insertion, search, and possibly removal. We want to do all this effectively.
For the first problem, we could use a sorted array and a binary search. For the second, we could use a balanced search tree. However, hashing provides an alternative approach, which is often the fastest and most convenient way to solve these problems. For example, suppose you are writing a program for AI search and want to store situations that you have already resolved (positions on the board or elements of the state space) so as not to repeat the same calculations when you run into them again. Hashing provides an easy way to store this information. There are also many applications in cryptography, networks, complexity theory.
3. The basics of hashing The
formal formulation for hashing is as follows.
- The keys belong to some large set of U. (For example, imagine that U is a collection of all strings with a maximum length of 80 ascii characters.)
- There are some S keys in U that we really need (keys can be either static or dynamic). Let N = | S |. Imagine that N is much smaller than the size of U. For example, S is the set of student names in a class that is much smaller than 128 ^ 80.
- We will perform inserts and searches using an array A of some size M and a hash function h: U → {0, ..., M - 1}. Given element x, the idea of hashing is that we want to store it in A [h (x)]. Note that if U were small (for example, 2-character strings), then you could just save x in A [x], as in block sorting. The problem is that U is big, so we need a hash function.
- We need a method to resolve collisions. A collision is when h (x) = h (y) for two different keys x and y. In this lecture, we will handle collisions by defining each element of A as a linked list. There are a number of other methods, but for the problems that we will focus on here, this is the most suitable. This method is called the chaining method. To insert an item, we simply put it at the top of the list. If h is a good hash function, then we hope the lists will be small.
One of the great things about hashing is that all dictionary operations are incredibly easy to implement. To search for the key x, simply calculate the index i = h (x) and then go through the list in A [i] until you find it (or exit the list). To insert, simply place a new item at the top of its list. To delete, you just need to perform the delete operation in the linked list. Now we turn to the question: what do we need to achieve good performance?
Desirable properties. Key desirable properties for a good hash scheme:
- The keys are well dispersed so that we don’t have too many collisions, since collisions affect the search and deletion time.
- M = O (N): in particular, we would like our circuit to achieve property (1) without the need for the size of table M to be much larger than the number of elements N.
- The function h must be calculated quickly. In our analysis today, we will consider the time to calculate h (x) as a constant. However, it is worth remembering that it should not be too complicated because it affects the overall execution time.
Given this, the search time for the element x is O (the size of the list is A [h (x)]). The same is true for deletions. Insertions take O (1) time regardless of the length of the lists. So, we want to analyze how big these lists are.
Basic intuition: one way to distribute elements beautifully is to distribute them randomly. Unfortunately, we cannot just use the random number generator to decide where to direct the next element, because then we can never find it again. So, we want h to be something “pseudo-random” in some formal sense.
Now we will present some bad news, and then some good news.
Statement 1 (Bad News) For any hash function h if | U | ≥ (N −1) M +1, there is a set S of N elements that all hashed in one place.
Proof: by the Dirichlet principle. In particular, to consider counterpoints, if each location had no more than N - 1 elements of U that hash it, then U could have a size of no more than M (N - 1).
This is partly why hashing seems so mysterious - how can it be argued that hashing is good if for any hash function you can think of ways to prevent it? One answer is that there are many simple hash functions that work well in practice for typical S sets. But what if we want a good guarantee of the worst case?
Here's the key idea: let's use randomization in our h construct, similar to randomized quicksort. (Needless to say, h will be a deterministic function). We will show that for any sequence of insertion and search operations (we do not need to assume that the set of inserted elements S is random), if we choose h in this probabilistic way, the performance of h in this sequence will be good in anticipation. Thus, this is the same guarantee as in randomized quicksort or traps. In particular, this is the idea of universal hashing.
Once we develop this idea, we will use it for a particularly enjoyable application called “perfect hashing”.
4. Universal hashing
Definition 1. The randomized algorithm H for constructing the hash functions h: U → {1, ..., M} is
universal if for all x! = Y in U we have

We can also say that the set H of hash functions is a universal hash family functions if the procedure “choose h ∈ H at random” is universal. (Here we identify the set of functions with a uniform distribution over the set.)
Theorem 2. If H is universal, then for any set S ⊆ U of size N, for any x ∈ U (for example, which we could look for), if we construct h randomly Thus, in accordance with H, the expected number of collisions between x and other elements in S is no more than N / M.
Proof: each y ∈ S (y! = X) has at most 1 / M chance of a collision with x by the definition of “universal”. So,
- Let Cxy = 1 if x and y collide, and 0 otherwise.
- Let Cx denote the total number of collisions for x. So, Cx = Py∈S, y! = X Cxy.
- We know that E [Cxy] = Pr (x and y collide) ≤ 1 / M.
- Thus, in linearity of expectation, E [Cx] = Py E [Cxy]
Now we get the following corollary.
Corollary 3. If H is universal, then for any sequence of insertion, search, and deletion operations L, in which there can be no more than M elements in a system at a time, the expected total cost of L operations for a random h ∈ H is only O (L) (viewing the time to calculate h as constants).
Proof: for any given operation in the sequence, its expected cost is constant by Theorem 2, so the expected total cost of L operations is O (L) in linearity of expectation.
Question: can we actually build a universal H? If not, then this is all pretty pointless. Fortunately, the answer is yes.
4.1. Creating a universal hash family: matrix method
Suppose the keys are u-bits long. Say, the size of table M is equal to degree 2; therefore, the index is b-bit long with M = 2b.
What we will do is choose h as the random matrix 0/1 b-by-u and define h (x) = hx, where we add mod 2. These matrices are short and thick. For example:

Proposition 4. For x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.
Proof: First, what does multiplying h by x mean? We can think of it as adding some of the columns h (doing vector addition mod 2), where 1 bit in x indicates which ones to add. (for example, we added the 1st and 3rd columns of h above)
Now take an arbitrary key pair x, y such that x! = Y. They should be different somewhere, so, say, they differ in the i-th coordinate, and for concreteness we say xi = 0 and yi = 1. Imagine that we first selected all h except the i-th column. For the remaining samples of the ith column, h (x) is fixed. However, each of 2b different settings of the ith column gives a different value of h (y) (in particular, every time we turn a bit in this column, we turn the corresponding bit into h (y)). So there is exactly a 1 / 2b chance that h (x) = h (y).
There are other methods for constructing universal hash families, which are also based on the multiplication of primes (see Section 6.1).
The next question that we will consider: if we correct the set S, can we find a hash function h such that all searches will have constant time? The answer is yes, and this leads to the topic of perfect hashing.
5. Perfect Hashing
We say that a hash function is ideal for S if all searches occur in O (1). Here are two ways to build ideal hash functions for a given set S.
5.1 Method 1: a solution in O (N2) space
Let's say we want to have a table whose size is quadratic in size N of our dictionary S. Then here is a simple method for constructing an ideal hash function . Let H be universal and M = N2. Then just pick a random h from H and try it! The statement is that there is at least a 50% chance that she will not have collisions.
Proposition 5. If H is universal and M = N2, then Prh∼H (no collisions in S) ≥ 1/2.
Proof:
• How many pairs (x, y) are there in S? Answer:

• For each pair, the probability of their collision is ≤ 1 / M by definition of universality.
• So Pr (there is a collision) ≤
 / M <1/2.
/ M <1/2. This is like the other side of the "birthday paradox." If the number of days is much larger than the number of people squared, then there is a reasonable chance that no couple will have the same birthday.
So, we just pick a random h from H, and if any collisions arise, we just pick a new h. On average, we will only need to do this twice. Now, what if we want to use only the O (N) space?
5.2 Method 2: a solution in the space O (N)
The question of whether it is possible to achieve perfect hashing in O (N) space has been open for some time: "Should the tables be sorted?" That is, for a fixed set, you can get a constant search time only with linear space? There was a series of more and more complex attempts, until finally it was solved using the good idea of universal hash functions in a two-level scheme.
The method is as follows. First, we will hash into a table of size N using universal hashing. This will lead to some collisions (unless we are lucky). However, then we rehash each basket using method 1, squaring the basket size to get zero collisions. Thus, the scheme consists in the fact that we have a hash function of the first level h and a table A of the first level, and then N hash functions of the second level h1, ..., hN and N of the second level table A1, ..., A.N ... To find the element x, we first compute i = h (x), and then find the element in Ai [hi (x)]. (If you did this in practice, you could set the flag so that you would take the second step only if there really were conflicts with the index i, otherwise you would just put x itself in A [i], but let's let's not worry about it here.)
Say a hash function h hashes n elements of S to location i. We have already proved (by analyzing method 1) that we can find h1, ..., hN, so that the total space used in the secondary tables is Pi (ni) 2. It remains to show that we can find a first-level function h such that Pi (ni) 2 = O (N). In fact, we show the following:
Theorem 6. If we choose the starting point h from the universal set H, then
Pr[X
i
(ni)2 > 4N] < 1/2.Evidence. Let us prove this by showing that E [Pi (ni) 2] <2N. This implies what we want from Markov inequality. (If there were a probability of even 1/2 that the amount could be more than 4N, this fact alone would mean that the expectation should be more than 2N. Thus, if the expectation is less than 2N, the probability of failure should be less 1/2.)
Now, the tricky trick is that one way to calculate this amount is to count the number of ordered pairs that have a collision, including collisions with oneself. For example, if the basket has {d, e, f}, then d will have a conflict with each of {d, e, f}, e will have a conflict with each of {d, e, f}, and f will have a conflict with each of {d, e, f}, so we get 9. So, we have:
E[X
i
(ni)2] = E[X
x
X
y
Cxy] (Cxy = 1 if x and y collide, else Cxy = 0)
= N +X
x
X
y6=x
E[Cxy]
≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal)
< 2N. (since M = N)
So, we just try a random h from H until we find one such that Pi n2 i <4N, and then fixing this function h, we find N secondary hash functions h1, ..., hN as in method 1.
6. Further discussion
6.1 Another method of universal hashing
Here is another method of constructing universal hash functions, which is slightly more efficient than the matrix method described earlier.
In the matrix method, we considered the key as a vector of bits. In this method, we will instead consider the key x as a vector of integers [x1, x2, ..., xk] with the only requirement that each xi be in the range {0, 1, ..., M-1}. For example, if we hash strings of length k, then xi can be the ith character (if the size of our table is at least 256) or the ith pair of characters (if the size of our table is at least 65536). In addition, we will require that the size of our table M be a prime. To select the hash function h, we select k random numbers r1, r2, ..., pk from {0, 1, ..., M - 1} and determine:
h(x) = r1x1 + r2x2 + . . . + rkxk mod M.The proof that this method is universal is constructed in the same way as the proof of the matrix method. Let x and y be two different keys. We want to show that Prh (h (x) = h (y)) ≤ 1 / M. Since x! = Y, there must be a case when there exists some index i such that xi! = Yi. Now imagine that you first selected all the random numbers rj for j! = I. Let h ′ (x) = Pj6 = i rjxj. So, choosing ri, we get h (x) = h ′ (x) + rixi. This means that we have a conflict between x and y exactly when
h′(x) + rixi = h′(y) + riyi mod M, or equivalently when
ri(xi − yi) = h′(y) − h′(x) mod M.Since M is prime, dividing by a nonzero value of mod M is valid (every integer from 1 to M −1 has a multiplicative inverse modulo M), which means that there is exactly one value ri modulo M for which the above equation holds true, namely ri = (h ′ (y) - h ′ (x)) / (xi - yi) mod M. Thus, the probability of this occurrence is exactly 1 / M.
6.2 Other uses of hashing
Suppose we have a long a sequence of elements, and we want to see how many different elements are in the list. Is there a good way to do this?
One way is to create a hash table, and then make one pass through the sequence by doing a search for each element and then inserting if it is not already in the table. The number of individual elements is simply the number of inserts.
And now, what if the list is really huge and we don’t have a place to store it, but an approximate answer is suitable for us. For example, imagine that we are a router and observe how many packets pass, and we want to (approximately) see how many different source IP addresses exist.
Here is a good idea: let's say we have a hash function h that behaves like a random function, and let's imagine that h (x) is a real number from 0 to 1. One thing we can do is just keep track of the minimum the hash value has been produced so far (so we won’t have a table at all). For example, if the keys are 3,10,3,3,12,10,12 and h (3) = 0.4, h (10) = 0.2, h (12) = 0.7, then we get 0, 2.
The fact is that if we select N random numbers in [0, 1], the expected minimum value will be 1 / (N + 1). In addition, there is a good chance that it is pretty close (we can improve our estimate by running several hash functions and taking the median of the lows).
Question: why use a hash function, and not just pick a random number every time? This is because we care about the number of different elements, and not just the total number of elements (this problem is much simpler: just use a counter ...).
Friends, was this article helpful to you? Write in the comments and join the open day , which will be held on April 25th.
