Delaunay triangulation algorithm by sweeping line method

Good day!

In this article, I will describe in detail the algorithm that I obtained as a result of using the idea of ​​“sweeping the straight line” to construct the Delaunay triangulation on a plane. There are several ideas in it that I never met when I read articles about triangulation.
Perhaps someone will also find them unusual. I will try to do everything in the best tradition and include the following things in the story: a description of the data structures used, a description of the steps of the algorithm, proof of correctness, time estimates, as well as a comparison with an iterative algorithm using the kD tree.

Definitions and statement of the problem

Triangulation

It is said that triangulation is given on the set of points on the plane if some pairs of points are connected by an edge, any finite face in the resulting graph forms a triangle, the edges do not intersect, and the graph is maximal in the number of edges.

Delaunay Triangulation

A Delaunay triangulation is a triangulation in which for any triangle it is true that there are no points from the original set inside the circle circumscribed around it.

Note : for a given set of points in which no 4 points are on the same circle, there is exactly one Delaunay triangulation.

The Delaunay Condition

Let a triangulation be given on the set of points. We say that a certain subset of points satisfies the Delaunay condition if the triangulation bounded on this subset is the Delaunay triangulation for him.

Criterion for Delaunay Triangulation

The fulfillment of the Delaunay condition for all points forming a quadrangle in a triangulation is equivalent to the fact that this triangulation is a Delaunay triangulation.

Note : for non-convex quadrangles, the Delaunay condition is always fulfilled, and for convex quadrangles (whose vertices do not lie on the same circle) there are exactly 2 possible triangulations (one of which is the Delaunay triangulation).

The task is to construct a Delaunay triangulation for a given set of points.

Algorithm description

Visible points and visible edges

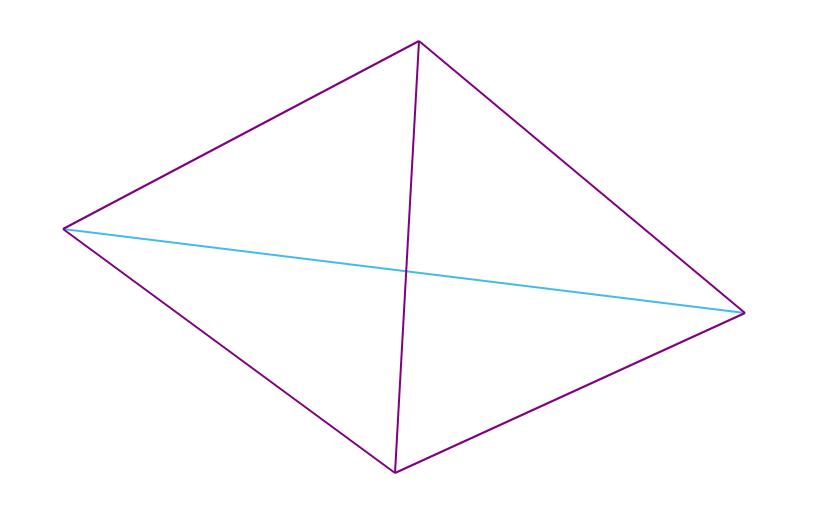
Let a minimal convex hull (hereinafter, MBO) be given of a finite set of points (edges connecting some of the points so that they form a polygon containing all points of the set) and a point A lying outside the hull. Then the point of the plane is called visible for point A, if the segment connecting it to point A does not intersect the MBO.

An MBO edge is called visible for point A if its ends are visible for A.

In the next picture, the edges visible for the red point are marked in red:

Note : the Delaunay triangulation contour is the MBO for the points on which it is built.

Remark 2 : in the algorithm, the edges visible for the added point A form a chain, that is, several MBO edges in a row

Storing triangulation in memory

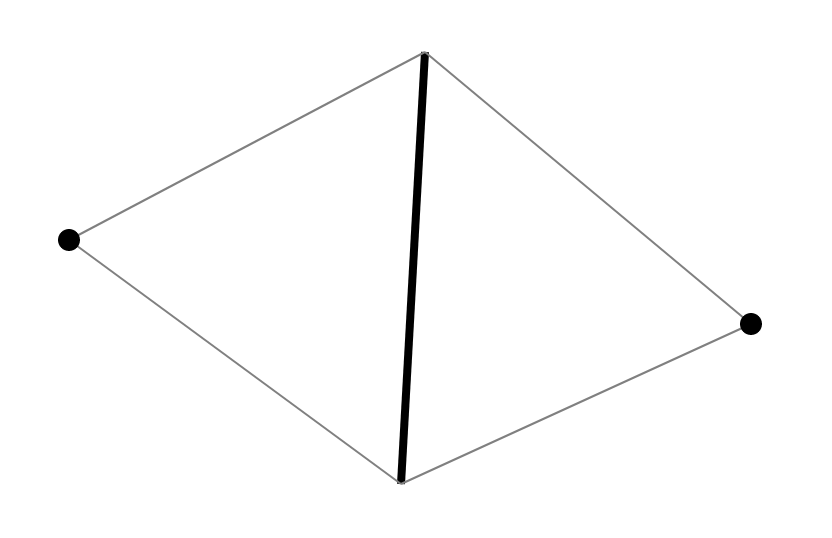
There are some standard methods that are well described in the book of Skvortsov [1]. Due to the specifics of the algorithm, I will offer my own version. Since we want to check the 4-gons for the Delaunay condition, we consider their structure. Each quadrangle in triangulation is 2 triangles having a common edge. Each edge has exactly 2 triangles adjacent to it. Thus, each quadrangle in triangulation is generated by an edge and two vertices opposite the edge in adjacent triangles.
Since two triangles and their adjacency are restored along the edge and two vertices, we can restore triangulation for all such structures. Accordingly, it is proposed to store an edge with two vertices in the set and perform a search along the edge (an ordered pair of vertices).

Algorithm

The idea of ​​the sweeping line is that all points are sorted in one direction, and then processed in turn.

1. Sort all points along a straight line (for simplicity, by coordinate $$)
2. We construct a triangle on the first 3 points.
   
   Further, for each next point we will carry out steps that preserve the invariant that there is a Delaunay triangulation for points already added and, accordingly, an MBO for them.
3. Add the triangles formed by the visible edges and the point itself (that is, add the edges from the point in question to all ends of the visible edges).
4. We check on the Delaunay condition all the quadrangles generated by the visible edges. If the condition is not fulfilled somewhere, then we rebuild the triangulation in the quadrangle (I recall that there are only two of them) and recursively run the check for the quadrangles generated by the edges of the current quadrangle (because only after them the Delaunay condition could be violated).

Note : in step (4) during a recursive start, you can not check the quadrangles generated by the edges coming from the point considered at this iteration (there are always two out of four of them). Most often they will be non-convex, for convex the proof is purely geometric, I will leave it to the reader. Further, we assume that only 2 recursive starts are performed for each rebuild.

Verifying a Delaunay Condition

Ways to test quadrangles for the Delaunay condition can be found in the same book [1]. I only note that when choosing a method with trigonometric functions from there, with inaccurate implementation, negative values ​​of sines can be obtained, it makes sense to take them modulo.

Search for visible edges

It remains to understand how to effectively find visible edges. Note that the previous added point S is in the MBO at the current iteration, since it has the largest coordinate$$, and is also visible for the current point. Then, noting that the ends of the visible edges form a continuous chain of visible points, we can go from point S in both directions along the MBO and collect the edges while they are visible (the visibility of the edge is checked using the vector product). Thus, it is convenient to store the MBO as a doubly connected list, at each iteration removing visible edges and adding 2 new ones from the considered point.

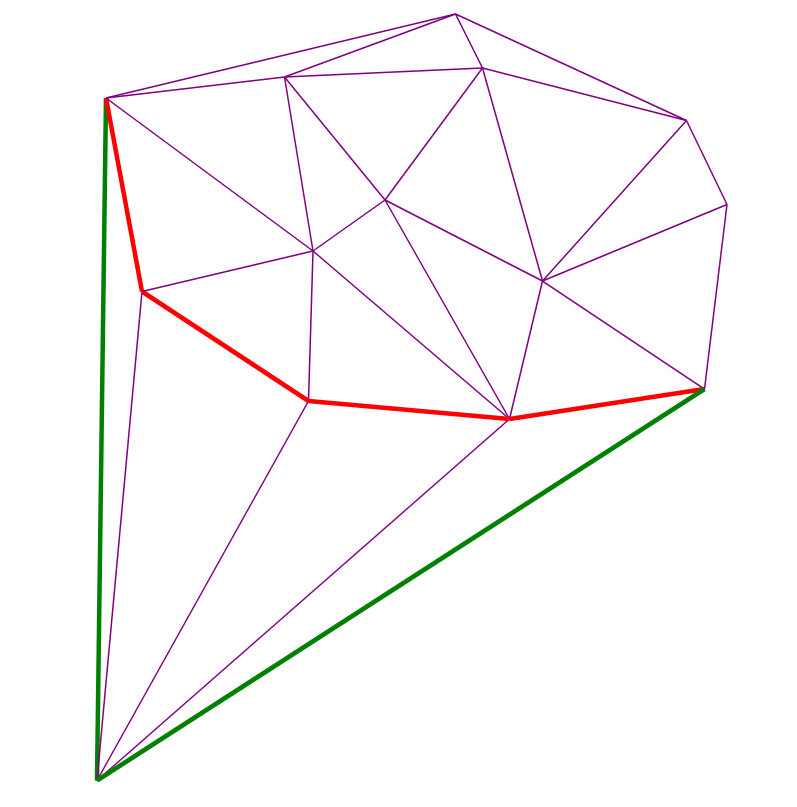
Algorithm visualization

Two red dots - added and previous. Red edges at each moment make up the recursion stack from step (4):

Algorithm correctness

To prove the correctness of the algorithm, it is enough to prove the conservation of the invariant in steps (3) and (4).

Step (3)

After step (3), obviously, we get some triangulation of the current set of points.

Step (4)

In the process of step (4), all the quadrangles that do not satisfy the Delaunay condition are in the recursion stack (follows from the description), which means that at the end of step (4) all the quadrangles satisfy the Delaunay condition, that is, the Delaunay triangulation is actually constructed. Then it remains to prove that the process in step (4) will someday end. This follows from the fact that all edges added during the rebuild come from the current vertex in question (i.e., in step$$ there are no more than $$) and from the fact that after adding these edges we will not consider the quadrangles generated by them (see the previous remark), which means we will add no more than once.

Time complexity

On average, the algorithm works pretty well on uniform, normal distributions (the results are shown in the table below). There is an assumption that its working time is$$. In the worst case, an assessment takes place$$.

Let’s take a look at the working time in parts and understand which one has the greatest impact on the total time:

Sort by direction

For sorting, we will use the estimate $$.

Search for visible edges

First, we show that the total time spent searching for visible edges is $$. Note that at each iteration we find all visible edges and 2 more (first not visible) in linear time. In step (3), we add new 2 edges to the MBO. Thus, in total, no more than$$ ribs, therefore, and various visible ribs will be no more $$. We will also find$$edges that are not visible. Thus, in total there is no more$$ ribs that corresponds to time $$.

Building new triangles

The total time for constructing triangles from step (3) with visible edges already found is obviously $$.

Rebuilding triangulation

It remains to deal with step (4). First, note that checking the Delaunay condition and rebuilding if it is not fulfilled are quite expensive actions (although they work for$$) Only on checking the Delaunay condition can take about 28 arithmetic operations. Let's look at the average number of rebuilds during this step. Practical results on some distributions are given below. For them I really want to say that the average number of rearrangements grows with a logarithmic speed, but let us leave this as an assumption.

Here I also want to note that the average number of rearrangements per point can vary greatly from the direction along which sorting is performed. So for a million evenly distributed on a long low rectangle with an aspect ratio of 100000: 1, this number varies from 1.2 to 24 (these values ​​are achieved when sorting data horizontally and vertically, respectively). Therefore, I see the point in choosing the sort direction in an arbitrary way (in this example, with arbitrary selection, on average about 2 rebuilds were obtained) or manually select it if the data is known in advance.

Thus, the main time the program usually takes to step (4). If it runs quickly, it makes sense to think about speeding up sorting.

Worst case

Worst case on $$th iteration occurs $$ the recursive call in step (4), i.e., summing over all i, we obtain the asymptotic behavior in the worst case $$. The following picture illustrates a beautiful example on which the program can work for a long time (1100 rebuilds on average when adding a new point with an input of 10,000 points).

Comparison with an iterative algorithm for constructing a Delaunay triangulation using kD-tree

Description of the iterative algorithm

I will briefly describe the above algorithm. When the next point arrives, we use the kD-tree (I advise you to read about it somewhere, if you do not know), we find a triangle that is already quite close to it. Then bypassing in depth we look for a triangle, into which the point itself falls. We extend the edges to the vertices of the found triangle and actually perform step (4) from our algorithm for the new quadrangles. Since the point can be outside the triangulation, for simplification it is proposed to cover all points with a large triangle (to construct it in advance), this will solve the problem.

Similarity of algorithms

In fact, if points are added in order sorted by direction, then our algorithm actually works the same as iterative, except that the number of rearrangements is less. The following animation demonstrates this perfectly. On it, points were added from right to left, and they are all covered by a large triangle, which is subsequently removed.

Algorithm Differences

In an iterative algorithm, the localization of a point (search for the desired triangle) occurs on average over $$, on the above distributions, on average, 3 rearrangements occur (as shown in [1]) under the condition of an arbitrary order of supply of points. Thus, the sweeping line wins the time of the iterative algorithm in localization, but loses it in rebuilding (which, I recall, are quite difficult). In addition, the iterative algorithm works online, which is also its distinguishing feature.

Conclusion

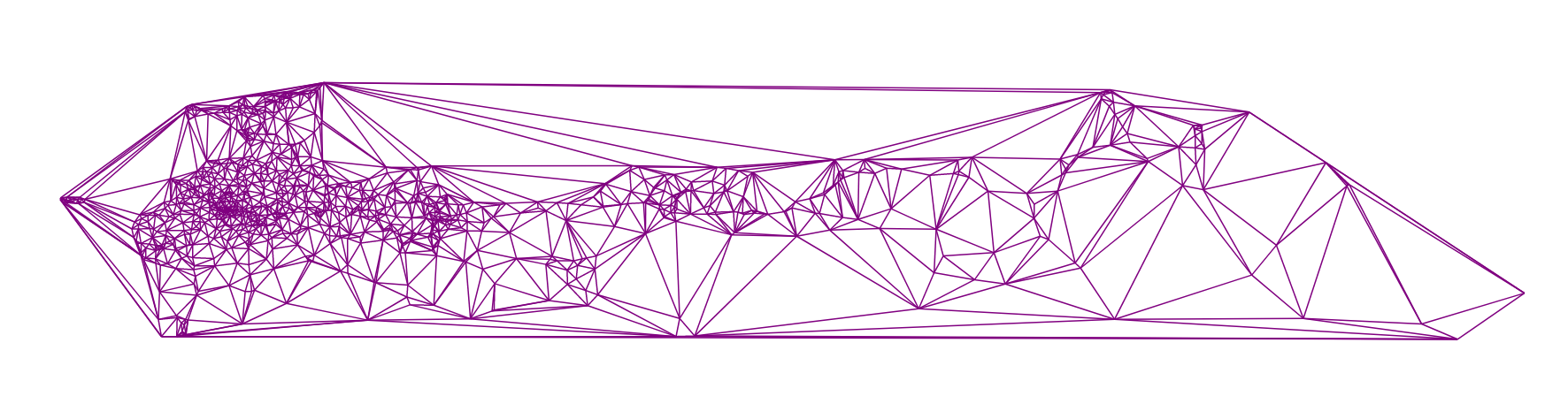
Here I just show some interesting triangulations resulting from the operation of the algorithm.

Beautiful pattern

Normal distribution, 1000 points

Even distribution, 1000 points

Triangulation built on the locations of all cities of Russia

Here you can see an example of my code for this algorithm:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

Thank you for your attention!

Literature

[1] Skvortsov A.V. Delaunay triangulation and its application. - Tomsk: Publishing house Tom. University, 2002 .-- 128 p. ISBN 5-7511-1501-5