Data Science: predicting business events to improve service
Algorithms for recommendations, predictions of events or risk assessments are a trend decision in banks, insurance companies and many other business sectors. For example, these programs help, based on data analysis, to suggest when a client will return a bank loan, what will be the demand in retail, what is the probability of an insured event or an outflow of customers in telecom, etc. For a business, this is a valuable opportunity to optimize their expenses, increase the speed of work, and generally improve the service.
However, traditional approaches such as classification and regression are not suitable for building such programs. Consider this problem as an example of a case predicting medical episodes: we analyze the nuances in the nature of data and possible approaches to modeling, build a model and analyze its quality.
The prediction of episodes is based on an analysis of historical data. The dataset in this case consists of two parts. The first is data on services previously provided to the patient. This part of the dataset includes socio-demographic data about the patient, such as age and gender, as well as diagnoses made to him at different times in the ICD10-CM encoding [1] and HCPCS procedures performed [2]. These data form sequences in time that allow you to get an idea of the patient’s condition at a particular moment. For training models, as well as for working in production, personalized data is enough.
The second part of the dataset is a list of episodes that occur for the patient. For each episode we indicate its type and date of occurrence, as well as the time period, included services and other information. From these data, target variables for prediction are generated.
The aspect of time is important in the problem being solved: we are only interested in episodes that may arise in the near future. On the other hand, the dataset at our disposal was collected for a limited period of time, beyond which there is no data. Thus, we cannot say whether episodes occur outside the observation period, what episodes are they, at what exact moment in time they arise. This situation is called right censoring.
Similarly, left censoring occurs: for some patients, an episode may begin to develop earlier than is available to our observation. For us, it will look like an episode that arose without any background.
There is another type of censorship of data - interruption of observation (if the observation period is not completed and the event has not occurred). For example, due to a patient moving, a failure in the data collection system, and so on.
In fig. 1 schematically shows different types of censorship of data. All of them distort statistics and make building a model difficult.
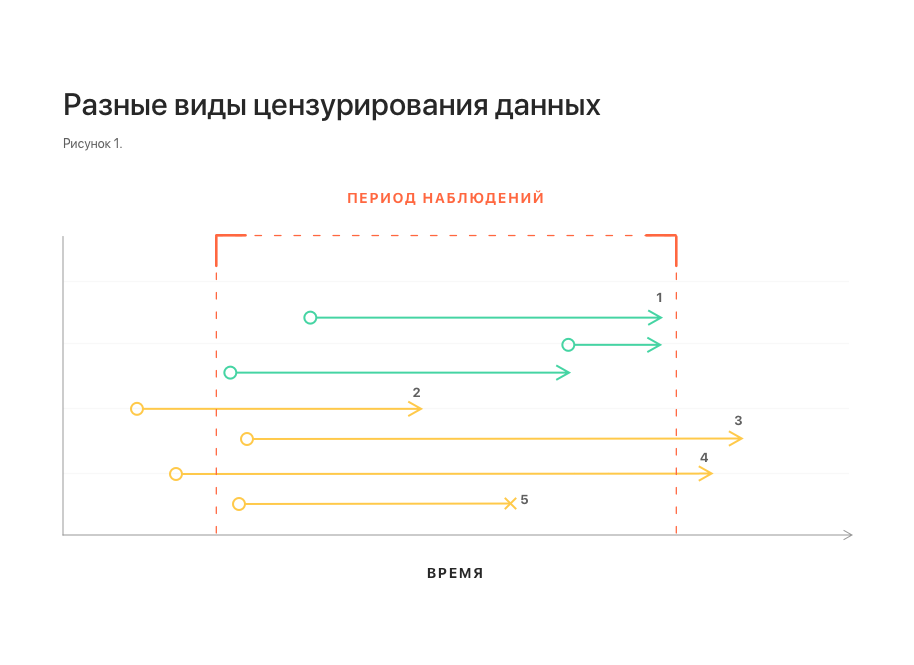
Notes: 1 - uncensored observations; 2, 3 - left and right censorship, respectively; 4 - left and right censorship at the same time;
5 - interruption of observation.
Another important feature of the dataset is related to the nature of the data stream in real life. Some data may arrive late, in which case they are not available at the time of the prediction. To take this feature into account, it is necessary to supplement the dataset by throwing several elements from the tail of each sequence.
Naturally, the first thought will be to reduce the problem to the well-known classification and regression. However, these approaches encounter serious difficulties.
Why regression does not suit us, it is clear from the considered phenomena of right and left censorship: the distribution of the time of occurrence of an episode in the dataset can be shifted. Moreover, the magnitude and the fact of the presence of this bias cannot be determined using the dataset itself. The constructed model can show arbitrarily good results with any approaches to validation, but this, most likely, will have nothing to do with its suitability for forecasting on production data.
More promising, at first glance, is an attempt to reduce the problem to classification: to set a certain period of time and determine the episode that will arise in this period. The main difficulty here is the binding of the time interval of interest to us. It can be reliably linked only to the moment of the last update of the patient’s history. At the same time, the request to predict the episode is generally not tied to time and can come at any moment, both inside this period (and then the effective period of interest is shortened), and completely beyond it - and then the prediction generally loses its meaning (see Fig. 2). This naturally induces an increase in the period of interest, which ultimately reduces the value of the prediction anyway.

Notes: 1 - updates the patient's history; 2 - the latest update and the time span associated with it; 3, 4 - episode prediction requests received during this period. It is seen that the effective prediction interval for them is less; 5 - request received outside the interval. For him, prediction is impossible.
As an alternative, we can consider the approach, in Russian literature called survival analysis (survival analysis, or time-to-event analysis) [3]. This is a family of models designed specifically for working with censored data. It is based on the approximation of the risk function (hazard function, intensity of occurrence of events), which estimates the probability distribution of the occurrence of an event over time. This approach allows you to correctly take into account the presence of different types of censorship.
For the problem being solved, this approach additionally allows combining both aspects of the problem in one model: determining the type of episode and predicting the time of its occurrence. To do this, it is enough to build a separate model for each type of episode, similar to the one-vs-all approach in the classification. Then the occurrence of a non-target episode can be interpreted as the exclusion of an object from the observed sample without the occurrence of an event, which is another type of censorship of data and is also correctly taken into account by the model. This interpretation is correct from the point of view of business logic: if a patient has cataract surgery, this does not exclude the occurrence of other episodes for him in the future.
Among the family of models for survival analysis, two varieties can be distinguished: analytical and regression. Analytical models are purely descriptive, they are built for the whole population, do not take into account the features of its individual members, and therefore can only predict the occurrence of an event for some typical member of the population. Unlike analytical, regression models are built taking into account the characteristics of individual members of the population and allow forecasts to be made also for individual members taking into account their characteristics. in this problem, it was this variation that was used, or rather, the Cox's Proportional Hazard model (hereinafter - CoxPH).
The simplest approach will be similar to conventional regression: take the mathematical expectation of the time of the onset of the event as the output. Since CoxPH receives data as a numerical vector at the input, and our dataset is, in fact, a sequence of diagnosis codes and procedures (categorical data), preliminary data transformation is required:
We use the obtained feature vectors for model training and its validation. The resulting model demonstrates the following concordance index (c-index or c-statistic) values [5]:
This is comparable to the level of 0.6–0.7 usual for such models [6].
However, if you look at the mean absolute error between the predicted expected time of occurrence of the episode and the actual one, it turns out that the error is 5 days. The reason for such a big mistake is that optimization for c-index guarantees only the correct order of values: if one event should occur earlier than another, then the predicted values of the expected time to events will be one less than the other, respectively. Moreover, no statements are made regarding the predicted values themselves.
Another possible variant of the output value of the model is a table of values of the risk function at different points in time. This option has a more complex structure, it is more difficult to interpret than the previous one, but at the same time it provides more information.
Changing the output format requires a different way of assessing the quality of the model: we need to make sure that for positive examples (when an episode occurs) the risk level is higher than for negative examples (when an episode does not occur). To do this, for each predicted distribution of the risk function in the delayed sample, we will move from the table of values to one value - the maximum. Having counted the median values for positive and negative examples, we will see that they reliably differ: 0.13 versus 0.04, respectively.
Next, we use these values to build the ROC curve and calculate the area under it - ROC AUC, which is 0.92, which is acceptable for the problem being solved.
Thus, we saw that the survival analysis is the best approach for solving the problem of predicting medical episodes, taking into account all the nuances of the problem and the available data. However, its application implies a different format of the model output data and a different approach to assessing its quality.
Applying the CoxPH model to predicting episodes of cataract surgery allowed us to achieve acceptable model quality indicators. A similar approach can be applied to other types of episodes, but specific quality indicators of models can only be evaluated directly in the modeling process.
[1] ICD-10 Clinical Modification en.wikipedia.org/wiki/ICD-10_Clinical_Modification
[2] Healthcare Common Procedure Coding System en.wikipedia.org/wiki/Healthcare_Common_Procedure_Coding_System
[3] Survival analysis en.wikipedia.org/wiki/Survival_anysis
[4] GloVe: Global Vectors for Word Representation nlp.stanford.edu/projects/glove
[5] C-Statistic: Definition, Examples, Weighting and Significance www.statisticshowto.datasciencecentral.com/c-statistic
[6] VC Raykar et al. On Ranking in Survival Analysis: Bounds on the Concordance Index papers.nips.cc/paper/3375-on-ranking-in-survival-analysis-bounds-on-the-concordance-index.pdf
However, traditional approaches such as classification and regression are not suitable for building such programs. Consider this problem as an example of a case predicting medical episodes: we analyze the nuances in the nature of data and possible approaches to modeling, build a model and analyze its quality.
The challenge of predicting medical episodes
The prediction of episodes is based on an analysis of historical data. The dataset in this case consists of two parts. The first is data on services previously provided to the patient. This part of the dataset includes socio-demographic data about the patient, such as age and gender, as well as diagnoses made to him at different times in the ICD10-CM encoding [1] and HCPCS procedures performed [2]. These data form sequences in time that allow you to get an idea of the patient’s condition at a particular moment. For training models, as well as for working in production, personalized data is enough.
The second part of the dataset is a list of episodes that occur for the patient. For each episode we indicate its type and date of occurrence, as well as the time period, included services and other information. From these data, target variables for prediction are generated.
The aspect of time is important in the problem being solved: we are only interested in episodes that may arise in the near future. On the other hand, the dataset at our disposal was collected for a limited period of time, beyond which there is no data. Thus, we cannot say whether episodes occur outside the observation period, what episodes are they, at what exact moment in time they arise. This situation is called right censoring.
Similarly, left censoring occurs: for some patients, an episode may begin to develop earlier than is available to our observation. For us, it will look like an episode that arose without any background.
There is another type of censorship of data - interruption of observation (if the observation period is not completed and the event has not occurred). For example, due to a patient moving, a failure in the data collection system, and so on.
In fig. 1 schematically shows different types of censorship of data. All of them distort statistics and make building a model difficult.

Notes: 1 - uncensored observations; 2, 3 - left and right censorship, respectively; 4 - left and right censorship at the same time;
5 - interruption of observation.
Another important feature of the dataset is related to the nature of the data stream in real life. Some data may arrive late, in which case they are not available at the time of the prediction. To take this feature into account, it is necessary to supplement the dataset by throwing several elements from the tail of each sequence.
Classification and Regression
Naturally, the first thought will be to reduce the problem to the well-known classification and regression. However, these approaches encounter serious difficulties.
Why regression does not suit us, it is clear from the considered phenomena of right and left censorship: the distribution of the time of occurrence of an episode in the dataset can be shifted. Moreover, the magnitude and the fact of the presence of this bias cannot be determined using the dataset itself. The constructed model can show arbitrarily good results with any approaches to validation, but this, most likely, will have nothing to do with its suitability for forecasting on production data.
More promising, at first glance, is an attempt to reduce the problem to classification: to set a certain period of time and determine the episode that will arise in this period. The main difficulty here is the binding of the time interval of interest to us. It can be reliably linked only to the moment of the last update of the patient’s history. At the same time, the request to predict the episode is generally not tied to time and can come at any moment, both inside this period (and then the effective period of interest is shortened), and completely beyond it - and then the prediction generally loses its meaning (see Fig. 2). This naturally induces an increase in the period of interest, which ultimately reduces the value of the prediction anyway.

Notes: 1 - updates the patient's history; 2 - the latest update and the time span associated with it; 3, 4 - episode prediction requests received during this period. It is seen that the effective prediction interval for them is less; 5 - request received outside the interval. For him, prediction is impossible.
Survival analysis
As an alternative, we can consider the approach, in Russian literature called survival analysis (survival analysis, or time-to-event analysis) [3]. This is a family of models designed specifically for working with censored data. It is based on the approximation of the risk function (hazard function, intensity of occurrence of events), which estimates the probability distribution of the occurrence of an event over time. This approach allows you to correctly take into account the presence of different types of censorship.
For the problem being solved, this approach additionally allows combining both aspects of the problem in one model: determining the type of episode and predicting the time of its occurrence. To do this, it is enough to build a separate model for each type of episode, similar to the one-vs-all approach in the classification. Then the occurrence of a non-target episode can be interpreted as the exclusion of an object from the observed sample without the occurrence of an event, which is another type of censorship of data and is also correctly taken into account by the model. This interpretation is correct from the point of view of business logic: if a patient has cataract surgery, this does not exclude the occurrence of other episodes for him in the future.
Among the family of models for survival analysis, two varieties can be distinguished: analytical and regression. Analytical models are purely descriptive, they are built for the whole population, do not take into account the features of its individual members, and therefore can only predict the occurrence of an event for some typical member of the population. Unlike analytical, regression models are built taking into account the characteristics of individual members of the population and allow forecasts to be made also for individual members taking into account their characteristics. in this problem, it was this variation that was used, or rather, the Cox's Proportional Hazard model (hereinafter - CoxPH).
Survival regression and cataract surgery
The simplest approach will be similar to conventional regression: take the mathematical expectation of the time of the onset of the event as the output. Since CoxPH receives data as a numerical vector at the input, and our dataset is, in fact, a sequence of diagnosis codes and procedures (categorical data), preliminary data transformation is required:
- Translation of codes into an embedded representation using the previously trained GloVe model [4];
- Aggregation of all codes available in the last period of the patient’s history into a single vector;
- One-hot coding of the patient’s gender and scaling of the age.
We use the obtained feature vectors for model training and its validation. The resulting model demonstrates the following concordance index (c-index or c-statistic) values [5]:
- 0.71 for 5-fold validation;
- 0.69 on the pending sample.
This is comparable to the level of 0.6–0.7 usual for such models [6].
However, if you look at the mean absolute error between the predicted expected time of occurrence of the episode and the actual one, it turns out that the error is 5 days. The reason for such a big mistake is that optimization for c-index guarantees only the correct order of values: if one event should occur earlier than another, then the predicted values of the expected time to events will be one less than the other, respectively. Moreover, no statements are made regarding the predicted values themselves.
Another possible variant of the output value of the model is a table of values of the risk function at different points in time. This option has a more complex structure, it is more difficult to interpret than the previous one, but at the same time it provides more information.
Changing the output format requires a different way of assessing the quality of the model: we need to make sure that for positive examples (when an episode occurs) the risk level is higher than for negative examples (when an episode does not occur). To do this, for each predicted distribution of the risk function in the delayed sample, we will move from the table of values to one value - the maximum. Having counted the median values for positive and negative examples, we will see that they reliably differ: 0.13 versus 0.04, respectively.
Next, we use these values to build the ROC curve and calculate the area under it - ROC AUC, which is 0.92, which is acceptable for the problem being solved.
Conclusion
Thus, we saw that the survival analysis is the best approach for solving the problem of predicting medical episodes, taking into account all the nuances of the problem and the available data. However, its application implies a different format of the model output data and a different approach to assessing its quality.
Applying the CoxPH model to predicting episodes of cataract surgery allowed us to achieve acceptable model quality indicators. A similar approach can be applied to other types of episodes, but specific quality indicators of models can only be evaluated directly in the modeling process.
Literature
[1] ICD-10 Clinical Modification en.wikipedia.org/wiki/ICD-10_Clinical_Modification
[2] Healthcare Common Procedure Coding System en.wikipedia.org/wiki/Healthcare_Common_Procedure_Coding_System
[3] Survival analysis en.wikipedia.org/wiki/Survival_anysis
[4] GloVe: Global Vectors for Word Representation nlp.stanford.edu/projects/glove
[5] C-Statistic: Definition, Examples, Weighting and Significance www.statisticshowto.datasciencecentral.com/c-statistic
[6] VC Raykar et al. On Ranking in Survival Analysis: Bounds on the Concordance Index papers.nips.cc/paper/3375-on-ranking-in-survival-analysis-bounds-on-the-concordance-index.pdf
