Intuitive RL (Reinforcement Learning): Introduction to Advantage-Actor-Critic (A2C)

    Hello, Habr! I bring to your attention a translation of the article by Rudy Gilman and Katherine Wang Intuitive RL: Intro to Advantage-Actor-Critic (A2C) .

    Reinforced Learning Specialists (RL) have produced many excellent tutorials. Most, however, describe RL in terms of mathematical equations and abstract diagrams. We like to think about the subject from a different perspective. RL itself is inspired by how animals learn, so why not translate the underlying RL mechanism back into natural phenomena that it is intended to simulate? People learn best through stories.


    This is the story of the Actor Advantage Critic (A2C) model. The subject-critic model is a popular form of the Policy Gradient model, which in itself is a traditional RL algorithm. If you understand A2C, you understand deep RL.


    After you gain an intuitive understanding of A2C, check:

    Illustrations @embermarke


    In RL, the agent, the Klyukovka fox, moves through states surrounded by actions, trying to maximize rewards along the way.

    A2C receives status inputs - sensor inputs in the case of Klukovka - and generates two outputs:
    1) An estimate of how much reward will be received, starting from the moment of the current state, with the exception of the current (existing) reward.
    2) A recommendation on what action to take (policy).

    Critic: wow, what a wonderful valley! It will be a fruitful day for foraging! I bet today I’ll collect 20 points before sunset.
    “Subject”: these flowers look beautiful, I feel a craving for “A”.

    Deep RL models are input-output mapping machines, like any other classification or regression model. Instead of categorizing images or text, deep RL models bring states to actions and / or states to state values. A2C does both.

    This state-action-reward set makes up one observation. She will write this line of data to her journal, but she is not going to think about it yet. She will fill it when she stops to think.

    Some authors associate reward 1 with time step 1, others associate it with step 2, but all have in mind the same concept: the reward is related to the state, and the action immediately precedes it.

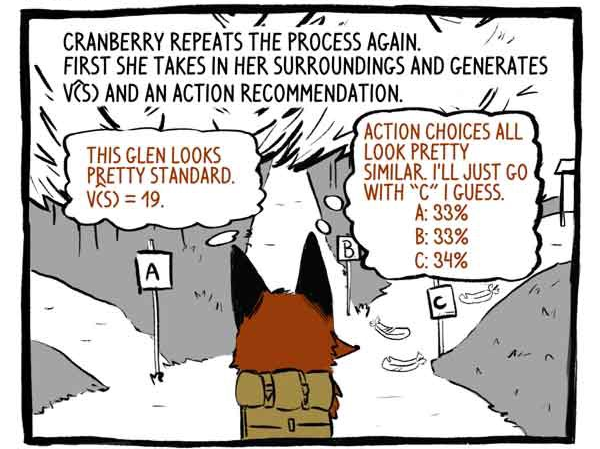
    Hooking repeats the process again. First, she perceives her surroundings and develops a function V (S) and a recommendation for action.

    Critic: This valley looks pretty standard. V (S) = 19.
    “Subject”: The options for action look very similar. I think I'll just go on track “C”.

    Further it acts.

    Receives a reward of +20! And records the observation.

    She repeats the process again.

    After collecting three observations, Klyukovka stops to think.

    Other families of models wait until the very end of the day (Monte Carlo), while others think after each step (one-steps).
    Before she can set up her internal critic, Klukovka needs to calculate how many points she will actually receive in each given state.

    But first!
    Let's look at how Klukovka's cousin, Lis Monte Carlo, calculates the true meaning of each state.

    Monte Carlo models do not reflect their experience until the end of the game, and since the value of the last state is zero, it is very simple to find the true value of this previous state as the sum of the rewards received after this moment.

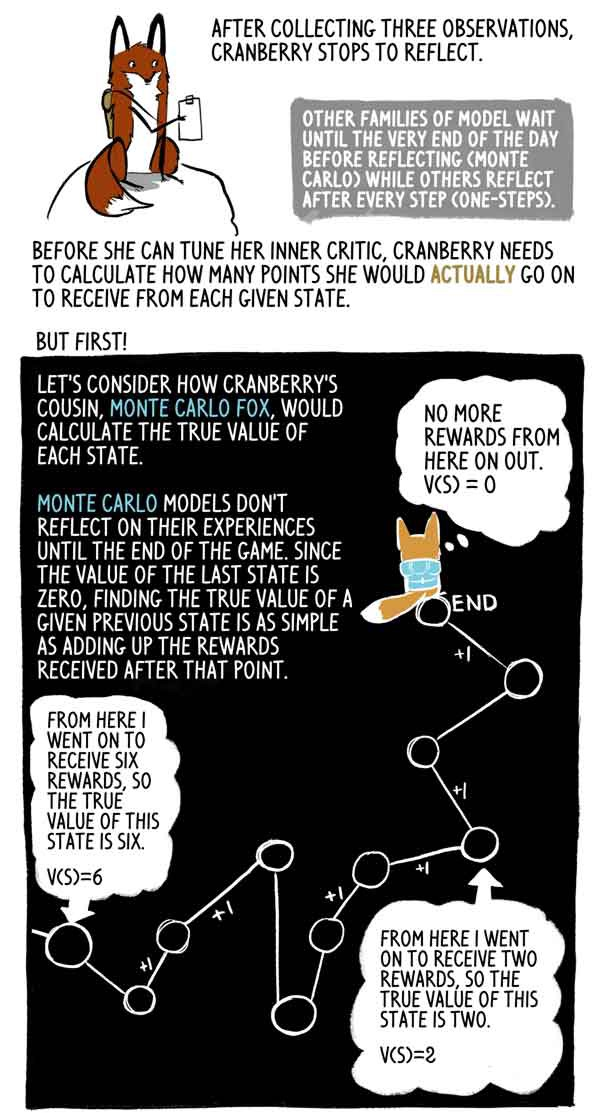
    In fact, this is just a high dispersion sample V (S). The agent could easily follow a different trajectory from the same state, thus receiving a different aggregate reward.


    But Klyukovka goes, stops and reflects many times until the day comes to an end. She wants to know how many points she really will get from each state to the end of the game, because there are several hours left until the end of the game.

    That's where she does something really smart - the Klyukovka fox estimates how many points she will receive for her last fortune in this set. Fortunately, she has the correct assessment of her condition - her critic.
    With this assessment, Klyukovka can calculate the “correct” values ​​of the previous states exactly as the Monte Carlo fox does.

    Lis Monte Carlo evaluates the target marks, making the deployment of the trajectory and adding rewards forward from each state. A2C cuts this trajectory and replaces it with an assessment of its critic. This initial load reduces the variance of the score and allows the A2C to run continuously, albeit by introducing a small bias.

    Rewards are often reduced to reflect the fact that rewards are better now than in the future. For simplicity, Klukovka does not reduce its rewards.

    Now Klukovka can go through each row of data and compare its estimates of state values ​​with its actual values. She uses the difference between these numbers to perfect her prediction skills. Every three steps throughout the day, Klyukovka collects valuable experience that is worth considering.

    “I poorly rated states 1 and 2. What did I do wrong? Yeah! The next time I see feathers like these, I will increase V (S).

    It may seem crazy that Klukovka is able to use her V (S) rating as a basis to compare it with other forecasts. But animals (including us) do this all the time! If you feel that things are going well, you do not need to retrain the actions that brought you into this state.

    By trimming our calculated outputs and replacing them with an initial load estimate, we replaced the large Monte Carlo variance with a small bias. RL models typically suffer from high dispersion (representing all possible paths), and such a replacement is usually worth it.


    Klukovka repeats this process all day, collecting three observations of state-action-reward and reflecting on them.

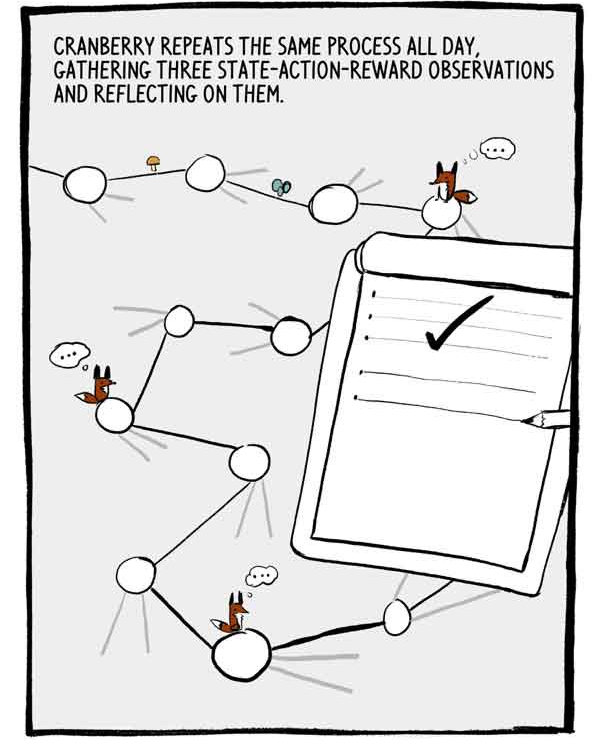
    Each set of three observations is a small, autocorrelated series of labeled training data. To reduce this autocorrelation, many A2Cs train many agents in parallel, adding up their experience together before sending it to a common neural network.

    The day is finally coming to an end. Only two steps left.
    As we said earlier, the recommendations of Klukovka’s actions are expressed in percentage confidence about its capabilities. Instead of just choosing the most reliable choice, Klukovka chooses from this distribution of actions. This ensures that she does not always agree to safe, but potentially mediocre actions.


    I could regret it, but ... Sometimes, exploring unknown things, you can come to exciting new discoveries ...

    To further encourage research, a value called entropy is subtracted from the loss function. Entropy means the “scope” of the distribution of actions.
    - It seems that the game has paid off!

    Or not?

    Sometimes the agent is in a state where all actions lead to negative outcomes. A2C, however, copes well with bad situations.

    When the sun went down, Klyukovka reflected on the last set of solutions.

    We talked about how Klyukovka sets up his inner critic. But how does she fine-tune her inner “subject"? How does she learn to make such exquisite choices?


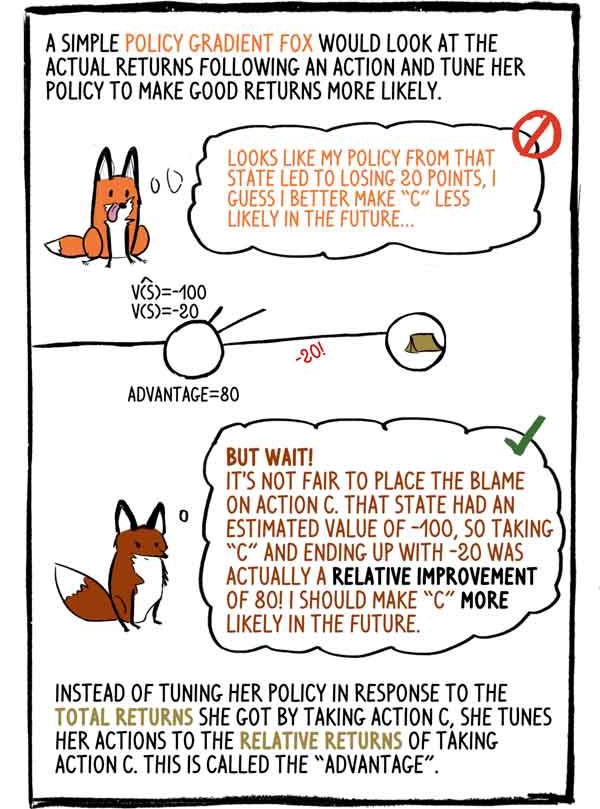
    The simple-minded fox Gradient-Policy would look at the actual income after the action and adjust its policy to make good income more likely: - It seems that my policy in this state led to a loss of 20 points, I think that in the future it is better to do “C” less likely.

    - But wait! It is unfair to blame the action “C”. This condition had an estimated value of -100, so choosing “C” and ending it with -20 was actually a relative improvement of 80! I have to make “C” more likely in the future.

    Instead of adjusting its policy in response to the total revenue it received by selecting action C, it tunes its action to the relative revenues from action C. This is called an “advantage”.

    What we called an advantage is simply a mistake. As an advantage, Klukovka uses it to make actions that were surprisingly good, more likely. As a mistake, she uses the same amount to push her internal critic to improve her assessment of the status value.

    Subject takes advantage:
    “Wow, it worked better than I thought, action C must be a good idea.” The
    critic uses the error:
    “But why was I surprised? I probably shouldn't have evaluated this condition so negatively.”

    Now we can show how the total losses are calculated - we minimize this function to improve our model:
    “Total loss = loss of action + loss of value - entropy”

    Please note that to calculate the gradients of three qualitatively different types, we take the values ​​“through one”. This is effective, but can make convergence more difficult.

    Like all animals, as Klyukovka grows older, he will hone his ability to predict the values ​​of states, gain more confidence in his actions, and less often be surprised at awards.


    RL agents, such as Klukovka, not only generate all the necessary data, simply interacting with the environment, but also evaluate the target labels themselves. That's right, RL models update previous grades to better match new and improved grades.

    As Dr. David Silver, head of the RL group at Google Deepmind says: AI = DL + RL. When an agent like Klyukovka can set his own intelligence, the possibilities are endless ...

    Tags:

    Also popular now: