Forecasting again, part 2
Today I will describe some more time series prediction properties.
Namely, the cyclical nature and complexity of the variant with similarity of segments.

Let's return to the schedule from the previous article . That graph is very periodic (see the picture further), and it would be correct to first predict it by calculating the cycles. From using only the calculation of cyclicality, I got a forecast of a 4.1% error (mape) instead of 5% for the former experimental point.
After calculating the cycles, we do the subtraction from the original values of the graph, the values of the forecast from the cycles, and the resulting graph of the error is already trying to predict the correlations. As a result, for the same point I got already 3.7% error.
The program and its source code for the current version here.. Now it looks more like a standalone series prediction utility than testing a single method and a single graph. And can perform the forecast for the last point for which there is no actual predicted value.
ape - Absolute percentage error - abs (forecast-fact) / fact
mape - Mean absolute percentage error
If we take several ape for the period and calculate the arithmetic average value, we get the mape.
By itself, the percentage of forecast error for an unknown graph says little. Because it is not known how much the graph usually changes, and, accordingly, whether it is much predicted or little. It is convenient to take for comparison the mape from the forecast, which is made from the assumption that the next value will be the same as the last known one.
For the experimental point this value is 9.2%. Let me remind you that there the figures were cited as a forecast for the day ahead. Those. fluctuations of the schedule for the day is 9.2%. As a result of the use of prediction, this error was reduced to 3.7%.
This is how the analyzed graph looks like in a few days, with strong daily fluctuations:
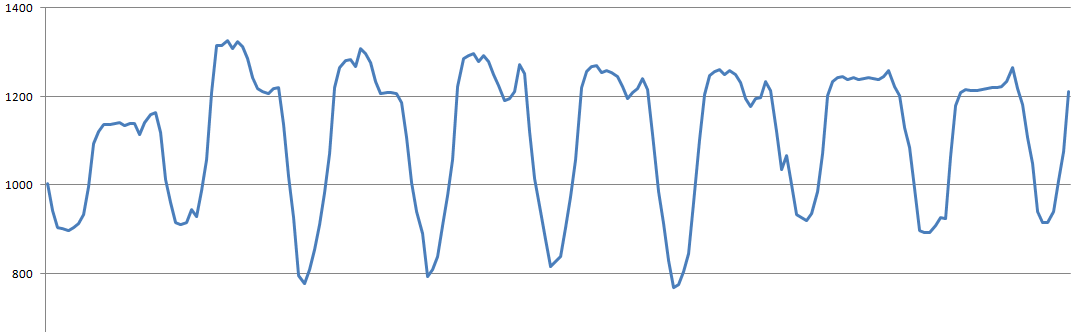
Obviously, if such a schedule is attempted by correlations, then the correlation will see mainly daily fluctuations, while smaller nuances will be drowned.
This is how the forecast for the day ahead looks like this: The
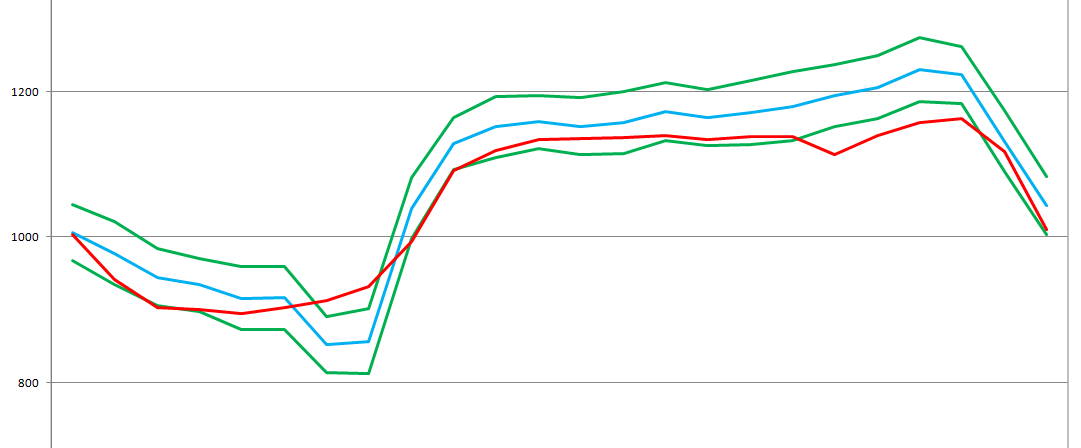
actual graph is displayed in red, the forecast in blue is green, the border of the three standard deviations of the forecast from the center is green if the oscillations of the graph would have a standard distribution then this would be 99% of the likely corridor graph.
In order to make a prediction of cycles, the Cicling class was organized in the files cicling.h and cicling.cpp . An object of this class accumulates N elements of averages, the number of which corresponds to the cycle length. The averages are accumulated by a tunable formula, they are called moving averages.
In my interpretation, this formula has an adjustment length, which is more convenient than if just a faceless coefficient. This mechanism is contained in the compact class MeanAdapt in the file dispersion.h and dispersion.cpp .
On average, the essence of the mechanism is as follows:
In that class there is also a complication with a negative interpretation of cnt_adapt, if you are interested in looking at the sources.
In general, in the Cicling class there are N elements of adaptive means, among them there is the current element, to which the next value is added, and the pointer moves to the next element of the means. When the last element is reached, the pointer moves to the beginning. And so in a circle. More precisely, the class is simply made ar_means [cnt_values% size_cicling] , where cnt_values is the number of added values.
Before adding a new value to the current element of averages, the current average is subtracted from the new value, thereby forming the error value. Class ciclingmay recursively contain the next level of cyclicity Cicling * ne_level , if so, then the error of the current level is passed on to sum up the following cycles, otherwise the error is returned. For the current schedule, the main cycles are daily - 24 hours and weekly - 168 hours.
This forms the difference between the actual value transmitted and the current value of the cyclic averages. If we apply zero to this mechanism in the opposite direction, and add all the averages of the current step to it, but only without modifying the elements of MeanAdapt, then we obtain the value of the forecast from the assumption that the future error is zero. We shift the current element of the medium to the next, all the same without modification, and again in the reverse order we give zero. The result is a forecast graph based on the summation of all averages.
For this mechanism, two questions remain: how to determine the frequency of possible cycles, and how to determine the best adaptation length.
I did it just by searching through test data. The program has a button for scanning cycles, which scans all possible periods of cycles with a dimension of up to two thousand, and gives the best of them.
This best manual is added to the “Periods of cycles” field and the next time the search is started, the cycles will already be scanned minus the new added cycle. Only if you check on the current graph, then the best cyclicities are already entered in the field by default and will no longer be found. Therefore, erase them and run.
The length of the adaptation is also selected by enumeration, but there is no need to indicate anywhere, the program scans it again each time it is started, since that's not for long. The sequence of specifying periods in the Cycle Periods field is also unimportant, since at startup, the best sequence will be selected.
With cycles like everything. They are considered, subtracted from the graph, we get the error graph.
This graph of errors represents fluctuations with an average close to zero — plus and minus errors. It may contain correlations, and may be the remaining random component. To him already and apply the correlation of segments.
And on this issue I will say that it is not the best option to count it according to Pearson's correlation. For this there is a logical reasoning - this correlation rakes up under the semblance of different intensity graphics, although at different intensity the subsequent behavior does not mean at all that it will be the same, only with the transfer. And practical indications - after the application of cycles, an attempt to apply the Pearson correlation only worsens the result. And also when using it without cyclicity, it gets a worse prognosis than cycling does.
As a result of experiments, I came to the conclusion that the best calculation of similarities is just a quadratic difference between the graphs. If the graph is already minus the cycles, then the graph hangs around zero, and the quadratic difference between them is sufficient.
If the cyclicity is not subtracted, then the quadratic difference is better, but with the preliminary subtraction of the mean:

Although I am writing here that this is a correlation of segments, I actually mean a quadratic difference between them.
In the demo program, you can choose different versions of similarities / correlations that I checked, and check them for other graphs you want. Implementation of the calculation of similarities in the program is carried out by the CorrSlide class in the files corr_slide.h and corr_slide.spp. Formulas of various similarities are calculated in the CorrSlide :: Res method . CorrSlide :: get_res (...) .
In addition to the above different calculation options, this class includes optimization, so that you would not have to recalculate the calculation for adjacent segments of the properties described below.
I made that for each position many different correlation lengths are scanned. The first length is taken, say 6 points, the next version of the length is twice as long, i.e. 12, then the next 24, and so on ... For each length, a pack of the best of these segments is accumulated and considers the average forecast and variance. Then, from all counted packs, each of which is responsible for a different length, the one that best predicts the current point is selected. The one that has the smallest variance of the forecast is the best.
It is wrong to assume that the longest segment will be the best. Firstly, for a long segment it may not be enough of quite similar segments, or not at all. And to take one best in likeness, as I mentioned in the previous article, would be wrong. Secondly, the forecast may correlate from substantially closer values to the predicted point, and the subsequent lengthening of the segment will not give a better answer, but will only dilute the pack of the best with unnecessary segments.
But the shortest segment, as you know, the same will not be the best. As a result, several packs of correlating segments of different lengths are simply collected, and it looks like which of the packs has the most specific prediction - the smallest variance.
I also made a variant of calculating the similarity with increasing significance of values closer to the predicted point. There for each increase in length twice, the segment, which was shorter in half, is added twice.
Plus, I also made an exclusion mechanism. In principle, outliers should actually be counted, as elements of a graph or as probable errors. But they should be taken into account at the level of formation of the distributions characteristic of the current schedule. Now I have based my calculations mainly on the principles of working correctly on standard distributions. Therefore, the current version simply indicates how many extreme points to exclude. It is indicated in the “Number of emissions” field, and this is applied in several moments of the calculation, which significantly distorted the result.
The same problem with distributions affects the coefficient of forecasting, about which I wrote in the previous article, it turns out not visual. Analysis of these issues left on the next version of the program.
As a result, all this diversity and disgrace leads to the fact that after subtracting cyclicality, this graph can be predicted a little better.
If you try different versions of the length of such segments, the success of the forecast may vary somewhat. Those. The result is not stable. If at the same time to use the similarity of the square deviation, then it in principle always improves the result after processing cyclicities, in contrast to the Pearson correlation. Also slightly better results are obtained using the similarity lengths of multiples of 24 - the minimum cyclicity.
The calculation is carried out quickly enough that you can specify that a thousand or more positions would be counted and look at the average forecast for this segment, make sure that the forecast is not only at the experimental point. Although not everywhere so striking.
For example, for the period of 1000 positions, with prediction of each step 1 step forward, the result is: the
average error for the selected period is 1.76473% of the average error
only by cycling 1.78332% of the average error
provided that the forecast is the last known position 4.19216%
If the field “Number of forecast positions” should be left empty, then the calculation will be carried out for each position starting from “Date / position of the beginning of the forecast” until the end of the graph.
If it is interesting to see the numbers that I gave regarding the experimental point, then in the default settings, you need to change “Number of prediction positions” = 1, “Number of one position” = 24.
It is worth noting that all these improvements did not allow the forecasting of EURUSD to be shifted to the slightest bit. It seems well, not at all dependent on its past history. Although I will still check it with the next versions of the program.
As mentioned, the program is universal, you can select your data files in it, and specify the predicted column and the date column if there is one. The column separator can be a comma or a semicolon. The program, if possible, provides descriptions of controls.

The program and its source .
For now, next time I will improve the result of forecasting with new properties.
Namely, the cyclical nature and complexity of the variant with similarity of segments.

Let's return to the schedule from the previous article . That graph is very periodic (see the picture further), and it would be correct to first predict it by calculating the cycles. From using only the calculation of cyclicality, I got a forecast of a 4.1% error (mape) instead of 5% for the former experimental point.
After calculating the cycles, we do the subtraction from the original values of the graph, the values of the forecast from the cycles, and the resulting graph of the error is already trying to predict the correlations. As a result, for the same point I got already 3.7% error.
The program and its source code for the current version here.. Now it looks more like a standalone series prediction utility than testing a single method and a single graph. And can perform the forecast for the last point for which there is no actual predicted value.
And now more about the algorithms and meanings
ape - Absolute percentage error - abs (forecast-fact) / fact
mape - Mean absolute percentage error
If we take several ape for the period and calculate the arithmetic average value, we get the mape.
By itself, the percentage of forecast error for an unknown graph says little. Because it is not known how much the graph usually changes, and, accordingly, whether it is much predicted or little. It is convenient to take for comparison the mape from the forecast, which is made from the assumption that the next value will be the same as the last known one.
For the experimental point this value is 9.2%. Let me remind you that there the figures were cited as a forecast for the day ahead. Those. fluctuations of the schedule for the day is 9.2%. As a result of the use of prediction, this error was reduced to 3.7%.
This is how the analyzed graph looks like in a few days, with strong daily fluctuations:

Obviously, if such a schedule is attempted by correlations, then the correlation will see mainly daily fluctuations, while smaller nuances will be drowned.
This is how the forecast for the day ahead looks like this: The

actual graph is displayed in red, the forecast in blue is green, the border of the three standard deviations of the forecast from the center is green if the oscillations of the graph would have a standard distribution then this would be 99% of the likely corridor graph.
Calculation of cycles
In order to make a prediction of cycles, the Cicling class was organized in the files cicling.h and cicling.cpp . An object of this class accumulates N elements of averages, the number of which corresponds to the cycle length. The averages are accumulated by a tunable formula, they are called moving averages.
In my interpretation, this formula has an adjustment length, which is more convenient than if just a faceless coefficient. This mechanism is contained in the compact class MeanAdapt in the file dispersion.h and dispersion.cpp .
On average, the essence of the mechanism is as follows:
cnt_vals = cnt_vals + 1;
if (cnt_vals > cnt_adapt)
su = su - su / (double)cnt_adapt + new_value;
else
su = su + new_value;
mean = su / (double)min(cnt_vals, cnt_adapt);
In that class there is also a complication with a negative interpretation of cnt_adapt, if you are interested in looking at the sources.
In general, in the Cicling class there are N elements of adaptive means, among them there is the current element, to which the next value is added, and the pointer moves to the next element of the means. When the last element is reached, the pointer moves to the beginning. And so in a circle. More precisely, the class is simply made ar_means [cnt_values% size_cicling] , where cnt_values is the number of added values.
Before adding a new value to the current element of averages, the current average is subtracted from the new value, thereby forming the error value. Class ciclingmay recursively contain the next level of cyclicity Cicling * ne_level , if so, then the error of the current level is passed on to sum up the following cycles, otherwise the error is returned. For the current schedule, the main cycles are daily - 24 hours and weekly - 168 hours.
This forms the difference between the actual value transmitted and the current value of the cyclic averages. If we apply zero to this mechanism in the opposite direction, and add all the averages of the current step to it, but only without modifying the elements of MeanAdapt, then we obtain the value of the forecast from the assumption that the future error is zero. We shift the current element of the medium to the next, all the same without modification, and again in the reverse order we give zero. The result is a forecast graph based on the summation of all averages.
For this mechanism, two questions remain: how to determine the frequency of possible cycles, and how to determine the best adaptation length.
I did it just by searching through test data. The program has a button for scanning cycles, which scans all possible periods of cycles with a dimension of up to two thousand, and gives the best of them.
This best manual is added to the “Periods of cycles” field and the next time the search is started, the cycles will already be scanned minus the new added cycle. Only if you check on the current graph, then the best cyclicities are already entered in the field by default and will no longer be found. Therefore, erase them and run.
The length of the adaptation is also selected by enumeration, but there is no need to indicate anywhere, the program scans it again each time it is started, since that's not for long. The sequence of specifying periods in the Cycle Periods field is also unimportant, since at startup, the best sequence will be selected.
With cycles like everything. They are considered, subtracted from the graph, we get the error graph.
My version of the implementation of the similarity of segments
This graph of errors represents fluctuations with an average close to zero — plus and minus errors. It may contain correlations, and may be the remaining random component. To him already and apply the correlation of segments.
And on this issue I will say that it is not the best option to count it according to Pearson's correlation. For this there is a logical reasoning - this correlation rakes up under the semblance of different intensity graphics, although at different intensity the subsequent behavior does not mean at all that it will be the same, only with the transfer. And practical indications - after the application of cycles, an attempt to apply the Pearson correlation only worsens the result. And also when using it without cyclicity, it gets a worse prognosis than cycling does.
As a result of experiments, I came to the conclusion that the best calculation of similarities is just a quadratic difference between the graphs. If the graph is already minus the cycles, then the graph hangs around zero, and the quadratic difference between them is sufficient.
If the cyclicity is not subtracted, then the quadratic difference is better, but with the preliminary subtraction of the mean:

Although I am writing here that this is a correlation of segments, I actually mean a quadratic difference between them.
In the demo program, you can choose different versions of similarities / correlations that I checked, and check them for other graphs you want. Implementation of the calculation of similarities in the program is carried out by the CorrSlide class in the files corr_slide.h and corr_slide.spp. Formulas of various similarities are calculated in the CorrSlide :: Res method . CorrSlide :: get_res (...) .
In addition to the above different calculation options, this class includes optimization, so that you would not have to recalculate the calculation for adjacent segments of the properties described below.
I made that for each position many different correlation lengths are scanned. The first length is taken, say 6 points, the next version of the length is twice as long, i.e. 12, then the next 24, and so on ... For each length, a pack of the best of these segments is accumulated and considers the average forecast and variance. Then, from all counted packs, each of which is responsible for a different length, the one that best predicts the current point is selected. The one that has the smallest variance of the forecast is the best.
It is wrong to assume that the longest segment will be the best. Firstly, for a long segment it may not be enough of quite similar segments, or not at all. And to take one best in likeness, as I mentioned in the previous article, would be wrong. Secondly, the forecast may correlate from substantially closer values to the predicted point, and the subsequent lengthening of the segment will not give a better answer, but will only dilute the pack of the best with unnecessary segments.
But the shortest segment, as you know, the same will not be the best. As a result, several packs of correlating segments of different lengths are simply collected, and it looks like which of the packs has the most specific prediction - the smallest variance.
I also made a variant of calculating the similarity with increasing significance of values closer to the predicted point. There for each increase in length twice, the segment, which was shorter in half, is added twice.
This is what it looks like ...
This is how it looks, the following amounts are the components of the correlation formulas:
void CorrSlide::make_res_2() {
for (int i_len = 0; i_len < c_lens-1; ++i_len) {
Calc& calc = ar_calc_2[i_len];
if (i_len == 0)
calc = ar_calc[i_len];
else
calc = ar_calc_2[i_len-1];
Calc& calc_plus = ar_calc[i_len+1];
calc.cnt += calc_plus.cnt;
calc.su_s += calc_plus.su_s;
calc.su_s_pow2 += calc_plus.su_s_pow2;
calc.su_m += calc_plus.su_m;
calc.su_m_pow2 += calc_plus.su_m_pow2;
calc.su_s_m += calc_plus.su_s_m;
calc.div_s = dbl(calc.cnt) * calc.su_s_pow2 - calc.su_s * calc.su_s;
}
}
And a little about emissions
Plus, I also made an exclusion mechanism. In principle, outliers should actually be counted, as elements of a graph or as probable errors. But they should be taken into account at the level of formation of the distributions characteristic of the current schedule. Now I have based my calculations mainly on the principles of working correctly on standard distributions. Therefore, the current version simply indicates how many extreme points to exclude. It is indicated in the “Number of emissions” field, and this is applied in several moments of the calculation, which significantly distorted the result.
The same problem with distributions affects the coefficient of forecasting, about which I wrote in the previous article, it turns out not visual. Analysis of these issues left on the next version of the program.
What happened in the end
As a result, all this diversity and disgrace leads to the fact that after subtracting cyclicality, this graph can be predicted a little better.
If you try different versions of the length of such segments, the success of the forecast may vary somewhat. Those. The result is not stable. If at the same time to use the similarity of the square deviation, then it in principle always improves the result after processing cyclicities, in contrast to the Pearson correlation. Also slightly better results are obtained using the similarity lengths of multiples of 24 - the minimum cyclicity.
The calculation is carried out quickly enough that you can specify that a thousand or more positions would be counted and look at the average forecast for this segment, make sure that the forecast is not only at the experimental point. Although not everywhere so striking.
For example, for the period of 1000 positions, with prediction of each step 1 step forward, the result is: the
average error for the selected period is 1.76473% of the average error
only by cycling 1.78332% of the average error
provided that the forecast is the last known position 4.19216%
If the field “Number of forecast positions” should be left empty, then the calculation will be carried out for each position starting from “Date / position of the beginning of the forecast” until the end of the graph.
If it is interesting to see the numbers that I gave regarding the experimental point, then in the default settings, you need to change “Number of prediction positions” = 1, “Number of one position” = 24.
It is worth noting that all these improvements did not allow the forecasting of EURUSD to be shifted to the slightest bit. It seems well, not at all dependent on its past history. Although I will still check it with the next versions of the program.
As mentioned, the program is universal, you can select your data files in it, and specify the predicted column and the date column if there is one. The column separator can be a comma or a semicolon. The program, if possible, provides descriptions of controls.

The program and its source .
For now, next time I will improve the result of forecasting with new properties.
