Ticket to Ride.Europe - modest steps in the arithmetic of the game
The first day. We were given the game “Ticket to ride. Europe". This is my first acquaintance with the game in this series, you must definitely try and check out.
Fifth day. Somehow tired of losing regularly, it would be time to call for help math and thus try to win a well-deserved victory.
With the help of Google, excel and pythonand the devil mother , a cognitive excursion into the mechanics of the game was conducted.There was no magic pill, but something useful came out.
Points in the game can be scored in four different ways. The proposed theory is well suited for one of them called “build a large number of routes.”
If you carefully calculate all the color runs between cities, it turns out that the maximum demand for trailers is about the same. However, if you turn on the "correction factor" for areas other than the normal haul, the situation will change significantly (the difference between the most demanded and less needed colors reaches almost 20%).
Having driven all 90 tracks through a program written according to these simple rules, we get the output (the total number of sections of the desired color and the “real” demand for cars are indicated):

Gray cars are absent in nature - they are replaced with the right amount of any color during the construction of a haul. Confusion with integer and fractional delimiters arises from the use of two tools — Excel and Python, each of which represents real numbers in its own way. It would be possible to dig into the display settings, but why? This does not affect the results. The
first advice is born from here: In general, it is more profitable to use black or white cars for the construction of “gray” routes. Green and blue, if possible, should be held and used as intended.
And again, the good old Monte Carlo, who thinks how many times you need to take two cards "blindly" (read: spend moves) to get the right number of cars and / or locomotives to build the leg of the desired length and type. For the construction of the stage, one more move is needed, the output is the following table:

which gives little by itself, but serves as a basis for future calculations.
The double color tunnel “Pamplona-Madrid” (3 cars long) did not enter the table, for it the number of moves was calculated separately, it amounts to 7.511.
In the upper left corner of the map is the city of Edinburgh, one double way from London approaches it. At the same time, Edinburgh is the terminal station for two routes (Edinburgh-Athens (21) and Edinburgh-Paris (7)). That is, when playing with two or three, there is a possibility that a war will unfold over London-Edinburgh and one of the players will remain with an unfinished route.
For 4 more cities, the number of suitable routes coincides with the number of routes starting or ending in this city.
Tip Two: If your routes start or end in specified cities, build paths in the right direction at the earliest opportunity.
If we restrict ourselves not only to the end stations, but also to the intermediate ones (see the fifth “revelation” on the method of “calculating” intermediate stations), we get a kind of rating of “loaded” cities that need to be “girdled” first.
At the other end of the ranking are located cities that are of little interest in terms of routes - they can be left for later, at the very end of the game (the main thing is to have enough cars).
The following data is currently available:
It is quite possible to find the fastest way for each route (the way in which you can build a route in the least number of moves). Dijkstra's algorithm is quite suitable for this , the number of moves required to build it is used as weights for the hauls.
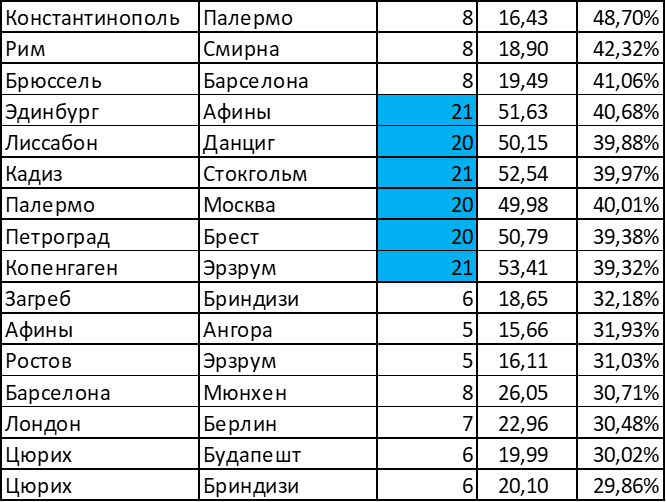
The table below shows the most and least profitable routes, the “benefit” of the routes (the number of points received / the number of moves spent) varies quite noticeably, while the “long routes” (highlighted in blue) go confidently at the top of the table:
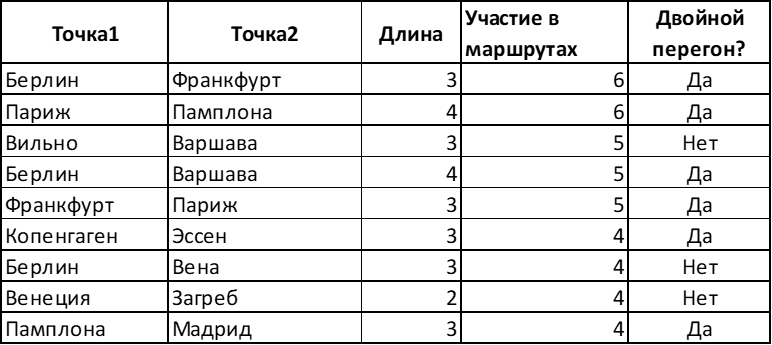
When the list of the most optimal paths is ready, you can estimate the “workload” of each of the hauls and select the “key” sections that are used in the greatest number of routes.
Due to the obvious demand for these areas, sooner or later a struggle will arise for them. And it will be better if the problems with the employment of sites arise early for your rivals.
Tip Three: In the event that your route passes through the hauls indicated above (and through the stage Edinburgh-London), take them first of all, as far as there are cars of the desired color.
In case 4-5 players are playing, the situation will be somewhat simpler for double hauls.
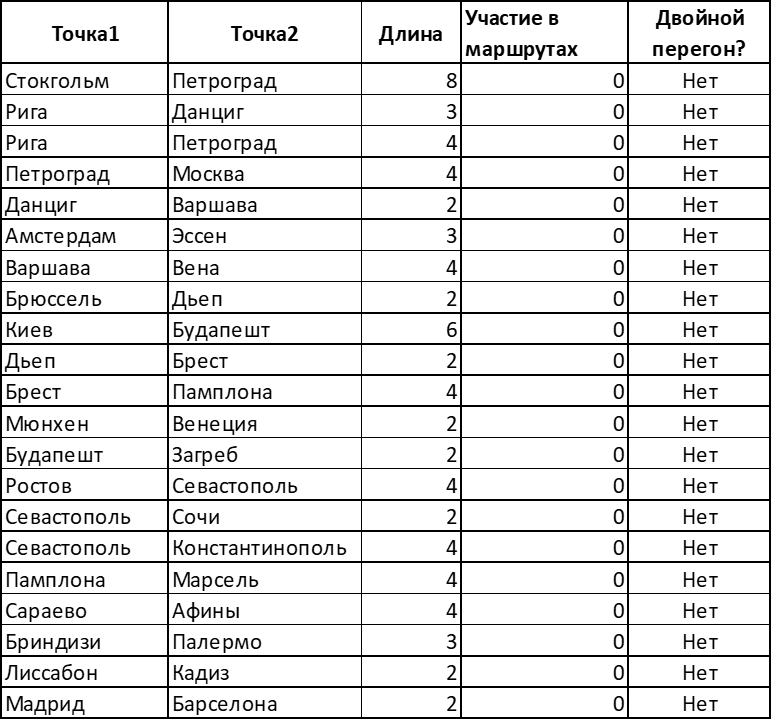
At the other end of the table there are spans that are minimally required in the average game.
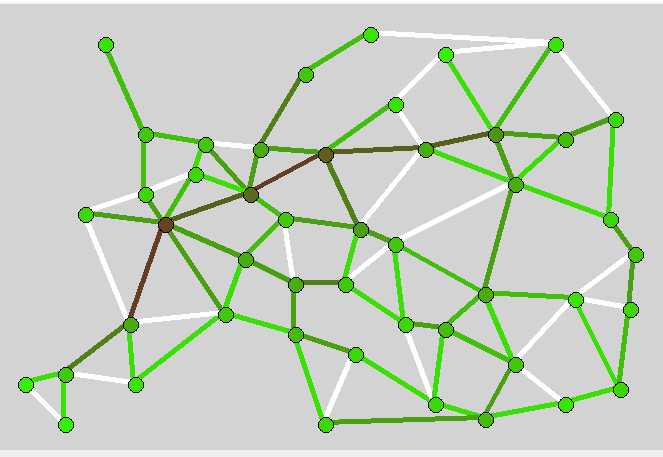
In general, if you look at the heat map of the workload of cities and hauls (the browner the busier; the white color is zero load) from a bird's-eye view, it will become clear where the struggle is most likely to unfold.
These tips can be useful when playing rush-em - the fastest way to build a lot of routes. Mathematization of the most profitable routes between cities (points / number of moves), adding the “longest continuous branch” algorithms, using previously constructed sections and using rivals' paths with the help of stations are still waiting for their researchers.
Wins you and interesting battles.
Continuation of "arithmetic"
Fifth day. Somehow tired of losing regularly, it would be time to call for help math and thus try to win a well-deserved victory.

With the help of Google, excel and python
For those who are not familiar with the game
Если кратко, надо строить маршруты, тратить на них вагончики и зарабатывать очки.
Правила игры — hobbyworld.ru/download/rules/T2RE_rules_new.pdf
Набор в формате «Распечатай и играй» — boardgamer.ru/ticket-to-ride-europe-raspechataj-i-igraj (названия городов на карточках не совпадает с названием городов в текущем посту).
Правила игры — hobbyworld.ru/download/rules/T2RE_rules_new.pdf
Набор в формате «Распечатай и играй» — boardgamer.ru/ticket-to-ride-europe-raspechataj-i-igraj (названия городов на карточках не совпадает с названием городов в текущем посту).
Points in the game can be scored in four different ways. The proposed theory is well suited for one of them called “build a large number of routes.”
Game axioms
- In total, there are 46 cities on the field. Between the cities there are 90 routes, regardless of the type (ferry, tunnel, double). A maximum of 300 wagons are placed on the field (using both hauls in “double” sections) - on average, the haul length is 3.33 wagons
- On the playing field there are the following legs:
Normal distilled Double haul Tunnel Double tunnel Ferry Double ferry Color there is there is there is there is Gray there is there is there is there is
No distillation can be a ferry and a tunnel at the same time.
Revelation one: not all cars are equally useful.
If you carefully calculate all the color runs between cities, it turns out that the maximum demand for trailers is about the same. However, if you turn on the "correction factor" for areas other than the normal haul, the situation will change significantly (the difference between the most demanded and less needed colors reaches almost 20%).
- The need for wagons for a regular haul is estimated as 100% of the haul length (we assume that only the colored wagons are used for the haul).
- The demand for cars for double haul is estimated at 50% (we believe that cars of either of two colors can be used for haul. For example, both white and orange cars can be used for the construction of the Paris-Frankfurt section).
- A liter of coffee was spent in order to calculate the need for wagons for the construction of the tunnel on the basis of the probability theory, and finally it was calculated by the Monte Carlo method. Emulated extraction of three cards from the full deck, fixed the probability of loss of "game cards" - locomotives, or cars of the same color. ( Here and hereafter: every time the probability for the full deck was considered, the cards that may already be in the hands of the users were not taken into account ).
Add. wagons Probability 0 44.14% one 41.95% 2 12.71% 3 1.2%
The total “hospital average” demand for railcars for the construction of a tunnel of length N is: - Double tunnel counts as a mixture of rules 2 and 3
Having driven all 90 tracks through a program written according to these simple rules, we get the output (the total number of sections of the desired color and the “real” demand for cars are indicated):

Gray cars are absent in nature - they are replaced with the right amount of any color during the construction of a haul. Confusion with integer and fractional delimiters arises from the use of two tools — Excel and Python, each of which represents real numbers in its own way. It would be possible to dig into the display settings, but why? This does not affect the results. The
first advice is born from here: In general, it is more profitable to use black or white cars for the construction of “gray” routes. Green and blue, if possible, should be held and used as intended.
Revelation Two: For the construction of hauls of various types, you need a different number of moves.
And again, the good old Monte Carlo, who thinks how many times you need to take two cards "blindly" (read: spend moves) to get the right number of cars and / or locomotives to build the leg of the desired length and type. For the construction of the stage, one more move is needed, the output is the following table:

which gives little by itself, but serves as a basis for future calculations.
The double color tunnel “Pamplona-Madrid” (3 cars long) did not enter the table, for it the number of moves was calculated separately, it amounts to 7.511.
Revelation Three: Not all cities are equally important.
In the upper left corner of the map is the city of Edinburgh, one double way from London approaches it. At the same time, Edinburgh is the terminal station for two routes (Edinburgh-Athens (21) and Edinburgh-Paris (7)). That is, when playing with two or three, there is a possibility that a war will unfold over London-Edinburgh and one of the players will remain with an unfinished route.
For 4 more cities, the number of suitable routes coincides with the number of routes starting or ending in this city.
| City | Ways | The ultimate |
|---|---|---|
| Edinburgh | one | 2 |
| Copenhagen | 2 | 2 |
| Stockholm | 2 | 2 |
| Brest | 3 | 3 |
| Smolensk | 3 | 3 |
Tip Two: If your routes start or end in specified cities, build paths in the right direction at the earliest opportunity.
If we restrict ourselves not only to the end stations, but also to the intermediate ones (see the fifth “revelation” on the method of “calculating” intermediate stations), we get a kind of rating of “loaded” cities that need to be “girdled” first.
| City | Ways | The ultimate | Intermediate |
|---|---|---|---|
| Paris | 7 | 3 | eleven |
| Berlin | five | four | eight |
| Frankfurt | 6 | 2 | 9 |
| Vilna | five | 2 | 6 |
At the other end of the ranking are located cities that are of little interest in terms of routes - they can be left for later, at the very end of the game (the main thing is to have enough cars).
| City | Ways | The ultimate | Intermediate |
|---|---|---|---|
| Sevastopol | five | one | one |
| Petrograd | four | 2 | 0 |
| Riga | 3 | one | 0 |
| Angora | 3 | 2 | 0 |
| Athens | four | 3 | 0 |
| Barcelona | 3 | 2 | 0 |
| Brussels | four | 2 | one |
Revelation the fourth: not all routes are equally useful
The following data is currently available:
- The list of routes from the cards.
- List of hauls between cities.
- The average number of moves you need to spend to build a stage of one type or another.
It is quite possible to find the fastest way for each route (the way in which you can build a route in the least number of moves). Dijkstra's algorithm is quite suitable for this , the number of moves required to build it is used as weights for the hauls.
The table below shows the most and least profitable routes, the “benefit” of the routes (the number of points received / the number of moves spent) varies quite noticeably, while the “long routes” (highlighted in blue) go confidently at the top of the table:

Fifth revelation: not all crossings are equally useful
When the list of the most optimal paths is ready, you can estimate the “workload” of each of the hauls and select the “key” sections that are used in the greatest number of routes.

Due to the obvious demand for these areas, sooner or later a struggle will arise for them. And it will be better if the problems with the employment of sites arise early for your rivals.
Tip Three: In the event that your route passes through the hauls indicated above (and through the stage Edinburgh-London), take them first of all, as far as there are cars of the desired color.
In case 4-5 players are playing, the situation will be somewhat simpler for double hauls.
At the other end of the table there are spans that are minimally required in the average game.

In general, if you look at the heat map of the workload of cities and hauls (the browner the busier; the white color is zero load) from a bird's-eye view, it will become clear where the struggle is most likely to unfold.

These tips can be useful when playing rush-em - the fastest way to build a lot of routes. Mathematization of the most profitable routes between cities (points / number of moves), adding the “longest continuous branch” algorithms, using previously constructed sections and using rivals' paths with the help of stations are still waiting for their researchers.
Wins you and interesting battles.
Continuation of "arithmetic"
