We are doing a machine learning project in Python. Part 1
- Transfer
- Tutorial

Translation of A Complete Machine Learning Project Walk-Through in Python: Part One .
When you read a book or listen to a training course on data analysis, you often get the feeling that you are facing some separate parts of a picture that cannot be put together. You may be scared by the prospect of taking the next step and completely solving a problem with the help of machine learning, but with the help of this series of articles you will gain confidence in the ability to solve any problem in the field of data science.
In order for you to finally have a complete picture in your head, we suggest analyzing from start to finish the project of using machine learning using real data.
Successively go through the steps:
- Cleaning and formatting data.
- Exploratory data analysis.
- Design and selection of features.
- Comparison of the metrics of several machine learning models.
- Hyperparametric tuning of the best model.
- Evaluation of the best model on a test data set.
- Interpretation of the results of the model.
- Conclusions and work with documents.
You will learn how the steps go into one another and how to implement them in Python. The whole project is available on GitHub, the first part lies here. In this article we will consider the first three stages.
Task description
Before writing code, you need to understand the problem being solved and the data available. In this project, we will work with publicly available energy efficiency data for buildings in New York.
Our goal: to use the available data to build a model that predicts the number of Energy Star Score for a particular building, and interpret the results to find factors that influence the final score.
The data already includes the assigned Energy Star Score, so our task is machine learning with controlled regression:
- Supervised: We know the signs and purpose, and our task is to train a model that can match the first to the second.
- Regression: The Energy Star Score is a continuous variable.
Our model must be accurate - so that it can predict the value of the Energy Star Score close to true - and interpretable - so that we can understand its predictions. Knowing the target data, we can use them when making decisions as we go deeper into the data and create the model.
Data cleansing
Not every data set is an ideally matched set of observations, without anomalies and missing values (a hint of the mtcars and iris datasets ). In real data there is little order, so before proceeding with the analysis, they need to be cleaned and brought to an acceptable format. Data cleaning is an unpleasant but obligatory procedure in solving most data analysis tasks.
First you can load the data as a Pandas dataframe and examine them:
import pandas as pd
import numpy as np
# Read in data into a dataframe
data = pd.read_csv('data/Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016_.csv')
# Display top of dataframe
data.head()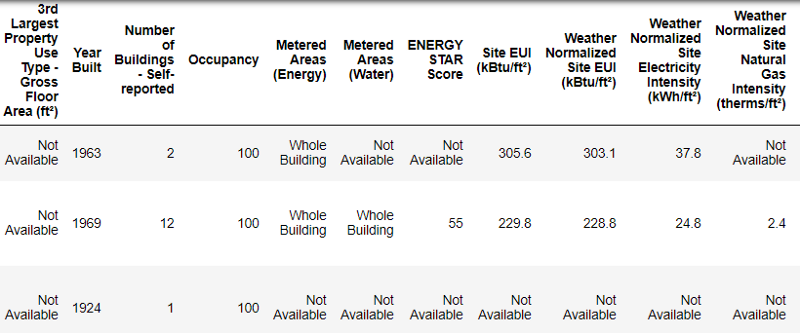
This is how real data looks.
This is a fragment of a table of 60 columns. Even here, several problems are visible: we need to predict
Energy Star Score, but we do not know what all these columns mean. Although this is not necessarily a problem, because you can often create an accurate model without knowing anything about variables. But interpretability is important to us, so we need to find out the meaning of at least a few columns. When we received this data, we did not ask about the values, but looked at the name of the file:
and decided to search for “Local Law 84”. We found this page.which stated that it was a New York law, according to which the owners of all buildings of a certain size should report on energy consumption. A further search helped find all the column values . So do not neglect file names, they can be a good starting point. In addition, this is a reminder so that you do not rush and do not miss something important!
We will not study all the columns, but we will definitely deal with the Energy Star Score, which is described as follows:
Percentile ranking from 1 to 100, which is calculated on the basis of annual reports on energy consumption by owners of buildings independently. Energy Star Score is a relative measure used to compare the energy performance of buildings.
The first problem was solved, but the second remained - missing values, marked as “Not Available”. This is a string value in Python, which means that even strings with numbers will be stored as data types
object, because if there is any string in the column, Pandas converts it to a column that consists entirely of string. Column data types can be found using the method dataframe.info():# See the column data types and non-missing values
data.info()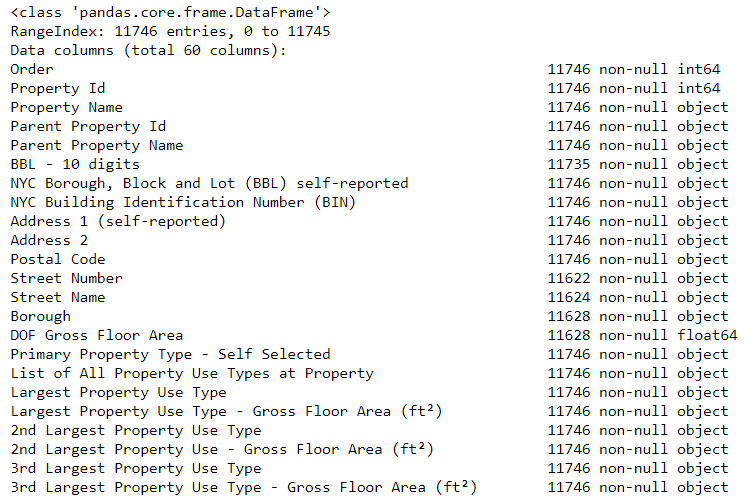
Surely some columns that explicitly contain numbers (such as ft²) are stored as objects. We cannot apply numerical analysis to string values, so we convert them to numerical data types (especially
float)! This code first replaces all “Not Available” with not a number (
np.nan), which can be interpreted as numbers, and then converts the contents of certain columns to type float:# Replace all occurrences of Not Available with numpy not a number
data = data.replace({'Not Available': np.nan})
# Iterate through the columns
for col in list(data.columns):
# Select columns that should be numeric
if ('ft²' in col or 'kBtu' in col or 'Metric Tons CO2e' in col or 'kWh' in
col or 'therms' in col or 'gal' in col or 'Score' in col):
# Convert the data type to float
data[col] = data[col].astype(float)When the values in the corresponding columns with us become numbers, we can begin to examine the data.
Missing and abnormal data
Along with incorrect data types, one of the most common problems is missing values. They may be absent for various reasons, and before training the model, these values must either be filled out or deleted. First, let's find out how many values we have in each column ( code is here ).
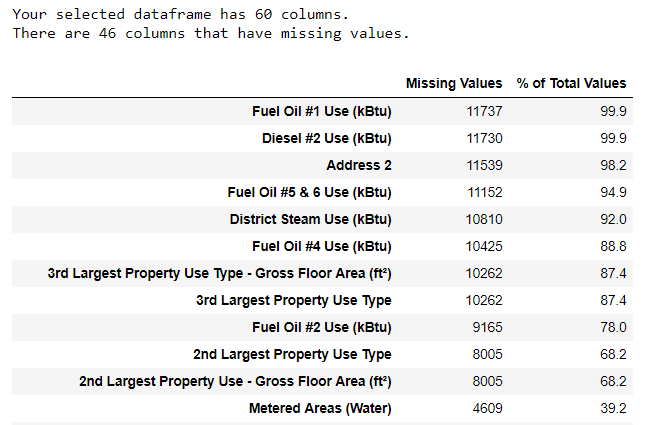
To create a table, a function from a branch on StackOverflow was used .
Information should always be removed with caution, and if there are many values in the column, then it probably will not benefit our model. The threshold after which it is better to throw out the columns depends on your task ( here is a discussion ), and in our project we will delete columns that are more than half empty.
Also at this stage it is better to remove the abnormal values. They can occur due to typos when entering data or due to errors in the units of measurement, or they can be correct but extreme values. In this case, we will remove the "extra" values, guided by the definition of extreme anomalies :
- Below the first quartile is a 3 ∗ interquartile range.
- Above the third quartile + 3 ∗ interquartile range.
The code that removes columns and anomalies is listed on Notepad on Github. Upon completion of the data cleansing process and removal of anomalies, we have more than 11,000 buildings and 49 signs.
Exploratory data analysis
The boring, but necessary stage of data cleaning is finished, you can go to the study! Exploration Data Analysis (RAD) is an unlimited time process in which we calculate statistics and look for trends, anomalies, patterns or relationships in the data.
In short, RAD is an attempt to figure out what data can tell us. Typically, analysis begins with a surface review, then we find interesting fragments and analyze them in more detail. The findings may be interesting in their own right, or they may contribute to the choice of model, helping to decide which features we will use.
Single-variable graphs
Our goal is to predict the value of the Energy Star Score (renamed to our data
score), so it makes sense to start by examining the distribution of this variable. A histogram is a simple but effective way to visualize the distribution of a single variable, and it can be easily built using matplotlib.import matplotlib.pyplot as plt
# Histogram of the Energy Star Score
plt.style.use('fivethirtyeight')
plt.hist(data['score'].dropna(), bins = 100, edgecolor = 'k');
plt.xlabel('Score'); plt.ylabel('Number of Buildings');
plt.title('Energy Star Score Distribution');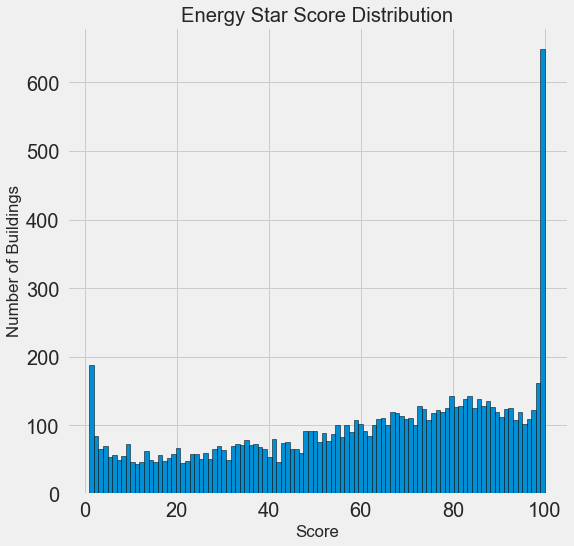
Looks suspicious! The Energy Star Score is a percentile, so you should expect a uniform distribution when each point is assigned to the same number of buildings. However, a disproportionately large number of buildings received the highest and lowest results (for the Energy Star Score, the larger the better).
If we again look at the definition of this score, we will see that it is calculated on the basis of “reports independently filled out by the building owners,” which may explain the excess of very large values. Asking building owners to report their energy consumption is like asking students to report their grades in exams. So this is perhaps not the most objective criterion for assessing the energy efficiency of real estate.
If we had an unlimited supply of time, we could find out why so many buildings got very high and very low points. To do this, we would have to choose the appropriate buildings and carefully analyze them. But we only need to learn how to predict scores, and not develop a more accurate assessment method. You can mark yourself that the points have a suspicious distribution, but we will focus on forecasting.
Relationship search
The main part of the AHFR is the search for the relationship between signs and our goal. Variables correlating with it are useful for use in the model, because they can be used for forecasting. One way to study the effect of a categorical variable (which takes only a limited set of values) on the goal is to plot the density using the Seaborn library.
The density graph can be considered a smoothed histogram because it shows the distribution of a single variable. You can colorize individual classes on a graph to see how a categorical variable changes distribution. This code plots the Energy Star Score density chart, colored according to the type of building (for a list of buildings with more than 100 dimensions):
# Create a list of buildings with more than 100 measurements
types = data.dropna(subset=['score'])
types = types['Largest Property Use Type'].value_counts()
types = list(types[types.values > 100].index)
# Plot of distribution of scores for building categories
figsize(12, 10)
# Plot each building
for b_type in types:
# Select the building type
subset = data[data['Largest Property Use Type'] == b_type]
# Density plot of Energy Star Scores
sns.kdeplot(subset['score'].dropna(),
label = b_type, shade = False, alpha = 0.8);
# label the plot
plt.xlabel('Energy Star Score', size = 20); plt.ylabel('Density', size = 20);
plt.title('Density Plot of Energy Star Scores by Building Type', size = 28);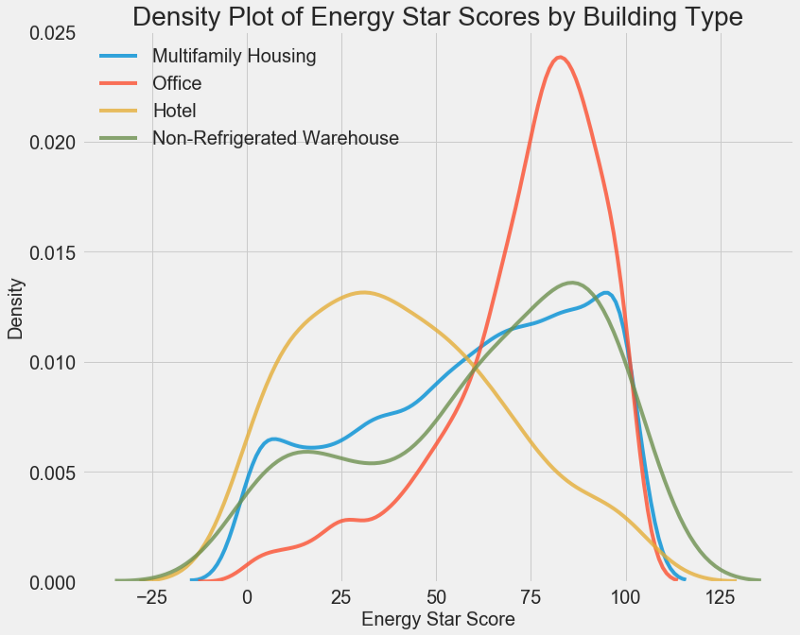
As you can see, the type of building greatly affects the number of points. Office buildings usually have a higher score and hotels lower. So you need to include the type of building in the model, because this sign affects our goal. As a categorical variable, we must perform one-hot coding of the building type.
A similar graph can be used to estimate the Energy Star Score by city
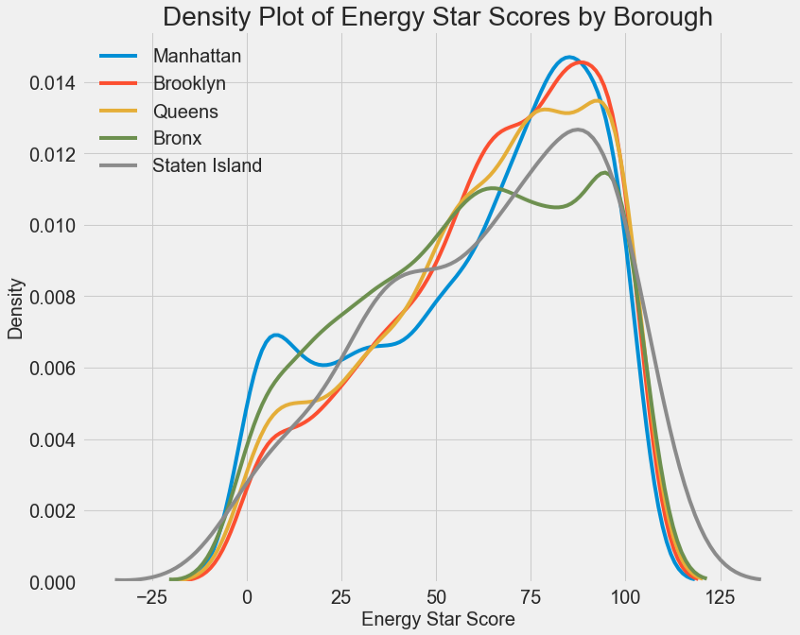
district : The district does not affect the score as much as the type of building. Nevertheless, we will include it in the model, because there is a slight difference between the regions.
To calculate the relationship between the variables, you can use the Pearson correlation coefficient. This is a measure of the intensity and direction of a linear relationship between two variables. A value of +1 means a perfectly linear positive relationship, and -1 means a perfectly linear negative relationship. Here are a few examples of the values of the Pearson correlation coefficient :

Although this coefficient cannot reflect nonlinear dependencies, it is possible to begin with it to evaluate the relationships of variables. In Pandas, you can easily calculate the correlations between any columns in a dataframe:
# Find all correlations with the score and sort
correlations_data = data.corr()['score'].sort_values()The most negative correlations with the goal:

and the most positive:

There are several strong negative correlations between the attributes and the goal, and the largest of them belong to different EUI categories (the methods for calculating these indicators differ slightly). EUI (Energy Use Intensity ) is the amount of energy consumed by a building divided by a square foot of area. This specific value is used to evaluate energy efficiency, and the smaller it is, the better. Logic suggests that these correlations are justified: if the EUI increases, then the Energy Star Score should decline.
Two-variable graphs
We use scatter plots to visualize the relationships between two continuous variables. You can add additional information to the colors of the dots, for example, a categorical variable. The relationship between the Energy Star Score and the EUI is shown below, the different types of buildings are marked with color:
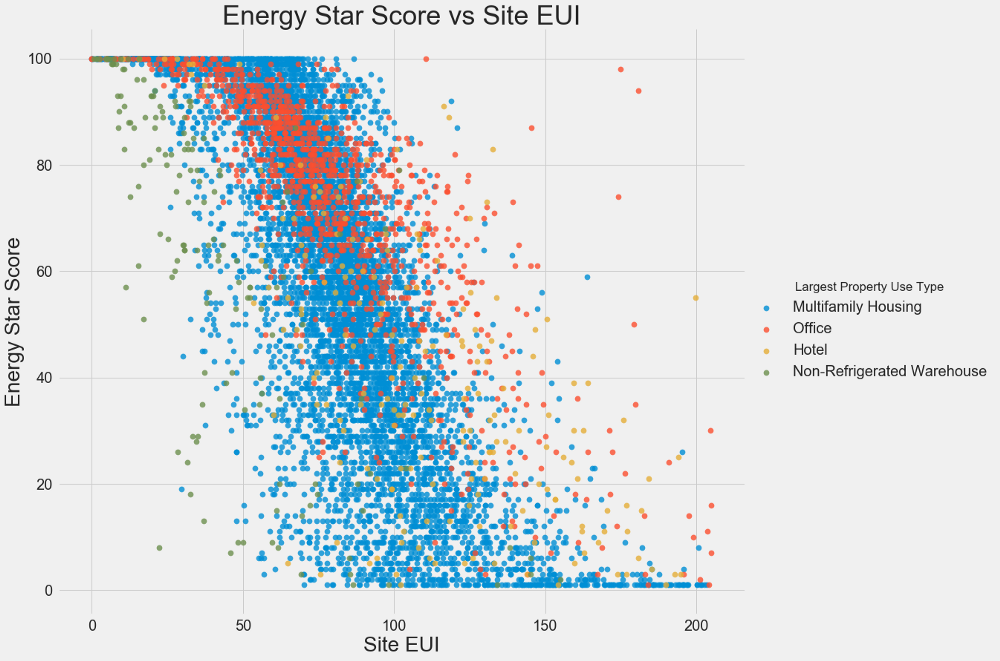
This graph allows you to visualize a correlation coefficient of -0.7. As the EUI decreases, the Energy Star Score increases, this relationship is observed in different types of buildings.
Our latest research chart is called the Pairs Plot . This is a great tool to see the relationships between different pairs of variables and the distribution of single variables. We will use the Seaborn library and function
PairGrid to create a paired graph with a scatter chart in the upper triangle, with a diagonal histogram, a two-dimensional diagram of the core density and correlation coefficients in the lower triangle.# Extract the columns to plot
plot_data = features[['score', 'Site EUI (kBtu/ft²)',
'Weather Normalized Source EUI (kBtu/ft²)',
'log_Total GHG Emissions (Metric Tons CO2e)']]
# Replace the inf with nan
plot_data = plot_data.replace({np.inf: np.nan, -np.inf: np.nan})
# Rename columns
plot_data = plot_data.rename(columns = {'Site EUI (kBtu/ft²)': 'Site EUI',
'Weather Normalized Source EUI (kBtu/ft²)': 'Weather Norm EUI',
'log_Total GHG Emissions (Metric Tons CO2e)': 'log GHG Emissions'})
# Drop na values
plot_data = plot_data.dropna()
# Function to calculate correlation coefficient between two columns
def corr_func(x, y, **kwargs):
r = np.corrcoef(x, y)[0][1]
ax = plt.gca()
ax.annotate("r = {:.2f}".format(r),
xy=(.2, .8), xycoords=ax.transAxes,
size = 20)
# Create the pairgrid object
grid = sns.PairGrid(data = plot_data, size = 3)
# Upper is a scatter plot
grid.map_upper(plt.scatter, color = 'red', alpha = 0.6)
# Diagonal is a histogram
grid.map_diag(plt.hist, color = 'red', edgecolor = 'black')
# Bottom is correlation and density plot
grid.map_lower(corr_func);
grid.map_lower(sns.kdeplot, cmap = plt.cm.Reds)
# Title for entire plot
plt.suptitle('Pairs Plot of Energy Data', size = 36, y = 1.02);
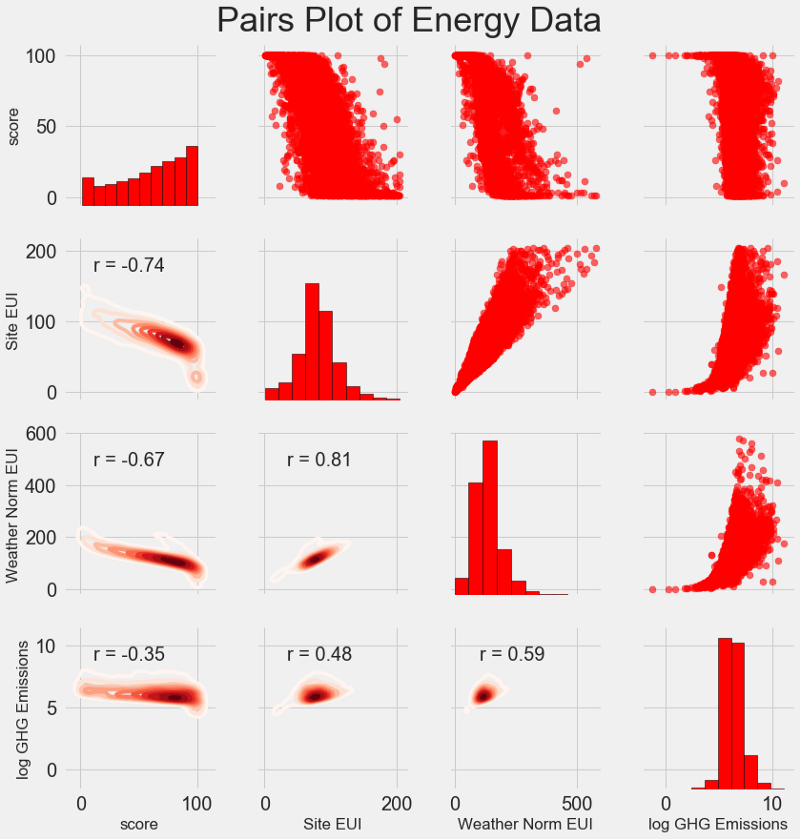
To see the relationship of variables, look for the intersection of rows and columns. Suppose you need to look at the correlation,
Weather Norm EUIand scorethen we look for a row Weather Norm EUIand a column score, at the intersection of which there is a correlation coefficient of -0.67. These graphs not only look cool, but also help you choose variables for the model.Design and selection of features
Designing and selecting features often brings the greatest return in terms of the time spent on machine learning. First we give the definitions:
- Characteristic construction: The process of extracting or creating new characteristics from raw data. To use variables in the model, you may need to transform them, say, take the natural logarithm, or extract the square root, or apply one-hot coding of categorical variables. Characteristic design can be considered as creating additional features from raw data.
- Feature Selection: The process of selecting the most relevant features from data, during which we remove some features to help the model better generalize new data in order to obtain a more interpretable model. The choice of signs can be considered as the removal of “superfluous” so that only the most important remains.
The machine learning model can only learn from the data we provide, so it is extremely important to make sure that we include all the information relevant to our task. If you do not provide the model with the correct data, it will not be able to learn and will not produce accurate forecasts!
We will do the following:
- Applicable to categorical variables (quarter and type of ownership) one-hot coding.
- Add the natural logarithm of all the numerical variables.
One-hot coding is necessary in order to include categorical variables in the model. The machine learning algorithm will not be able to understand the type of “office”, so if the building is an office, we will assign attribute 1 to it, and if not office, then 0.
Adding the converted attributes will help the model learn about non-linear relationships within the data. In the analysis of data, it is normal practice to extract square roots, take natural logarithms or somehow transform the signs , it depends on the specific task or your knowledge of the best techniques. In this case, we will add the natural logarithm of all numerical signs.
This code selects numerical signs, calculates their logarithms, selects two categorical signs, applies one-hot coding to them, and combines both sets into one. Judging by the description, a lot of work remains to be done, but in Pandas everything is pretty simple!
# Copy the original data
features = data.copy()
# Select the numeric columns
numeric_subset = data.select_dtypes('number')
# Create columns with log of numeric columns
for col in numeric_subset.columns:
# Skip the Energy Star Score column
if col == 'score':
next
else:
numeric_subset['log_' + col] = np.log(numeric_subset[col])
# Select the categorical columns
categorical_subset = data[['Borough', 'Largest Property Use Type']]
# One hot encode
categorical_subset = pd.get_dummies(categorical_subset)
# Join the two dataframes using concat
# Make sure to use axis = 1 to perform a column bind
features = pd.concat([numeric_subset, categorical_subset], axis = 1)Now we have more than 11,000 observations (buildings) with 110 columns (tags). Not all signs will be useful for predicting the Energy Star Score, so we will take up the selection of signs and delete some of the variables.
Feature Selection
Many of the 110 signs available are redundant because they strongly correlate with each other. For example, here is a graph of the EUI and Weather Normalized Site EUI, with a correlation coefficient of 0.997.
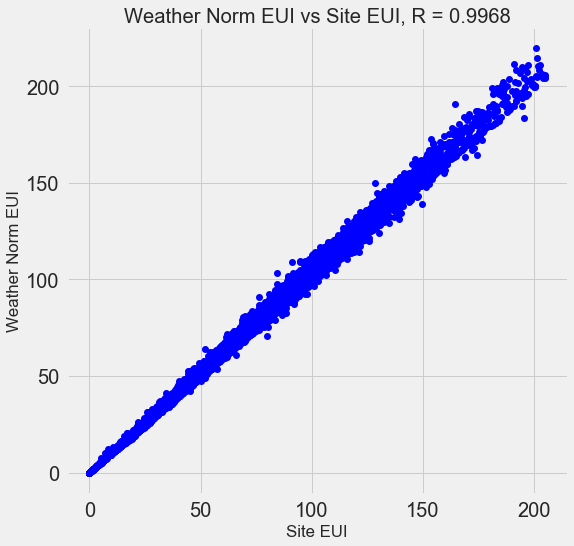
Signs that strongly correlate with each other are called collinear . Removing one variable in such pairs of attributes often helps the model to generalize and be more interpretable . Please note that we are talking about the correlation of some signs with others, and not about correlation with the goal, which would only help our model!
There are a number of methods for calculating the collinearity of features, and one of the most popular is the variance inflation factor.) We will use the bcorrelation coefficient to search and remove collinear features. We discard one pair of signs if the correlation coefficient between them is more than 0.6. The code is in notepad (and in response to Stack Overflow ).
This value looks arbitrary, but in fact I tried different thresholds, and the above allowed me to create the best model. Machine learning is empirical , and often have to experiment to find the best solution. After the selection, we have 64 attributes and one goal left.
# Remove any columns with all na values
features = features.dropna(axis=1, how = 'all')
print(features.shape)
(11319, 65)Choose a base level
We cleared the data, conducted an exploratory analysis, and constructed the signs. And before moving on to creating the model, you need to choose the initial base level (naive baseline) - a kind of assumption with which we will compare the results of the models. If they fall below the basic level, we will assume that machine learning is not applicable for this task, or that a different approach should be tried.
For regression tasks, as a base level, it is reasonable to guess the median value of the goal on the training set for all examples in the test set. These kits set a barrier that is relatively low for any model.
As a metric, we take the average absolute error (mae) in the forecasts. There are many other metrics for regressions, but I like the tip.choose one metric and use it to evaluate models. And the average absolute error is easy to calculate and interpret.
Before calculating the base level, you need to break the data into training and test sets:
- A training set of attributes is that we provide our model along with the answers during the training. The model must learn to match the characteristics of the goal.
- A test feature set is used to evaluate the trained model. When she processes the test suite, she does not see the correct answers and must predict based on available features only. We know the answers for the test data and can compare the forecasting results with them.
For training, we use 70% of the data, and for testing - 30%:
# Split into 70% training and 30% testing set
X, X_test, y, y_test = train_test_split(features, targets,
test_size = 0.3,
random_state = 42)Now we calculate the indicator for the initial base level:
# Function to calculate mean absolute error
def mae(y_true, y_pred):
return np.mean(abs(y_true - y_pred))
baseline_guess = np.median(y)
print('The baseline guess is a score of %0.2f' % baseline_guess)
print("Baseline Performance on the test set: MAE = %0.4f" % mae(y_test, baseline_guess))The baseline guess is a score of 66.00
Baseline Performance on the test set: MAE = 24.5164
The average absolute error on the test set was about 25 points. Since we evaluate in the range from 1 to 100, the error is 25% - a rather low barrier for the model!
Conclusion
You in this article, we went through the first three stages of solving a problem using machine learning. After setting the task, we:
- Cleaned and formatted raw data.
- Conducted exploratory analysis to study the available data.
- We developed a set of features that we will use for our models.
Finally, we calculated the base level with which we will evaluate our algorithms.
In the next article, we will learn how to use Scikit-Learn to evaluate machine learning models, choose the best model and perform its hyperparametric tuning.
