Scientists have invented new ways to cut pizza

Mathematicians from the University of Liverpool in their new work published several previously unknown ways to partition the disk into equal parts. This work belongs to the section of geometry, studying the so-called parquet floors - tiling of the plane with polygons without gaps and overlaps. Scientists were inspired to find ways to cut pizza, a procedure familiar to most of us.

When tilting the plane with geometric figures (tiles), you can set and solve different problems. One of the most interesting tasks is the use of monohedral tiles. In this case, all the tiles have the same shape, or, more precisely, are congruent. This means that any two tiles can be combined with the help of movements, turns or mirror reflection.

The set of tile shapes used to replace the plane is called proto-tiles. Interestingly, there is no mathematical method that allows you to tell in advance whether it is possible to replace a plane with the help of given protoplates. For example, it is known that out of the following 24 heptamonds (figures composed of seven equilateral triangles), only one is unsuitable for monohedral tiling of a plane. But which one?



In this case - V-shaped. But proof of this is a rather nontrivial task.

However, Liverpool mathematicians, instead of a whole plane, limited themselves to a disk and began to search for monohedral proto-tiles suitable for disk division. One version of such protoplates is known to all. With the standard method of cutting pizza, it is divided into equal segments of a triangular shape, the vertices of which converge in the center of the disk. Scientists decided to answer the question - are there such divisions of the disk into equal figures in which not all of these figures touch the center of the disk?

That is, is it possible to cut pizza into equal parts so as to please both those who like more toppings and those who like more crusts? It turned out that it is possible. Moreover, one version of such cutting has been known for a long time, and is located on the logo of the community of the University of Pennsylvania , which organizes mathematical seminars for students:



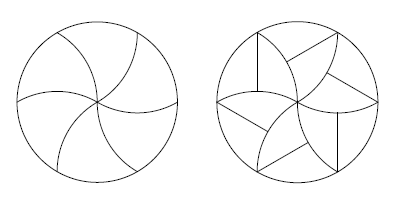
Figured slices can be divided in half, and all parts will be congruent, with only half of them touching the center.

Mathematicians developed this idea and proposed their own methods of dividing a disk into an almost infinite number of equal parts.







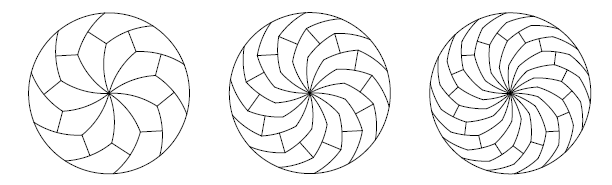
As is often the case in mathematics, the possibilities of applying the ideas of work in practice are not entirely obvious - unless, using a non-standard pizza cutting pizza as a competitive advantage. But on the other hand, to predict how a mathematical discovery will come in handy in the future is also impossible.