Dartess May 13, 2018 at 13:05

BigInt - long arithmetic in JavaScript

Transfer

BigInt- A new numerical primitive data type in JavaScript that allows you to work with numbers of arbitrary precision. With BigIntyou can safely store and process large integers, even beyond the maximum safe integer value Number. In this article we look at some examples of the use BigIntand the new Chrome 67 features, comparing BigIntand Numberin JavaScript.

Examples of using

Arbitrary precision integers open up many new uses for JavaScript.

BigInt helps prevent overflow errors in mathematical operations. This fact in itself makes countless possibilities available, for example, mathematical operations on large numbers are commonly used in financial technology.

Large numeric identifiers and high-precision timestamps cannot be safely represented by a data type Numberin JavaScript. This often leads to errors and forces developers to store them as strings. With BigIntthis data can be represented as numerical values.

BigIntcan be used in a possible data type implementation BigDecimal. This will allow you to store monetary values in the form of decimal fractions without loss of accuracy during operations (for example, without a problem 0.10 + 0.20 !== 0.30).

Earlier in JavaScript, in any of these cases, it was necessary to use libraries that emulate functionality BigInt. When it BigIntbecomes widely available, it will be possible to abandon these dependencies in favor of a natively supported one BigInt. This will help reduce load, parsing and compilation times, as well as increase runtime performance.

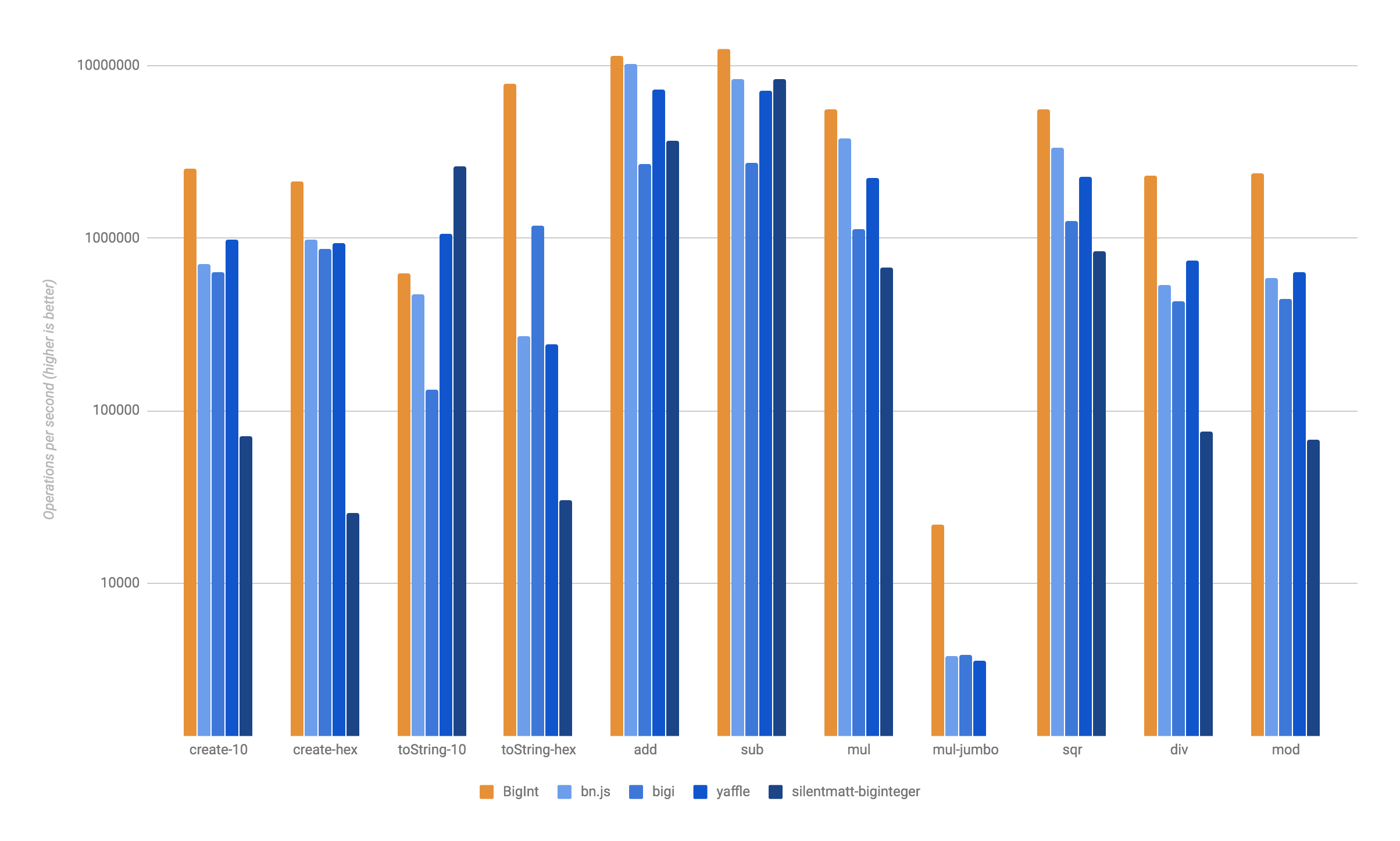
Native BigIntis faster than popular user libraries

A polyphile BigIntrequires a library that implements the necessary functions, as well as a transpilation step, to translate the new syntax into a library API call. Babel currently supports parsing literals BigInt, but does not know how to convert them. Therefore, we do not hope that it BigIntwill be used in production on sites requiring compatibility with a wide range of browsers. However, now that this functionality is starting to appear in browsers, you can start experimenting with BigInt, expecting more and more support for BigInt over time.

Status Quo: Number

The primitive data type Numberin JavaScript is represented by double precision floating-point numbers. The constant Number.MAX_SAFE_INTEGERcontains the maximum possible integer that can be safely increased by one. Its value is equal 2 ** 53-1.

const max = Number.MAX_SAFE_INTEGER;
// → 9_007_199_254_740_991

Note: for readability, I group numbers using underscores as separators. The corresponding sentence would allow the use of such a notation for ordinary JavaScript numeric literals.

Its increase by one gives the expected result:

max + 1;
// → 9_007_199_254_740_992

But if we increase it by another one, Numberwe will not be able to accurately save the result:

max + 2;
// → 9_007_199_254_740_992

Note that the result of the expression max + 1will be equal to the result of the expression max + 2. Therefore, whenever we get this particular value in JavaScript, we cannot say whether it is accurate or not. Any calculations with integers outside the safe integer range (i.e., from Number.MIN_SAFE_INTEGERto Number.MAX_SAFE_INTEGER) are potentially inaccurate. For this reason, we can only rely on integer values in a safe range.

New: BigInt

To create, BigIntjust add a suffix nto the literal notation of an integer. For example, it 123will 123n. The global function BigInt(number)can be used to cast the number to BigInt. In other words, BigInt(123) === 123n. Let's use this to solve the problems that we talked about above:

BigInt(Number.MAX_SAFE_INTEGER) + 2n;
// → 9_007_199_254_740_993n

Here is another example, with the multiplication of two numbers like Number:

1234567890123456789 * 123;
// → 151851850485185200000

If we look at the low-order digits, 9and 3, it can be argued that the result of the multiplication should end with 7(because 9 * 3 === 27). But the result ends with a set of zeros. Something went wrong. Let's try again with BigInt:

1234567890123456789n * 123n;
// → 151851850485185185047n

This time the result is correct.

The limits for working safely with integers are not applicable BigInt, so BigIntwe can use long arithmetic without worrying about loss of precision.

New primitive data type

BigIntIs a new primitive data type in the JavaScript language, so it gets its own type, which the operator can return typeof:

typeof 123;
// → 'number'
typeof 123n;
// → 'bigint'

Since it BigIntis an independent data type, a type number BigIntcan never be strictly equal to a type number Number(for example, 42n !== 42). To compare the type number BigIntand the type number Number, convert one of them to the type of the other before doing the comparison, or use comparison with type conversion ( ==):

42n === BigInt(42);
// → true
42n == 42;
// → true

When cast to a boolean value (for example, in if, when using &&either ||, or as a result of an expression Boolean(int), and so on), type numbers BigIntbehave exactly like type numbers Number.

if (0n) {
  console.log('if');
} else {
  console.log('else');
}
// → logs 'else', because `0n` is falsy.

Operators

BigIntsupports most operators. Binary +, -, *and **operate as usual. /and %also work by rounding the result to the nearest whole if necessary. Bitwise operators |, &, <<, >>and ^work with numbers of type BigIntsimilar to the type numbers Numberwhen negative numbers are represented in binary form as an extra code.

(7 + 6 - 5) * 4 ** 3 / 2 % 3;
// → 1
(7n + 6n - 5n) * 4n ** 3n / 2n % 3n;
// → 1n

Unary -be used to indicate a negative value BigInt, for example -42n. Unary is +not supported because it violates the asm.js code, which expects to +xalways return either Numberor an exception.

An important point - in operations you can not mix BigIntand Number. This is good because any implicit conversion can lead to loss of information. Consider an example:

BigInt(Number.MAX_SAFE_INTEGER) + 2.5;
// → ??

What should the result be equal to? There is no right answer. BigIntcannot contain fractional numbers, but Numbercannot accurately contain large numbers greater than the safe integer limit. Therefore, operations with BigIntand Numberlead to an exception TypeError.

The only exceptions to this rule are comparison operators, such as ===(discussed earlier), <and >=since they return booleans that do not carry the risk of loss of precision.

1 + 1n;
// → TypeError
123 < 124n;
// → true

Note: since BigIntthey Numberusually do not mix, do not rewrite existing code from Numberto BigInt. Decide which of these two types you need and use it. For newer APIs that work with potentially large integers, BigInta better choice. However, Numberas before, it can be used for values that are guaranteed to be in a safe range of integers.

It is also worth noting that an operator >>>that performs an unsigned right shift does not make sense for numbers BigInt, since they always contain a sign. Therefore, it >>>does not work for numbers BigInt.

API

Several new API methods have become available for BigInt.

A global constructor BigIntis similar to a constructor Number: it converts its argument to BigInt(as mentioned earlier). If the conversion fails, an exception will be thrown SyntaxErroror RangeError.

BigInt(123);
// → 123n
BigInt(1.5);
// → RangeError
BigInt('1.5');
// → SyntaxError

There are two functions that allow you to limit values to a BigIntspecified number of significant bits, while considering the number as either signed or unsigned. BigInt.asIntN(width, value)limits the valuetype number to the BigIntspecified widthnumber of bits, taking into account the sign, and BigInt.asUintN(width, value)does the same, considering the value as unsigned. For example, if you need operations on 64-bit numbers, you can use these APIs to stay in the appropriate range:

// максимально возможное значение типа `BigInt`,
// которое может быть представлено как знаковое 64-битное целое число.
const max = 2n ** (64n - 1n) - 1n;
BigInt.asIntN(64, max);
// → 9223372036854775807n
BigInt.asIntN(64, max + 1n);
// → -9223372036854775808n
//   ^ значение отрицательное, так как произошло переполнение

Note that overflow occurs as soon as we pass in a type value BigIntthat exceeds the 64-bit integer range (i.e. 63 bits for the value itself and 1 bit for the character).

BigIntallows you to accurately represent 64-bit signed and unsigned integers that are commonly used in other programming languages. Two new typed arrays, BigInt64Arrayand BigUint64Array, simplify the work with such values:

const view = new BigInt64Array(4);
// → [0n, 0n, 0n, 0n]
view.length;
// → 4
view[0];
// → 0n
view[0] = 42n;
view[0];
// → 42n

BigInt64Array ensures that its values are within the range of possible 64-bit signed values.

// максимально возможное значение типа `BigInt`,
// которое может быть представлено как знаковое 64-битное целое число.
const max = 2n ** (64n - 1n) - 1n;
view[0] = max;
view[0];
// → 9_223_372_036_854_775_807n
view[0] = max + 1n;
view[0];
// → -9_223_372_036_854_775_808n
//   ^ значение отрицательное, так как произошло переполнение

BigUint64Array works the same for unsigned 64-bit values.

Have fun with BigInt!

Tags: