How to use trams to make it easier for taxi drivers to find you
In continuation of the discussion around the article on the method of improving positioning accuracy developed by Uber, I would like to share about the research conducted in my small company and talk about the technology with which we are trying to solve a similar problem. I must say right away that there will be no mathematical calculations and deep technical details, I will try to make all the explanations as accessible as possible in the language. If it became interesting to know, and where do the trams themselves, then I ask for a cat.
So, I think no one will have any problems imagining that we are all surrounded by countless mobile devices - smartphones, tablet computers, GPS trackers, car navigators and even on-board computers in cars. Usually in
such devices are integrated receivers of global satellite navigation systems (GPS, GLONASS, Baidu). These receivers are quite budgetary and, unlike expensive professional equipment, do not support the differential mode, in which they could receive a correction correction and thus determine the location of the device with centimeter accuracy. The accuracy of determining the coordinates, unfortunately, leaves much to be desired.
But before we get to the core of our technology, let's remind ourselves of the causes of positioning errors. In real conditions, many factors influence the accuracy of determining the coordinates of a device. However, all sources of occurrence of calculation errors can be divided into the following groups according to their origin:
And now, I ask you to pay attention to a key point, which is essentially a theoretical justification for the method described below - the first three groups of error sources are common (i.e., correlated) for devices located at the same time at a relatively close distance from each other. Only errors associated with the internal noise of the device and multipath signal propagation are individual. By the way, this very idea underlies the operation of differential subsystems. In areas of the so-called spatio-temporal correlation of errors, the error parameters calculated at an arbitrary point can be used during the correlation time to correct measurements at other points in the region.
To make it more clear what is a single space-time domain and what is not, I will give examples. Consumers located simultaneously in Moscow on Leningradsky Prospekt and Entuziastov Highway will be in such a single area - the navigation field, that is, the composition and location of satellites in the sky, and the state of the ionosphere and troposphere above them will be approximately the same, since the distance between them will be substantially less distance to satellites and sizes of inhomogeneities in the ionosphere. In turn, consumers from Moscow and Kazan will be located in different spatio-temporal regions, since positioning errors will depend on different sections of the troposphere and ionosphere. And even if you are in the same place, but take measurements with a time interval of 1 or 2 hours, your measurements will correspond to different areas, since during this time there are changes not only in the ionosphere and troposphere, but also the navigation field itself changes. I note that for various variants of differential subsystems, the typical spatial dimensions of such regions range from several units to hundreds of kilometers.
After a brief review of the theoretical justification of the method, let us turn to the description of the hypothesis regarding how many “simple” devices located in a single space-time domain can help improve the accuracy of positioning of each of them.
Let's take two trams (let there be, conditionally, 43 and 56 routes) with receivers of satellite navigation systems installed on them. Let tram 43 at a given moment move from south to north, and tram 56 from west to east. At the same time, or with some slight time difference, a mark with coordinates about the current location of the trams arrives. But, since differential subsystems are not used in their devices, the accuracy of determination is not high enough for accurate positioning - the marks, most likely, in both cases will be located outside the tram rails.
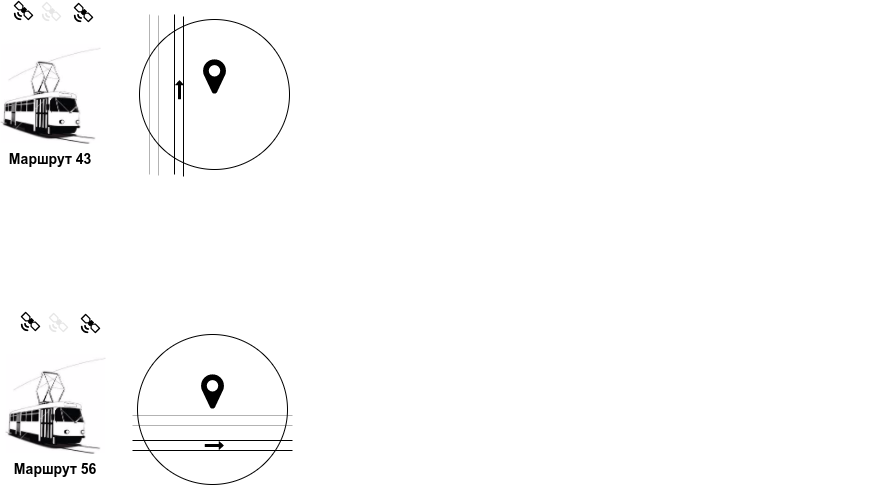
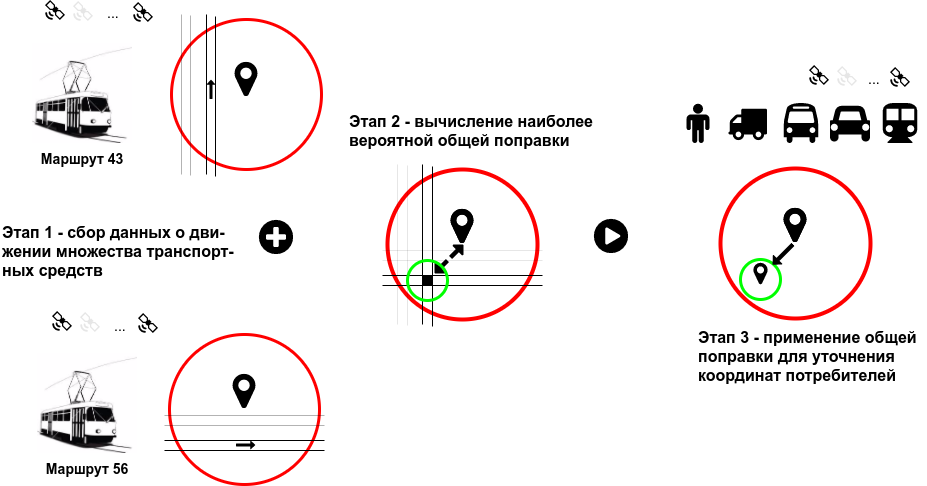
But we know that the receivers are located on trams whose physical position is imposed on the actual position in space. In fact, the variability of the position of the trams is determined by the location of the rails - the actual position of the tram of route 43 is located west of the observation mark, and tram 56, in turn, is south. Now let’s imagine a fortunate combination of circumstances that in the procedure for calculating the location in both cases the same navigation satellites (the so-called working constellation) were used. And to simplify, we assume that the accuracy of the determination was the same - the radii of the depicted circles coincide. Let's mentally combine these circles into one and find a virtual point at the intersection of two paths.

Applying this correction vector to the marks, we easily calculate the position of both trams with greater accuracy relative to the initial one. Of course, there will remain measurement errors associated with the reflection of radio signals or the error of the receivers.
And now let's take not two trams, but tens, hundreds of thousands and even millions. And not just trams, but all kinds of vehicles traveling on our roads with navigators and ERA-GLONASS devices on board. And here is the following thought that I would like to convey is this: a car on the road is a 95% tram. In the sense that all cars in the aggregate do not move randomly along the roads. If you carefully look at the flow of cars on a straight stretch of road, you will notice that most of the time they drive in lanes, as if tied to invisible rails. Only a small fraction of the time is occupied by rebuilding, overtaking and other maneuvers. In addition, unlike a pedestrian, the actual location of the vehicle is limited to a relatively small area of space - carriageways, the total area of which in large cities does not exceed 1-5% of the total territory. A car moving at a speed of more than 20-30 kilometers per hour cannot suddenly find itself outside the carriageway (on the sidewalk, lawn or in an open field, etc.) and continue to move there at the same or higher speed. And on the road with a dividing fence, the probability of leaving the oncoming lane is negligible.
Thus, it can be assumed that the coordinates of vehicles recorded using satellite navigation systems outside the “permitted” areas, that is, contradicting the existing elements of the road infrastructure, are a good information signal when calculating the correction that corrects these measurements in the direction of the real location of objects. However, not all observations will be useful. For example, the mark from a car moving in the middle lane along the Moscow Ring Road contains very little information, since all potential points within a radius of 5-6 meters are quite acceptable (a car can actually go in adjacent lanes or change lanes from one row to another). On the other hand, a car mark on a single-lane forest road will provide much more information.
You can more clearly understand the essence of the method with the help of ordinary paper large-scale maps and transparent paper. Mentally put the transparency on the map and mark the vehicles so that they correspond to the observations. The more grades, the better. Then it is necessary to move the transparency left-right and up-down by different offset values so that the maximum number of points fall into "their" sections of the road (were not in the oncoming lane, curb, etc.). Solving the optimization problem in this way, we find the most likely real location of these cars, simultaneously identifying potential violators from among those whose marks after such painstaking work fell into the “forbidden” areas for them.
This is the essence of our method - using computer calculations, without the use of additional expensive equipment, analyze a large number of observations from the same space-time domain, select a piece of the necessary information from each observation, comparing the mark with the “map” and calculate the general correction correction which can be used for all devices in this area.
To calculate the general correction corrections, it is necessary to use the most detailed digital marking of as many sections of the road network as possible, with which you can more accurately localize the real situation of consumers. And not only the drivers of vehicles themselves, but also “horseless” pedestrians, including, of course, potential taxi customers. Pedestrian devices should, of course, be excluded from the analysis and calculation of correctional corrections, but the calculated corrections can be applied to them on an equal footing with motorists.
But what is digital markup? We ourselves define it as a mathematical model that describes the actual location of some elements of the road infrastructure in space with the accuracy necessary and sufficient to solve various kinds of navigation problems. Such elements of road infrastructure include curbs, dividing lanes, road markings, tram rails, etc. Simply put, digital markings should tell you by coordinates (latitude and longitude) what this point corresponds to and how far it is from other elements of the road. For example, how close is the point to the curb, does it belong to the oncoming lane or the pedestrian sidewalk, etc.
It seems that the more accurately you can create digital markup, the more accurately you can make predictions. Unfortunately, creating accurate digital markup is an extremely difficult and expensive task. However, its presence is important for the development of unmanned vehicles, so its appearance sooner or later, I hope, will become inevitable. As part of the creation of the technology described above, we study and explore approaches based on the same principles of cooperative observations and aimed at solving this problem, but this is a slightly different story ...
So, I think no one will have any problems imagining that we are all surrounded by countless mobile devices - smartphones, tablet computers, GPS trackers, car navigators and even on-board computers in cars. Usually in
such devices are integrated receivers of global satellite navigation systems (GPS, GLONASS, Baidu). These receivers are quite budgetary and, unlike expensive professional equipment, do not support the differential mode, in which they could receive a correction correction and thus determine the location of the device with centimeter accuracy. The accuracy of determining the coordinates, unfortunately, leaves much to be desired.
But before we get to the core of our technology, let's remind ourselves of the causes of positioning errors. In real conditions, many factors influence the accuracy of determining the coordinates of a device. However, all sources of occurrence of calculation errors can be divided into the following groups according to their origin:
- Introduced by the control and measuring complex. This includes errors due to a slight discrepancy between the time scales of navigation satellites and errors due to inaccurate calculation of their locations relative to real orbits at the time of the emission of the radio signal to all consumers.
- Introduced by the equipment of the navigation satellites themselves .
- Arising from the propagation of radio signals . The main source here is the refraction of radio signals in the troposphere and ionosphere of the Earth, due to the inhomogeneities existing in them, which introduce additional delays in signal propagation.
- Introduced by the consumer receiver (internal “noise” of the device).
- Multipath in the propagation of a signal (reflection from the surface of the Earth and surrounding buildings).
And now, I ask you to pay attention to a key point, which is essentially a theoretical justification for the method described below - the first three groups of error sources are common (i.e., correlated) for devices located at the same time at a relatively close distance from each other. Only errors associated with the internal noise of the device and multipath signal propagation are individual. By the way, this very idea underlies the operation of differential subsystems. In areas of the so-called spatio-temporal correlation of errors, the error parameters calculated at an arbitrary point can be used during the correlation time to correct measurements at other points in the region.
To make it more clear what is a single space-time domain and what is not, I will give examples. Consumers located simultaneously in Moscow on Leningradsky Prospekt and Entuziastov Highway will be in such a single area - the navigation field, that is, the composition and location of satellites in the sky, and the state of the ionosphere and troposphere above them will be approximately the same, since the distance between them will be substantially less distance to satellites and sizes of inhomogeneities in the ionosphere. In turn, consumers from Moscow and Kazan will be located in different spatio-temporal regions, since positioning errors will depend on different sections of the troposphere and ionosphere. And even if you are in the same place, but take measurements with a time interval of 1 or 2 hours, your measurements will correspond to different areas, since during this time there are changes not only in the ionosphere and troposphere, but also the navigation field itself changes. I note that for various variants of differential subsystems, the typical spatial dimensions of such regions range from several units to hundreds of kilometers.
After a brief review of the theoretical justification of the method, let us turn to the description of the hypothesis regarding how many “simple” devices located in a single space-time domain can help improve the accuracy of positioning of each of them.
Let's take two trams (let there be, conditionally, 43 and 56 routes) with receivers of satellite navigation systems installed on them. Let tram 43 at a given moment move from south to north, and tram 56 from west to east. At the same time, or with some slight time difference, a mark with coordinates about the current location of the trams arrives. But, since differential subsystems are not used in their devices, the accuracy of determination is not high enough for accurate positioning - the marks, most likely, in both cases will be located outside the tram rails.

But we know that the receivers are located on trams whose physical position is imposed on the actual position in space. In fact, the variability of the position of the trams is determined by the location of the rails - the actual position of the tram of route 43 is located west of the observation mark, and tram 56, in turn, is south. Now let’s imagine a fortunate combination of circumstances that in the procedure for calculating the location in both cases the same navigation satellites (the so-called working constellation) were used. And to simplify, we assume that the accuracy of the determination was the same - the radii of the depicted circles coincide. Let's mentally combine these circles into one and find a virtual point at the intersection of two paths.

Applying this correction vector to the marks, we easily calculate the position of both trams with greater accuracy relative to the initial one. Of course, there will remain measurement errors associated with the reflection of radio signals or the error of the receivers.

And now let's take not two trams, but tens, hundreds of thousands and even millions. And not just trams, but all kinds of vehicles traveling on our roads with navigators and ERA-GLONASS devices on board. And here is the following thought that I would like to convey is this: a car on the road is a 95% tram. In the sense that all cars in the aggregate do not move randomly along the roads. If you carefully look at the flow of cars on a straight stretch of road, you will notice that most of the time they drive in lanes, as if tied to invisible rails. Only a small fraction of the time is occupied by rebuilding, overtaking and other maneuvers. In addition, unlike a pedestrian, the actual location of the vehicle is limited to a relatively small area of space - carriageways, the total area of which in large cities does not exceed 1-5% of the total territory. A car moving at a speed of more than 20-30 kilometers per hour cannot suddenly find itself outside the carriageway (on the sidewalk, lawn or in an open field, etc.) and continue to move there at the same or higher speed. And on the road with a dividing fence, the probability of leaving the oncoming lane is negligible.
Thus, it can be assumed that the coordinates of vehicles recorded using satellite navigation systems outside the “permitted” areas, that is, contradicting the existing elements of the road infrastructure, are a good information signal when calculating the correction that corrects these measurements in the direction of the real location of objects. However, not all observations will be useful. For example, the mark from a car moving in the middle lane along the Moscow Ring Road contains very little information, since all potential points within a radius of 5-6 meters are quite acceptable (a car can actually go in adjacent lanes or change lanes from one row to another). On the other hand, a car mark on a single-lane forest road will provide much more information.
You can more clearly understand the essence of the method with the help of ordinary paper large-scale maps and transparent paper. Mentally put the transparency on the map and mark the vehicles so that they correspond to the observations. The more grades, the better. Then it is necessary to move the transparency left-right and up-down by different offset values so that the maximum number of points fall into "their" sections of the road (were not in the oncoming lane, curb, etc.). Solving the optimization problem in this way, we find the most likely real location of these cars, simultaneously identifying potential violators from among those whose marks after such painstaking work fell into the “forbidden” areas for them.
This is the essence of our method - using computer calculations, without the use of additional expensive equipment, analyze a large number of observations from the same space-time domain, select a piece of the necessary information from each observation, comparing the mark with the “map” and calculate the general correction correction which can be used for all devices in this area.
To calculate the general correction corrections, it is necessary to use the most detailed digital marking of as many sections of the road network as possible, with which you can more accurately localize the real situation of consumers. And not only the drivers of vehicles themselves, but also “horseless” pedestrians, including, of course, potential taxi customers. Pedestrian devices should, of course, be excluded from the analysis and calculation of correctional corrections, but the calculated corrections can be applied to them on an equal footing with motorists.
But what is digital markup? We ourselves define it as a mathematical model that describes the actual location of some elements of the road infrastructure in space with the accuracy necessary and sufficient to solve various kinds of navigation problems. Such elements of road infrastructure include curbs, dividing lanes, road markings, tram rails, etc. Simply put, digital markings should tell you by coordinates (latitude and longitude) what this point corresponds to and how far it is from other elements of the road. For example, how close is the point to the curb, does it belong to the oncoming lane or the pedestrian sidewalk, etc.
It seems that the more accurately you can create digital markup, the more accurately you can make predictions. Unfortunately, creating accurate digital markup is an extremely difficult and expensive task. However, its presence is important for the development of unmanned vehicles, so its appearance sooner or later, I hope, will become inevitable. As part of the creation of the technology described above, we study and explore approaches based on the same principles of cooperative observations and aimed at solving this problem, but this is a slightly different story ...
