How to create a neural network in just 30 lines of JavaScript code

Translation of How to create a Neural Network in JavaScript in only 30 lines of code .

In this article, we will look at how you can create and train a neural network using the Synaptic.js library , which allows you to conduct deep training in conjunction with Node.js browser. Let's create a simple neural network that solves the XOR equation . You can also study a specially written interactive tutorial .



But before moving on to the code, let's talk about the basics of neural networks.

Neurons and synapses

The main "building" element of the neural network, of course, is a neuron . Like a function, it takes several input values ​​and produces some kind of result. There are different types of neurons. Our network will use sigmoids that take any numbers and reduce them to values ​​in the range from 0 to 1. The principle of action of such a neuron is illustrated below. At the input, it has the number 5, and at the output 1. The arrows indicate the synapses that connect the neuron to other layers of the neural network.



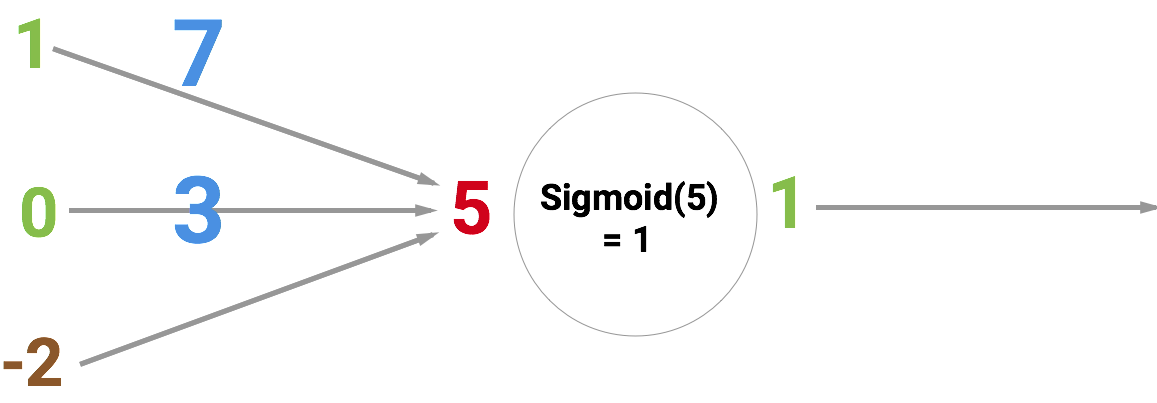
But why is the number 5 at the entrance? This is the sum of the three synapses that “enter” the neuron. Let's figure it out.

On the left we see the values ​​1 and 0, as well as an offset of -2. First, the first two values ​​are multiplied by their weights., which are equal to 7 and 3, the results are added up and the bias is added to them, we get 5. This will be the input value for our artificial neuron.



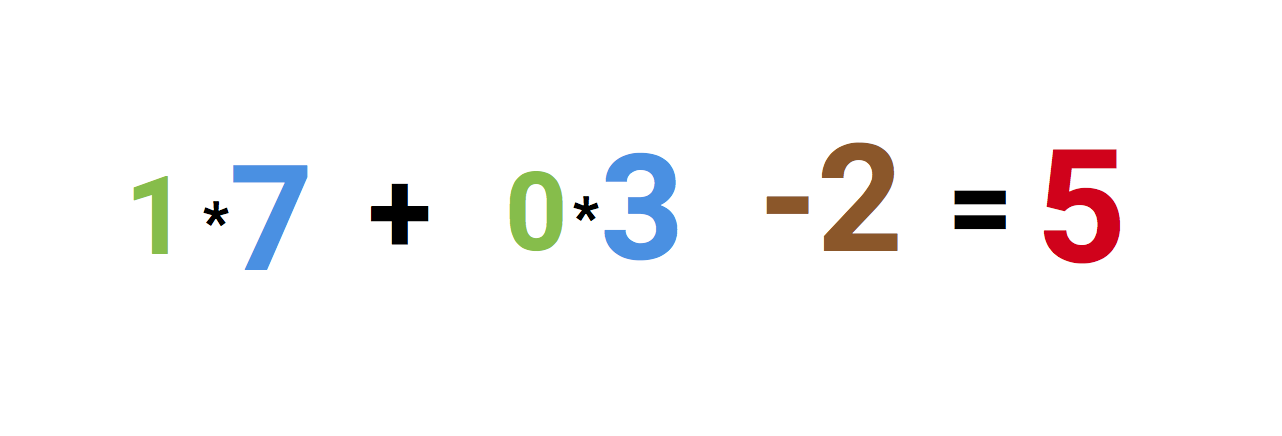
And since this is a sigmoid that reduces any value to a range from 0 to 1, the output value will be 1. If you connect these neurons to each other using synapses, you get a neural network through which the values ​​pass from input to output and are transformed. Something like this: A



neural network learns to generalize in order to solve all sorts of tasks, for example, handwriting recognition or mail spam. And the ability to generalize well depends on the choice of the correct weights and displacements within the entire neural network.

For training, you simply give a set of samples and force the neural network to process them over and over again until it gives the correct answer. After each iteration, the prediction accuracy is calculated and the weights and offsets are adjusted so that the next time the response of the neural network is slightly more accurate. This learning process is called backpropagation. If you spend thousands of iterations, then your neural network will learn to generalize well.

We will not consider the work of the method of back propagation of error; this is beyond the scope of our manual. But if you are interested in the details, then you can read these articles:

• A Step by Step Backpropagation Example
• Hackers Guide to Neural Nets
• NeuralNetworksAndDeepLarning

The code

First, create the layers, and do it in synaptic mode using the function new Layer(). The number passed to it means the number of neurons in the fresh layer. If you don’t know what a layer is , then check out the above tutorial .

const { Layer, Network } = window.synaptic;
var inputLayer = new Layer(2);
var hiddenLayer = new Layer(3);
var outputLayer = new Layer(1);

Now connect the layers to each other and instantiate a new network.

inputLayer.project(hiddenLayer);
hiddenLayer.project(outputLayer);
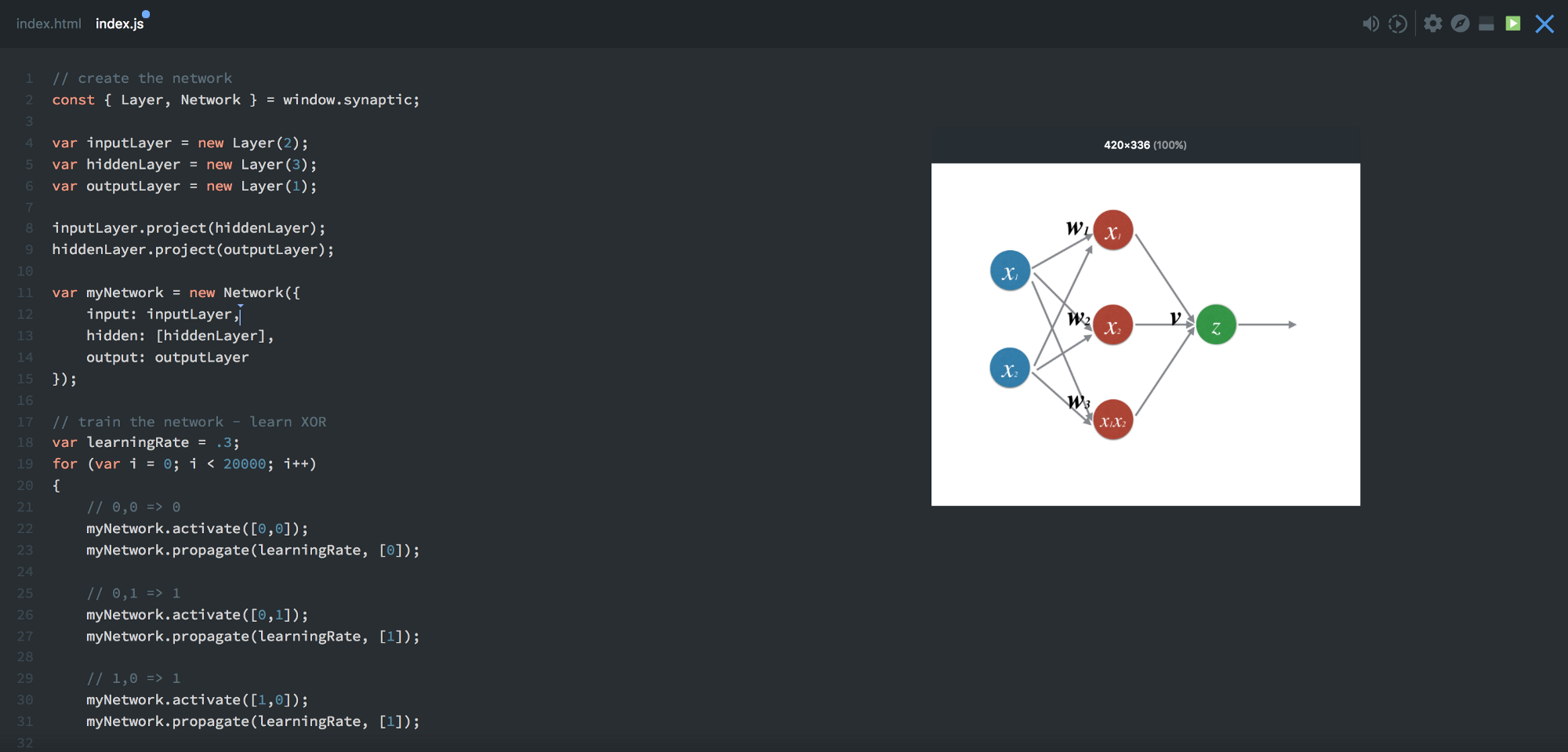
var myNetwork = new Network({
 input: inputLayer,
 hidden: [hiddenLayer],
 output: outputLayer
});

We got a network according to the scheme 2-3–1, which looks like this:



Let's train it:

// train the network - learn XOR
var learningRate = .3;
for (var i = 0; i < 20000; i++) {
  // 0,0 => 0
  myNetwork.activate([0,0]);
  myNetwork.propagate(learningRate, [0]);
  // 0,1 => 1
  myNetwork.activate([0,1]);
  myNetwork.propagate(learningRate, [1]);
  // 1,0 => 1
  myNetwork.activate([1,0]);
  myNetwork.propagate(learningRate, [1]);
  // 1,1 => 0
  myNetwork.activate([1,1]);
  myNetwork.propagate(learningRate, [0]);
}

We drove 20,000 training iterations. In each iteration data four times as are run back and forth, i.e. are input four possible combinations of values: [0,0] [0,1] [1,0] [1,1].

Let's start with the execution myNetwork.activate([0,0]), where [0,0]is the input. This is called forward propagation, or neural network activation . After each direct propagation, you need to do the opposite, in which the neural network updates its weights and displacements.

Backpropagation is performed with myNetwork.propagate(learningRate, [0]), where learningRate is a constant, which means how much weights need to be adjusted each time. The second parameter 0is the correct output value at the input [0,0].

Next, the neural network compares the resulting output value with the correct one. Thus, she determines the accuracy of her own work.

According to the results of the comparison, the neural network adjusts weights and biases, so that next time it will answer a little more accurately. After 20,000 such cycles, you can check how well our neural network has trained, activating it using all four possible input values:

console.log(myNetwork.activate([0,0])); 
-> [0.015020775950893527]
console.log(myNetwork.activate([0,1]));
->[0.9815816381088985]
console.log(myNetwork.activate([1,0]));
-> [0.9871822457132193]
console.log(myNetwork.activate([1,1]));
-> [0.012950087641929467]

If we round the results to the nearest integer values, we get exact answers for the XOR equation. Works!

That's all. Although we just dug up the topic of neural networks just a little bit, you can already experiment with Synaptic yourself and continue your self-study. There are many more good tutorials in the library authors wiki .