10,000 likes
At the very beginning of January, coin and I wandered through the cold and rainy streets of London and talked about technology, life, and something else. From time to time I took photos on my old Canon EOS 400D, and at some point my friend said: “Here you take pictures, take pictures, and nobody likes your photos.” I did not find what to answer, but when I returned home, I created an account in one of the social networks where you can post and like photos, and made a plan: to get 10,000 followers in 100 days and by the end of this period get 500 likes for the post. After that, he selected a couple of hundreds of interesting photos and posted the first one. And only a few people liked her. This was not enough, it was necessary to come up with some method.

To increase the number of subscribers, you need to be noticed. You can do this in many different ways, but the easiest and most working one is to subscribe to someone and enjoy his photos in the hope that the person will do the same in return. It is not thoughtless to do this for two reasons: it is very similar to spam, and there is a limit to the number of such actions. Therefore, it was necessary to figure out how to follow only those who are likely to sign in response.
At first I randomly signed up for two to three thousand people, after that I wrote down the three numbers that are in the user profile in the table: the number of posts N p , the number of subscriptions N f and the number of subscribers N fd . To the last column MI entered information on the table about whether the user subscribed to me in response or not.
The following seemed plausible.
Visualization experiments have shown that everything looks better in logarithmic coordinates. Although the point clouds intersect strongly, you can build some sort of classifier and see what happens.

Using the support vector method, I obtained the following linear classifier, which is consistent with what was expected:
–0.19 log N fd + 0.42 log N f - 0.18 log N p > 0.57.
After that, things went more fun: 20 percent more subscribed to me back, that is, approximately every fourth to fifth. But this is not the result that I wanted. It was necessary to come up with something better.
In addition to the above three numbers, I did not want to waste time extracting any other information, so I wondered what would happen if I looked again at these parameters, but in three days.
Having again typed the data, I began to play with different combinations of these values. And it turned out that a very good result can be achieved by adding only one factor - by how much the number of subscriptions for the account has increased. It turns out that the more people follow people in three days, the greater the chance that he will follow me.
Here, too, everything is better with logarithms, so the new factor in the result looks like this: the log + ( of N ' f - of N f ), where the difference of N' f - of N f - this is the change in the number of subscriptions in three days,

This function avoids the problems with logarithm of negative values. Also, people whose number of subscriptions decreases is probably not interesting to us.
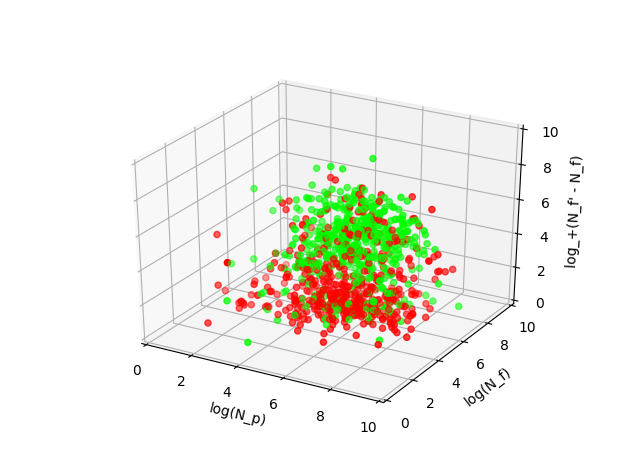
The support vector method gives the following linear classifier:
–0.06 log N fd + 0.17 log N f - 0.10 log N p + 0.16 log + ( N ' f - N f )> 0.55.
Since it’s a mistake when we don’t subscribe to the person who would follow us, we are not particularly interested, we can slightly increase the right side of the inequality in order to further improve the result. As a result, approximately every second subscribed to me back.
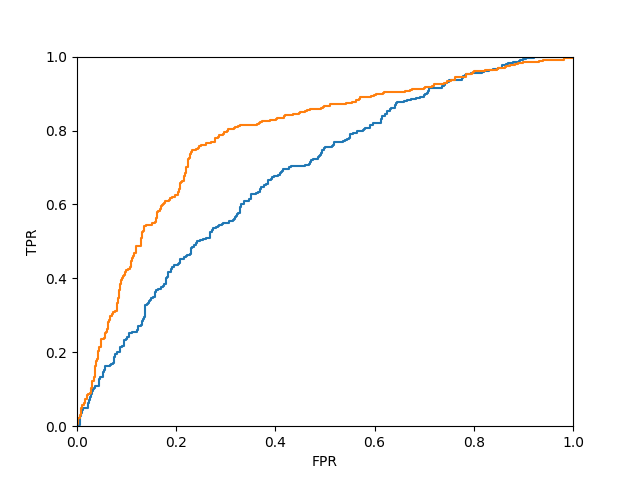
Below are the ROC curves for the two resulting classifiers.
After 87 days, having gained 10,000 subscribers, I stopped. The average likes of the last 15 posts turned out to be 490, which is almost equal to the number I was aiming for. Considering that I maximized the number of subscribers, rather than the number of likes, I think this result is not bad, especially since it is close to the average value for such an account.
The fourth factor turned out to be the most interesting for me in this experiment - the change in the number of subscriptions in three days. It turned out to be very simple and at the same time unexpectedly very significant.

To increase the number of subscribers, you need to be noticed. You can do this in many different ways, but the easiest and most working one is to subscribe to someone and enjoy his photos in the hope that the person will do the same in return. It is not thoughtless to do this for two reasons: it is very similar to spam, and there is a limit to the number of such actions. Therefore, it was necessary to figure out how to follow only those who are likely to sign in response.
At first I randomly signed up for two to three thousand people, after that I wrote down the three numbers that are in the user profile in the table: the number of posts N p , the number of subscriptions N f and the number of subscribers N fd . To the last column MI entered information on the table about whether the user subscribed to me in response or not.
The following seemed plausible.
- The more people a person has, the sooner the user will follow me.
- The greater the ratio of the number of subscriptions to the number of posts, the sooner the user will subscribe to me. (Since the more posts, the older the account. And if the account is created long ago, and there are few subscriptions, then the user is not interested in subscribing to others.)
- The greater the ratio of the number of subscriptions to the number of subscribers, the sooner the user will subscribe to me. (Observation shows that this number is small for shops, bots, famous personalities, etc., and close to 1 for ordinary people.)
Visualization experiments have shown that everything looks better in logarithmic coordinates. Although the point clouds intersect strongly, you can build some sort of classifier and see what happens.

Using the support vector method, I obtained the following linear classifier, which is consistent with what was expected:
–0.19 log N fd + 0.42 log N f - 0.18 log N p > 0.57.
After that, things went more fun: 20 percent more subscribed to me back, that is, approximately every fourth to fifth. But this is not the result that I wanted. It was necessary to come up with something better.
In addition to the above three numbers, I did not want to waste time extracting any other information, so I wondered what would happen if I looked again at these parameters, but in three days.
Having again typed the data, I began to play with different combinations of these values. And it turned out that a very good result can be achieved by adding only one factor - by how much the number of subscriptions for the account has increased. It turns out that the more people follow people in three days, the greater the chance that he will follow me.
Here, too, everything is better with logarithms, so the new factor in the result looks like this: the log + ( of N ' f - of N f ), where the difference of N' f - of N f - this is the change in the number of subscriptions in three days,
This function avoids the problems with logarithm of negative values. Also, people whose number of subscriptions decreases is probably not interesting to us.

The support vector method gives the following linear classifier:
–0.06 log N fd + 0.17 log N f - 0.10 log N p + 0.16 log + ( N ' f - N f )> 0.55.
Since it’s a mistake when we don’t subscribe to the person who would follow us, we are not particularly interested, we can slightly increase the right side of the inequality in order to further improve the result. As a result, approximately every second subscribed to me back.
Below are the ROC curves for the two resulting classifiers.

After 87 days, having gained 10,000 subscribers, I stopped. The average likes of the last 15 posts turned out to be 490, which is almost equal to the number I was aiming for. Considering that I maximized the number of subscribers, rather than the number of likes, I think this result is not bad, especially since it is close to the average value for such an account.
The fourth factor turned out to be the most interesting for me in this experiment - the change in the number of subscriptions in three days. It turned out to be very simple and at the same time unexpectedly very significant.
