Global lighting using voxel cone tracing
In this article, I will talk about the implementation of one of the algorithms for calculating global (reflected) lighting used in some games and other products - Voxel Cone Tracing (VCT). Perhaps someone read an old article ([VCT]) of 2011 or watched a video . But the article does not give comprehensive answers to questions about how to implement one or another stage of the algorithm.


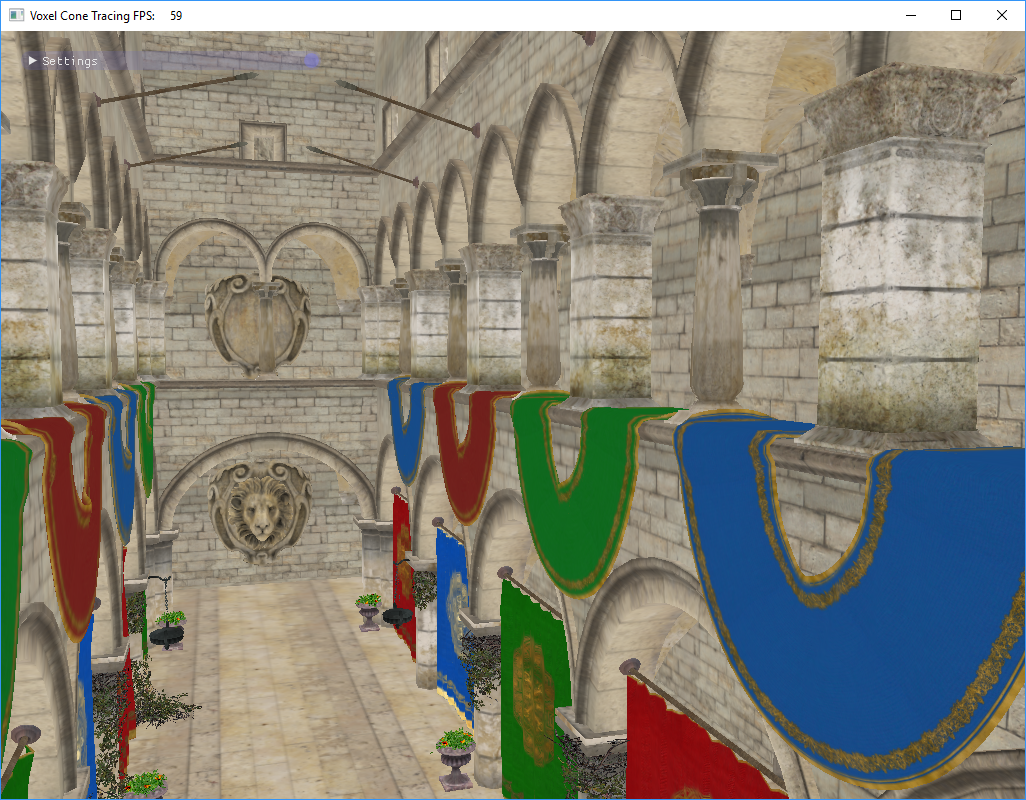
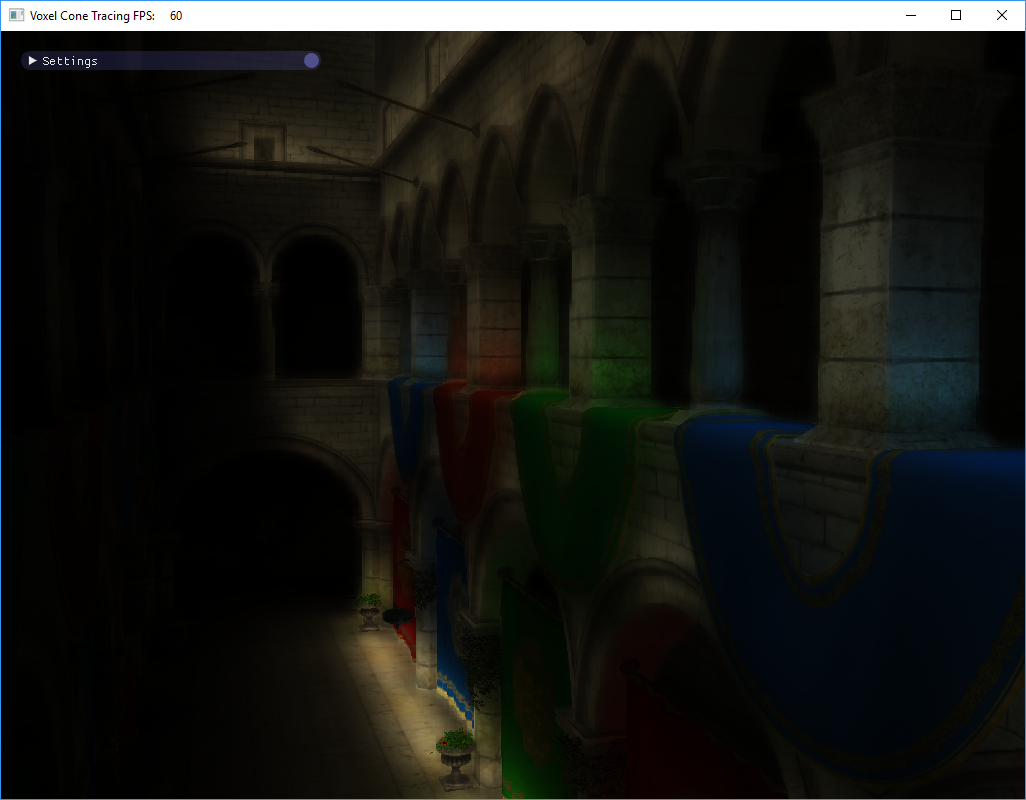
Rendering a scene without global lighting, and using VCT:
First of all, it is worth saying that implementing global lighting using environment maps (PMREM / IBL) is cheaper than VCT. For example, one of the UE4 developers spoke in a podcast(1:34:05 - 1:37:50) that they rendered the demo using VCT, and then using environment maps, and the picture turned out to be about the same. Nevertheless, research is underway within the framework of this approach. For example, the modern VXGI from Nvidia is based on his ideas.
During the work, I relied on a bunch of sources that can be found at the end of the article.
To simplify the task, the implementation takes into account only diffuse lighting (Labmert's model), but it is argued that this algorithm is suitable for many other BRDFs. Also, the implementation does not take into account dynamic objects of the scene.
I will describe the implementation in terms of DirectX, but such an algorithm can also be implemented on OpenGL. Some DX 11.1 chips are used in the work (for example, using UAV in a vertex shader), but you can do without them, thereby lowering the minimum system requirements for this algorithm.
For a better understanding of the operation of the algorithm, we describe its general stages, and then we detail each of them. The most common parts of the algorithm:
These stages may have several ideological options for implementations or contain additional optimizations. I want to show in a general way how this can be done.
First, let's determine the storage structure of the voxelized scene. You can voxelize all objects into a 3D texture. The disadvantage of this solution is the non-optimal memory consumption, because most of the scene is empty space. For voxelization with a resolution of 256x256x256 of the R8G8B8A8 format, such a texture will occupy 64 MB, and this without taking into account the mips. Such textures are required for color and surface normals, as well as for baked lighting.
To optimize memory consumption, data packing algorithms are used. In our implementation, we will use Sparse Voxel Octree (SVO), as in the original article. But there are other algorithms, for example, 3D Clipmap [S4552].
SVO is a sparse octree of a scene. Each node of such a tree divides the subspace of the scene into 8 equal parts. A sparse tree does not store information about space that is not occupied by anything. We will use this structure to search for voxels by their coordinates in space, as well as to sample baked lighting. Baked lighting will be stored in a special 3D texture - a block buffer, which we will talk about below.
We consider each of the stages of the algorithm separately.

We will store the voxelized scene as an array of voxels. On the GPU, this array is implemented through StructuredBuffer / RWStructuredBuffer. The structure of the voxels will be as follows:
For compact storage of the scene, we use SVO. The tree will be stored in a R32_UINT 2D texture. Tree node structure:

Schematic representation of SVO nodes [DP]
In the SVO leaves at the last level, the indices of the corresponding voxels from this array will be stored.
Let's say the resolution of our scene is 256x256x256, then to store a completely filled tree we need a texture of 6185x6185 (145.9 Mb). But we do not intend to store a complete tree. According to my observations, for a Sponza scene with such a resolution of the scene, a sparse tree is placed in a texture of 2080x2080 (16.6 Mb).
To create a voxel array, you need to voxelize all the objects in the scene. Let's take advantage of the simple voxelization from the related Octree-Based Sparse Voxelization article . This technique is easy to implement and works in one GPU pass.

Pipeline voxelization object [SV]
Calculate the bounding box of the scene. Set the viewport to resolve the voxelized scene (for example, 256x256). We place the orthographic camera over the stage so as to fit the bounding cube. Render each scene object that we want to consider.
In the geometric shader, we handle the triangles of an object. Using the normal of the triangle, the axis is selected in the direction of which the projection area of this triangle is maximum. Depending on the axis, we rotate the triangle with the largest projection to the rasterizer - so we get more voxels.
In a pixel shader, each fragment will be a voxel. Create a Voxel structure with coordinates, color and normal, and add it to the voxel array.
At this stage, it is desirable to use low-poly LODs (LODs) of objects, so as not to have problems with missing voxels and with the merging of voxels of adjacent triangles (such cases are discussed in [SV]).


Voxelization artifacts - not all triangles are rasterized. Use low poly lodes or stretch triangles additionally.
When the whole scene is voxelized, we have an array of voxels with their coordinates. From this array, you can build SVO, with which we can find voxels in space. Initially, each pixel of a texture with SVO is initialized to 0xffffffff. To write tree nodes through a shader, the SVO texture will be represented as a UAV resource (RWTexture2D). To work with the tree, we will start an atomic node counter (D3D11_BUFFER_UAV_FLAG_COUNTER).
Let us describe in stages the algorithm for creating an octree. Under the node address in SVO, we further mean the index of the node, which is converted to the 2D coordinates of the texture. Further, allocation of a node means the following set of actions:
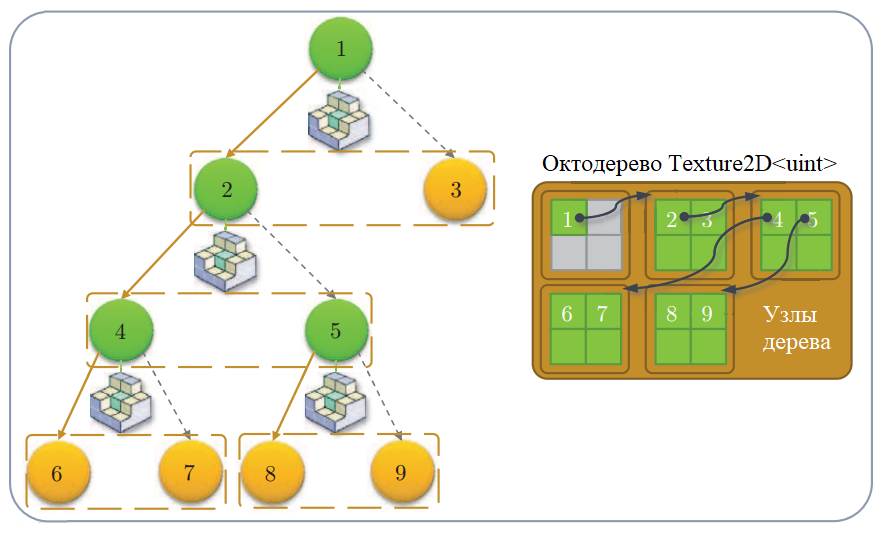
Schematic representation of the octree and its representation in the texture [SV]
An algorithm for creating an octree with a height N is as follows:
Having built such an octree tree, we can easily find the voxel of the scene by the coordinates in space, going down the SVO.
Now that we have constructed the octree of the voxelized scene, we can use this information to preserve the illumination reflected by the voxels from the light sources. Illumination is saved in the 3D texture of the R8G8B8A8 format. This will allow us to use trilinear interpolation of the GPU when sampling the texture, and as a result we get a smoother final image. This texture is called a brick buffer, because it consists of blocks arranged according to SVO. A block is another representation of a group of voxels in space.
Groups of 2x2x2 voxels whose indices are located in the leaves of SVO are displayed on 3x3x3 voxel blocks from 3D texture:
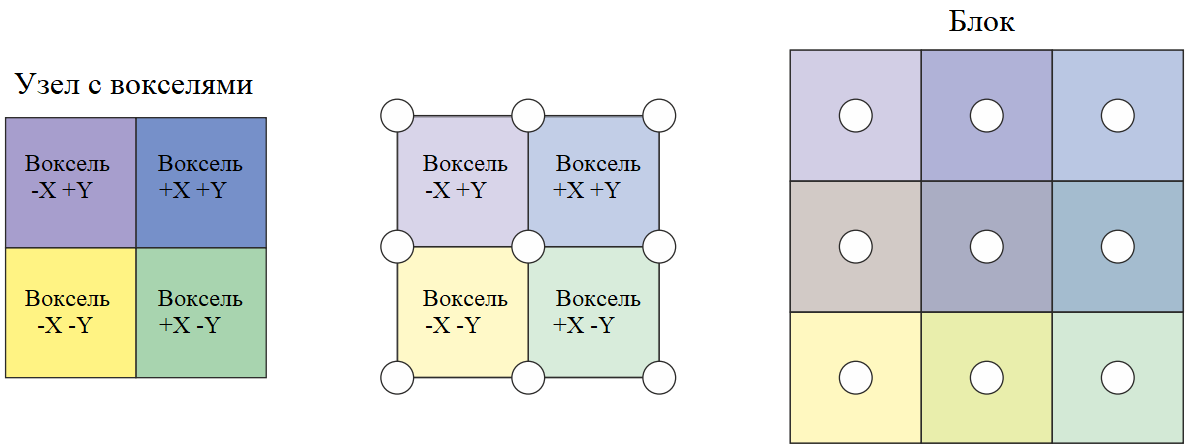
Mapping a group of voxels into a voxel block [DP]
Groups of voxels located next to each other in the scene can be scattered in the texture (since the texture is based on SVO). Therefore, for the correct interpolation between neighboring groups of voxels, it is necessary to do additional work on averaging the values between neighboring blocks.

Averaging the boundaries of neighboring blocks
Voxels from a block are located at the corners of the initial group of voxels and between them. Thus, blocks occupy more space in space than the original voxels. But sampling inside the block will be performed along the boundaries of the original voxels. So there is a likeness of some delimiter half a pixel wide, which is not used in any way.
Blocks arranged according to SVO leaves are a display of the original voxels. Blocks located in accordance with other SVO nodes at certain levels of the octree are MIP levels of the block buffer.

Schematic representation of the octree tree, its representation in the texture and mapping of the blocks to the buffer [SV]
At the same time, the blocks do not have to be 3x3x3, they can be 2x2x2, and 5x5x5 is a matter of accuracy of the representation. 2x2x2 blocks would be another good way to save memory, but I have never seen such an approach.

Comparison of interpolation when sampling four neighboring voxels: without a block buffer, from a block buffer of 3x3x3 and from a buffer of blocks 5x5x5
Creating such a block buffer is a rather time-consuming task. We will create two buffers: for storing scene transparency and for storing lighting.
The first step is to fill in the voxels of the blocks matched with the leaves of the octree. Suppose we compute reflected light in specific SVO voxels. Then these values will be displayed in the corresponding angular voxels of the block buffer.

After the calculation of outgoing lighting is completed, for each block we add the remaining voxels with the averaged values of the neighboring voxels inside the block:

Now average the values between the neighboring blocks. That is why neighbors in space are stored in the nodes of the tree.

One of the options for averaging the block buffer is along each axis in three passes. Possible artifacts with this averaging are marked with a red rectangle [DP]
Create the MIP levels of such a buffer. The nodes of the upper levels of SVO will be displayed in blocks that contain the averaged values from the underlying level. Each block corresponding to a node from the top level of the tree includes information from blocks of the corresponding descendants. It can also be blocks that correspond not only directly to the child nodes in the tree, but also to their neighbors (see the figure below).

On the left - the block includes information from child blocks and their neighbors. Right - a block includes information only from child blocks [DP]
To reduce the number of memory accesses, only voxels of child blocks are used for each block being calculated (figure on the right). After that, the values between neighboring blocks are averaged, as described above. And so we create the MIP levels until we get to the root node of SVO.
Let's create two buffers - a buffer of scene transparency blocks and a buffer of reflected light blocks.
The buffer of transparency blocks is preliminarily created based on the voxelized geometry of the scene. We will keep directional voxel transparency. To do this, fill in the RGB values of the voxels of the blocks from the lower level in accordance with the transparency of the voxels, and when creating the MIP levels of the blocks for each calculated voxel, we will choose the average maximum transparency value along the XYZ axes, and save them in the corresponding RGB texture values. This solution helps to take into account the blocking of light in space in a certain direction.
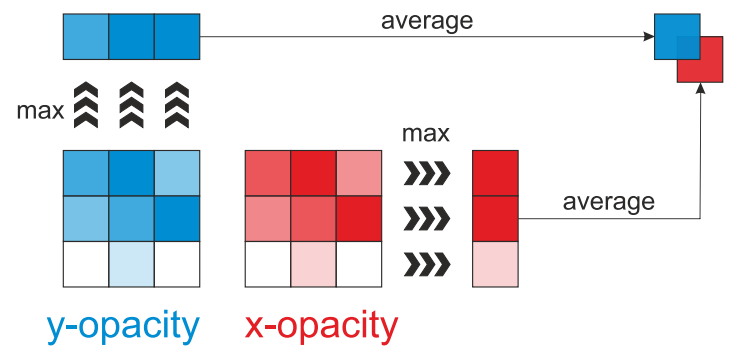
In each direction, a maximum in the transparency value is selected (i.e. 1.0 is a completely opaque object, and this value will be maximum). Further, when constructing MIP levels, the maxima along the XYZ axes in the daughter blocks are averaged and added to the RGB components. [DP]
Lighting reflected by a voxel is calculated by processing the shadow map from the calculated light sources. Using this map, we can get the coordinates of objects in space and, using SVO, transform them into indices of illuminated voxels.
Usually the resolution of the shadow map is higher than the resolution of the octree. The original article describes an approach in which each pixel in the shadow map is considered a conditional photon. Accordingly, depending on the number of photons there will be a different contribution to the illumination. In my implementation, I simplified this stage and counted the illumination only once for each voxel that fell into the shadow map.
To avoid repeated calculations, for each voxel for which the reflected lighting has already been calculated, we will use the flag bit of the octree node that stores the pointer to the voxel. Also, when processing the shadow map, among the pixels included in the same voxel, you can select only the top left one for calculation.


Fragment of the shadow map (left). On the right - the upper left pixels that are part of the same voxel are shown in red.
To calculate the reflected illumination, the standard albedo * lightColor * dot (n, l) is used, but in the general case it depends on BRDF. The calculated illumination is recorded in the buffer of the lighting units. After processing the shadow map, the block buffer is refilled and MIP levels are created, as described above.
The algorithm is quite expensive. It is necessary to recalculate the buffer of the lighting units with each change in lighting. One of the possible optimization methods is to smear a buffer update by frames .
In order to apply voxel tracing to cones for a specific pixel, you need to know the normal and location of the pixel in space. These attributes are used to bypass SVO and sample the lighting block buffer. You can get these attributes from G-buffer .
Using G-buffer, you can also calculate the reflected light at a lower resolution than the viewport, which improves performance.
When the buffer of lighting blocks is calculated, we can proceed to the calculation of lighting reflected from the scene to objects in the frame — that is, global lighting. To do this, trace voxels with cones.
For each pixel, several cones are emitted in accordance with BRDF. In the case of the Lambert lighting model, the cones are emitted uniformly in a hemisphere oriented using the normal derived from the G-buffer.

Emitting cones from the surface for which incoming lighting is calculated [VCT]
In the calculation, we assume that the illumination obtained from a point on the surface in the voxel direction will be the same as that emitted from the voxel towards the surface in a certain cone of visibility.
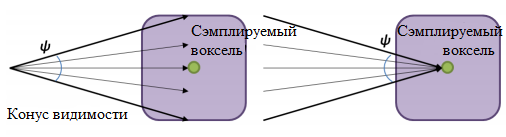
[VCT]
Tracing is done step by step. At each step, the buffer of the lighting blocks is sampled in accordance with the level of the octree tree (i.e., in accordance with the created MIP levels), starting from the lowest to the highest.

Sampling the block buffer using a cone in accordance with the SVO [DP] levels
Tracing with a cone is performed similarly to rendering volumetric objects [A]. Those. the alpha front-to-back model is used, in which at each next step along the cone, color and transparency are calculated as follows:
where a is transparency, c is the value obtained from the buffer of lighting blocks multiplied by transparency (premultiplied alpha).
The transparency value is calculated using the transparency block buffer:
In other words, transparency is read in the direction of the cone at a particular point. This is not the only approach. You can, for example, store transparency in the alpha channel of the lighting block buffer. But then the direction of the reflected light is lost. I also tried to store directional illumination in six buffers of lighting units (two for each axis) - there are more costs than visible advantages.
The final result for the cones is weighted summarized depending on the angles of the cones. If all the cones are the same, the weight is divided equally. The choice of the number of cones and the size of the solution angles is a question of the ratio of speed and quality. In my implementation, 5 cones of 60 degrees (one in the center, and 4 on the sides).
The figure above schematically shows the sampling points along the axis of the cone. It is recommended to choose the location of the samples so that the octree node from the corresponding level fits into the cone. Or you can replace it with the corresponding sphere [SB]. But then sharp voxel boundaries may appear, so the location of the samples is adjusted. In my implementation, I just move the samples closer to each other.
As a bonus to reflected light, we also get Ambient Occlusion shading , which is calculated based on the alpha value obtained during the trace. Also, when calculating AO at each step along the axis of the cone, a correction is made depending on the distance
The result is saved in the RGBA texture (RGB for lighting and A for AO). For a smoother result, a blur can be applied to the texture. The final result will depend on the BRDF. In my case, the calculated rereflection is first multiplied by the surface albedo obtained from G-buffer, then optionally multiplied by AO, and finally added to the main lighting.
In general, after certain settings and improvements, the picture is similar to the result from the article.



Comparison of results - on the left is a scene rendered in Mental Ray, on the right is Voxel Cone Tracing from the original article, in the center is my implementation.
The problem of self-lighting . Since in most cases the surface is physically located in its own voxels, it is necessary to somehow deal with self-lighting. One solution is to push the beginning of the cones in the direction of the normals. Also, this problem can theoretically be avoided if the directional distribution of lighting is stored in voxels.
Performance issue . The algorithm is quite complex, and you will have to spend a lot of time on an effective implementation on the GPU. I wrote the implementation "head-on", using fairly obvious optimizations, and the load turned out to be high. At the same time, even an optimized algorithm when searching for voxels in a tree will require a lot of SVO texture samples depending on each other.
In my implementation, I emit 5 cones, sampling block buffers for the 4 penultimate levels of the 256x256x256 octree tree. According to the Intel GPA, the relative performance distribution is as follows:

Performance distribution. G-Buffer and Shadow Map without prior cooling.
In the original article, three diffuse cones are used on a 512x512 texture throughout SVO (512x512x512 - 9 levels). Together with direct lighting, this takes ~ 45% of the frame time of 512x512. There is much to strive for. It is also necessary to pay attention to optimizing the updating of the lighting buffer.
Another problem of the algorithm is the leakage of light through objects(light leaking). This happens with thin objects that make a small contribution to the transparency block buffer. Also, planes located next to illuminated voxels of the lower levels of SVO are affected by this phenomenon:


Light leaking: on the left when using the VCT algorithm, on the right - in real life. This effect can be mitigated with AO.
From the foregoing, another consequence follows: it is not so easy to configure the algorithm to get a good picture - how many cones to take, how many SVO levels, with what coefficients, etc.
We considered only static objects in the scene. To store dynamic objects, you will need to modify the SVO and corresponding buffers. As a rule, in this case it is proposed to separately store static and dynamic nodes.
To summarize, I would not recommend this technique if you do not have enough time, patience and strength. But then it will help to achieve a plausible ambient-lighting.
Demonstration in dynamics:
Link to the application: https://github.com/Darkxiv/VoxelConeTracing (bin / VCT.exe)
List of sources and resources that can help in the implementation of voxel tracing by cones:


Rendering a scene without global lighting, and using VCT:
First of all, it is worth saying that implementing global lighting using environment maps (PMREM / IBL) is cheaper than VCT. For example, one of the UE4 developers spoke in a podcast(1:34:05 - 1:37:50) that they rendered the demo using VCT, and then using environment maps, and the picture turned out to be about the same. Nevertheless, research is underway within the framework of this approach. For example, the modern VXGI from Nvidia is based on his ideas.
During the work, I relied on a bunch of sources that can be found at the end of the article.
To simplify the task, the implementation takes into account only diffuse lighting (Labmert's model), but it is argued that this algorithm is suitable for many other BRDFs. Also, the implementation does not take into account dynamic objects of the scene.
I will describe the implementation in terms of DirectX, but such an algorithm can also be implemented on OpenGL. Some DX 11.1 chips are used in the work (for example, using UAV in a vertex shader), but you can do without them, thereby lowering the minimum system requirements for this algorithm.
For a better understanding of the operation of the algorithm, we describe its general stages, and then we detail each of them. The most common parts of the algorithm:
- Voxelization of the scene . We rasterize the scene into a set of voxels containing material properties (such as color) and surface normal.

- Reflective lighting roasting . For voxels, incoming or outgoing radiation from light sources is calculated, and the result is recorded in a 3D texture.


- Trace cones . For each calculated pixel of the surface, a group of cones is created. A cone is an abstraction that mimics a group of rays emitted to capture radiation from various types of 3D lighting textures. The final result is weighted averaged and added up with the main lighting.

These stages may have several ideological options for implementations or contain additional optimizations. I want to show in a general way how this can be done.
First, let's determine the storage structure of the voxelized scene. You can voxelize all objects into a 3D texture. The disadvantage of this solution is the non-optimal memory consumption, because most of the scene is empty space. For voxelization with a resolution of 256x256x256 of the R8G8B8A8 format, such a texture will occupy 64 MB, and this without taking into account the mips. Such textures are required for color and surface normals, as well as for baked lighting.
To optimize memory consumption, data packing algorithms are used. In our implementation, we will use Sparse Voxel Octree (SVO), as in the original article. But there are other algorithms, for example, 3D Clipmap [S4552].
SVO is a sparse octree of a scene. Each node of such a tree divides the subspace of the scene into 8 equal parts. A sparse tree does not store information about space that is not occupied by anything. We will use this structure to search for voxels by their coordinates in space, as well as to sample baked lighting. Baked lighting will be stored in a special 3D texture - a block buffer, which we will talk about below.
We consider each of the stages of the algorithm separately.
Voxelization scene

We will store the voxelized scene as an array of voxels. On the GPU, this array is implemented through StructuredBuffer / RWStructuredBuffer. The structure of the voxels will be as follows:
struct Voxel
{
uint position;
uint color;
uint normal;
uint pad; // 128 bits aligment
};For compact storage of the scene, we use SVO. The tree will be stored in a R32_UINT 2D texture. Tree node structure:

Schematic representation of SVO nodes [DP]
In the SVO leaves at the last level, the indices of the corresponding voxels from this array will be stored.
Let's say the resolution of our scene is 256x256x256, then to store a completely filled tree we need a texture of 6185x6185 (145.9 Mb). But we do not intend to store a complete tree. According to my observations, for a Sponza scene with such a resolution of the scene, a sparse tree is placed in a texture of 2080x2080 (16.6 Mb).
Creating an array of voxels
To create a voxel array, you need to voxelize all the objects in the scene. Let's take advantage of the simple voxelization from the related Octree-Based Sparse Voxelization article . This technique is easy to implement and works in one GPU pass.

Pipeline voxelization object [SV]
Calculate the bounding box of the scene. Set the viewport to resolve the voxelized scene (for example, 256x256). We place the orthographic camera over the stage so as to fit the bounding cube. Render each scene object that we want to consider.
In the geometric shader, we handle the triangles of an object. Using the normal of the triangle, the axis is selected in the direction of which the projection area of this triangle is maximum. Depending on the axis, we rotate the triangle with the largest projection to the rasterizer - so we get more voxels.
In a pixel shader, each fragment will be a voxel. Create a Voxel structure with coordinates, color and normal, and add it to the voxel array.
At this stage, it is desirable to use low-poly LODs (LODs) of objects, so as not to have problems with missing voxels and with the merging of voxels of adjacent triangles (such cases are discussed in [SV]).



Voxelization artifacts - not all triangles are rasterized. Use low poly lodes or stretch triangles additionally.
Creating an Octree on a Voxel List
When the whole scene is voxelized, we have an array of voxels with their coordinates. From this array, you can build SVO, with which we can find voxels in space. Initially, each pixel of a texture with SVO is initialized to 0xffffffff. To write tree nodes through a shader, the SVO texture will be represented as a UAV resource (RWTexture2D). To work with the tree, we will start an atomic node counter (D3D11_BUFFER_UAV_FLAG_COUNTER).
Let us describe in stages the algorithm for creating an octree. Under the node address in SVO, we further mean the index of the node, which is converted to the 2D coordinates of the texture. Further, allocation of a node means the following set of actions:
- Using the current value of the node counter, addresses are calculated in which the child nodes of the allocated node will be located.
- The node counter is increased by the number of child nodes (8).
- Addresses of child nodes are recorded in the fields of the current node.
- In the flag field of the current node, it is recorded that it is allocated.
- The address of the current node is recorded in the parent field of the child nodes.

Schematic representation of the octree and its representation in the texture [SV]
An algorithm for creating an octree with a height N is as follows:
- We allocate the root node . Current tree level = 1. Node counter = 1.
- We sort out the voxels . For each voxel, we find a node (subspace) at the current level of the tree to which it belongs. We mark such nodes with a flag that allocation is necessary. This step can be parallelized on the vertex shader using the Input-Assembler without buffers , using only the number of voxels and the SV_VertexID attribute to address the voxel array.
- For each node of the current tree level, check the flag . If necessary, allocate the node. This stage can also be parallelized on the vertex shader.
- For each node of the current tree level, we write the addresses of neighbors in the child nodes .
- The current tree level is ++ . Repeat steps 2-5 until the current tree level is <N.
- At the last level, instead of allocating the current node, we write the voxel index in the voxel array . Thus, the nodes of the last level will contain up to 8 indices.
Having built such an octree tree, we can easily find the voxel of the scene by the coordinates in space, going down the SVO.
Creating an octree block buffer
Now that we have constructed the octree of the voxelized scene, we can use this information to preserve the illumination reflected by the voxels from the light sources. Illumination is saved in the 3D texture of the R8G8B8A8 format. This will allow us to use trilinear interpolation of the GPU when sampling the texture, and as a result we get a smoother final image. This texture is called a brick buffer, because it consists of blocks arranged according to SVO. A block is another representation of a group of voxels in space.
Groups of 2x2x2 voxels whose indices are located in the leaves of SVO are displayed on 3x3x3 voxel blocks from 3D texture:

Mapping a group of voxels into a voxel block [DP]
Groups of voxels located next to each other in the scene can be scattered in the texture (since the texture is based on SVO). Therefore, for the correct interpolation between neighboring groups of voxels, it is necessary to do additional work on averaging the values between neighboring blocks.

Averaging the boundaries of neighboring blocks
Voxels from a block are located at the corners of the initial group of voxels and between them. Thus, blocks occupy more space in space than the original voxels. But sampling inside the block will be performed along the boundaries of the original voxels. So there is a likeness of some delimiter half a pixel wide, which is not used in any way.
Blocks arranged according to SVO leaves are a display of the original voxels. Blocks located in accordance with other SVO nodes at certain levels of the octree are MIP levels of the block buffer.

Schematic representation of the octree tree, its representation in the texture and mapping of the blocks to the buffer [SV]
At the same time, the blocks do not have to be 3x3x3, they can be 2x2x2, and 5x5x5 is a matter of accuracy of the representation. 2x2x2 blocks would be another good way to save memory, but I have never seen such an approach.

Comparison of interpolation when sampling four neighboring voxels: without a block buffer, from a block buffer of 3x3x3 and from a buffer of blocks 5x5x5
Creating such a block buffer is a rather time-consuming task. We will create two buffers: for storing scene transparency and for storing lighting.
Steps for creating a block buffer
The first step is to fill in the voxels of the blocks matched with the leaves of the octree. Suppose we compute reflected light in specific SVO voxels. Then these values will be displayed in the corresponding angular voxels of the block buffer.

After the calculation of outgoing lighting is completed, for each block we add the remaining voxels with the averaged values of the neighboring voxels inside the block:

Now average the values between the neighboring blocks. That is why neighbors in space are stored in the nodes of the tree.

One of the options for averaging the block buffer is along each axis in three passes. Possible artifacts with this averaging are marked with a red rectangle [DP]
Create the MIP levels of such a buffer. The nodes of the upper levels of SVO will be displayed in blocks that contain the averaged values from the underlying level. Each block corresponding to a node from the top level of the tree includes information from blocks of the corresponding descendants. It can also be blocks that correspond not only directly to the child nodes in the tree, but also to their neighbors (see the figure below).

On the left - the block includes information from child blocks and their neighbors. Right - a block includes information only from child blocks [DP]
To reduce the number of memory accesses, only voxels of child blocks are used for each block being calculated (figure on the right). After that, the values between neighboring blocks are averaged, as described above. And so we create the MIP levels until we get to the root node of SVO.
Let's create two buffers - a buffer of scene transparency blocks and a buffer of reflected light blocks.
The buffer of transparency blocks is preliminarily created based on the voxelized geometry of the scene. We will keep directional voxel transparency. To do this, fill in the RGB values of the voxels of the blocks from the lower level in accordance with the transparency of the voxels, and when creating the MIP levels of the blocks for each calculated voxel, we will choose the average maximum transparency value along the XYZ axes, and save them in the corresponding RGB texture values. This solution helps to take into account the blocking of light in space in a certain direction.

In each direction, a maximum in the transparency value is selected (i.e. 1.0 is a completely opaque object, and this value will be maximum). Further, when constructing MIP levels, the maxima along the XYZ axes in the daughter blocks are averaged and added to the RGB components. [DP]
Reflective baking
Lighting reflected by a voxel is calculated by processing the shadow map from the calculated light sources. Using this map, we can get the coordinates of objects in space and, using SVO, transform them into indices of illuminated voxels.
Usually the resolution of the shadow map is higher than the resolution of the octree. The original article describes an approach in which each pixel in the shadow map is considered a conditional photon. Accordingly, depending on the number of photons there will be a different contribution to the illumination. In my implementation, I simplified this stage and counted the illumination only once for each voxel that fell into the shadow map.
To avoid repeated calculations, for each voxel for which the reflected lighting has already been calculated, we will use the flag bit of the octree node that stores the pointer to the voxel. Also, when processing the shadow map, among the pixels included in the same voxel, you can select only the top left one for calculation.


Fragment of the shadow map (left). On the right - the upper left pixels that are part of the same voxel are shown in red.
To calculate the reflected illumination, the standard albedo * lightColor * dot (n, l) is used, but in the general case it depends on BRDF. The calculated illumination is recorded in the buffer of the lighting units. After processing the shadow map, the block buffer is refilled and MIP levels are created, as described above.
The algorithm is quite expensive. It is necessary to recalculate the buffer of the lighting units with each change in lighting. One of the possible optimization methods is to smear a buffer update by frames .
Create G-Buffer
In order to apply voxel tracing to cones for a specific pixel, you need to know the normal and location of the pixel in space. These attributes are used to bypass SVO and sample the lighting block buffer. You can get these attributes from G-buffer .
Using G-buffer, you can also calculate the reflected light at a lower resolution than the viewport, which improves performance.
Tracing voxels with cones
When the buffer of lighting blocks is calculated, we can proceed to the calculation of lighting reflected from the scene to objects in the frame — that is, global lighting. To do this, trace voxels with cones.
For each pixel, several cones are emitted in accordance with BRDF. In the case of the Lambert lighting model, the cones are emitted uniformly in a hemisphere oriented using the normal derived from the G-buffer.

Emitting cones from the surface for which incoming lighting is calculated [VCT]
In the calculation, we assume that the illumination obtained from a point on the surface in the voxel direction will be the same as that emitted from the voxel towards the surface in a certain cone of visibility.

[VCT]
Tracing is done step by step. At each step, the buffer of the lighting blocks is sampled in accordance with the level of the octree tree (i.e., in accordance with the created MIP levels), starting from the lowest to the highest.

Sampling the block buffer using a cone in accordance with the SVO [DP] levels
Tracing with a cone is performed similarly to rendering volumetric objects [A]. Those. the alpha front-to-back model is used, in which at each next step along the cone, color and transparency are calculated as follows:
с’ = с’ + ( 1 — а’ ) * с
а’ = а’ + ( 1 — а’ ) * аwhere a is transparency, c is the value obtained from the buffer of lighting blocks multiplied by transparency (premultiplied alpha).
The transparency value is calculated using the transparency block buffer:
opacityXYZ = opacityBrickBuffer.Sample( linearSampler, brickSamplePos ).rgb;
alpha = dot( abs( normalize( coneDir ) * opacityXYZ ), 1.0f.xxx );In other words, transparency is read in the direction of the cone at a particular point. This is not the only approach. You can, for example, store transparency in the alpha channel of the lighting block buffer. But then the direction of the reflected light is lost. I also tried to store directional illumination in six buffers of lighting units (two for each axis) - there are more costs than visible advantages.
The final result for the cones is weighted summarized depending on the angles of the cones. If all the cones are the same, the weight is divided equally. The choice of the number of cones and the size of the solution angles is a question of the ratio of speed and quality. In my implementation, 5 cones of 60 degrees (one in the center, and 4 on the sides).
The figure above schematically shows the sampling points along the axis of the cone. It is recommended to choose the location of the samples so that the octree node from the corresponding level fits into the cone. Or you can replace it with the corresponding sphere [SB]. But then sharp voxel boundaries may appear, so the location of the samples is adjusted. In my implementation, I just move the samples closer to each other.
As a bonus to reflected light, we also get Ambient Occlusion shading , which is calculated based on the alpha value obtained during the trace. Also, when calculating AO at each step along the axis of the cone, a correction is made depending on the distance
1 / (1 + lambda * distance), where lambda is the calibration parameter.The result is saved in the RGBA texture (RGB for lighting and A for AO). For a smoother result, a blur can be applied to the texture. The final result will depend on the BRDF. In my case, the calculated rereflection is first multiplied by the surface albedo obtained from G-buffer, then optionally multiplied by AO, and finally added to the main lighting.
In general, after certain settings and improvements, the picture is similar to the result from the article.



Comparison of results - on the left is a scene rendered in Mental Ray, on the right is Voxel Cone Tracing from the original article, in the center is my implementation.
Underwater rocks
The problem of self-lighting . Since in most cases the surface is physically located in its own voxels, it is necessary to somehow deal with self-lighting. One solution is to push the beginning of the cones in the direction of the normals. Also, this problem can theoretically be avoided if the directional distribution of lighting is stored in voxels.
Performance issue . The algorithm is quite complex, and you will have to spend a lot of time on an effective implementation on the GPU. I wrote the implementation "head-on", using fairly obvious optimizations, and the load turned out to be high. At the same time, even an optimized algorithm when searching for voxels in a tree will require a lot of SVO texture samples depending on each other.
In my implementation, I emit 5 cones, sampling block buffers for the 4 penultimate levels of the 256x256x256 octree tree. According to the Intel GPA, the relative performance distribution is as follows:

Performance distribution. G-Buffer and Shadow Map without prior cooling.
In the original article, three diffuse cones are used on a 512x512 texture throughout SVO (512x512x512 - 9 levels). Together with direct lighting, this takes ~ 45% of the frame time of 512x512. There is much to strive for. It is also necessary to pay attention to optimizing the updating of the lighting buffer.
Another problem of the algorithm is the leakage of light through objects(light leaking). This happens with thin objects that make a small contribution to the transparency block buffer. Also, planes located next to illuminated voxels of the lower levels of SVO are affected by this phenomenon:


Light leaking: on the left when using the VCT algorithm, on the right - in real life. This effect can be mitigated with AO.
From the foregoing, another consequence follows: it is not so easy to configure the algorithm to get a good picture - how many cones to take, how many SVO levels, with what coefficients, etc.
We considered only static objects in the scene. To store dynamic objects, you will need to modify the SVO and corresponding buffers. As a rule, in this case it is proposed to separately store static and dynamic nodes.
To summarize, I would not recommend this technique if you do not have enough time, patience and strength. But then it will help to achieve a plausible ambient-lighting.
Demonstration in dynamics:
Link to the application: https://github.com/Darkxiv/VoxelConeTracing (bin / VCT.exe)
List of sources and resources that can help in the implementation of voxel tracing by cones:
- [VCT] Original article: http://research.nvidia.com/sites/default/files/publications/GIVoxels-pg2011-authors.pdf
- [SV] Addendum to the original article explaining voxelization and SVO: https://www.seas.upenn.edu/~pcozzi/OpenGLInsights/OpenGLInsights-SparseVoxelization.pdf
- [S4552] NVIDIA Presentation: http://on-demand.gputechconf.com/gtc/2014/presentations/S4552-rt-voxel-based-global-illumination-gpus.pdf
- [A] Alpha front-to-back model: http://developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch39.html
- [DP] Diploma based on the original article: http://dcgi.felk.cvut.cz/theses/2013/drinotom
- [SB] Description of another implementation of VCT: http://simonstechblog.blogspot.ru/2013/01/implementing-voxel-cone-tracing.html
- UE4 implementation slides: https://www.yumpu.com/en/document/view/4694219/the-technology-behind-the-elemental-demo-unreal-engine
- Explanation of sampling ambient cubes: http://www.valvesoftware.com/publications/2006/SIGGRAPH06_Course_ShadingInValvesSourceEngine.pdf
- NVIDIA sparse octree library https://developer.nvidia.com/gvdb
