Binary Tree Numbering
How to number all binary trees? As on KDPV: a “tree” from one leaf will be the first, a tree from two leaves the second, a second tree with another branch coming from the root - the third. And how to find the number of an arbitrary tree in such a scheme?

First of all, the scooter is not mine. The circuit described in the article was published by Caroline Colillin and Giovanni Plazotta (C. Colijn, G. Plazzotta) in Systematic Biology . But since most of the habr is unlikely to read English biological journals, I decided that it was worth a piece from there to translate.
Suppose that we already have some kind of numbering scheme, and the numbering starts with a simple tree consisting of one sheet. We call a tree consisting of two subtrees with numbers k and j such thatk > = j , (k, j) -tree . We set the set of ( k , j ) -trees lexicographically: (1), (1, 1), (2, 1), (2, 2), (3, 1), (3, 2) ... The desired number is exactly there will be a place for the tree in that order. That is, a (1, 1) -tree is the same as tree number 2, a (2, 1) -tree is the same as tree number 3, and so on. You can check: on KDPV the way it is.
To translate a ( k, j ) -notation into numbers, one should pay attention to the fact that this is essentially a sequence of all possible pairs of natural numbers. Since k > = j > = 1 by definition, there exists exactly k ( k , j) is a pair, from ( k , 1) to ( k , k ), for any k . Therefore, the ( k , 1) -pair has the number (1 + 2 + 3 + ... + k -1) + 1, because it is preceded by (1 + 2 + 3 + ... + k -1) pairs. And, of course, the number of ( k , j ) -pairs is greater than the number of ( k , 1) -pairs by ( j -1). Substituting the formula for the sum of the arithmetic progression and reducing the excess units, we arrive at the following formula:
The extra unit is explained by the fact that the sequence begins not with the (1, 1) -, but with the (1) -tree. Now the number of any arbitrary tree can be calculated in a recursive manner. The target tree is by definition a ( k , j ) -tree, where k and j are subtrees growing from its root. The k- tree, in turn, is a ( k1 , k2 ) -tree, where k1 and k2 are its subtrees, and so on up to leaves that are (1) -trees. For instance:
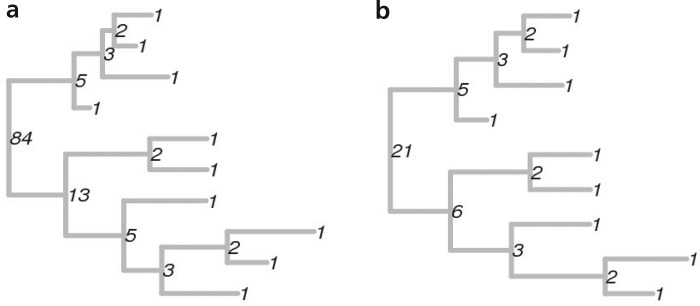
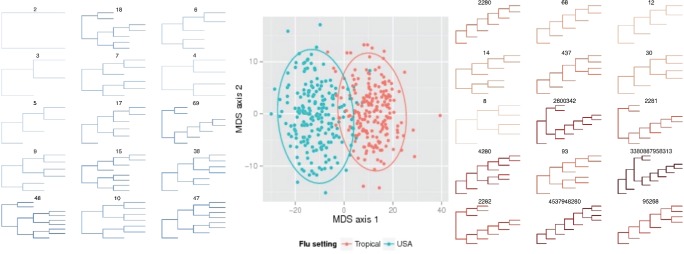
From this method of calculating the number follows the practical meaning of the whole undertaking. Actually the numbers are a cool thing, but it is not very clear what to do next. Is it possible to admire how a huge number took up your entire RAM and wants more (in practice: marking up about a dozen trees with 500 leaves does not fit in 64 GB even using gmpy2) They vary too much even with slight changes in the trees; two trees in the picture above, for example, differ only in the fact that in the right one sheet is missing at the very bottom. But each tree also has a vector of numbers of all its internal nodes. And on vectors it is already possible to define a distance metric (for example, Euclidean) and use it to cluster tree topologies. In the original article, the trees were phylogenetic and it was possible to identify differences in the evolution of the influenza virus in the United States and the tropics. In the tropics, the disease occurs year-round, therefore, all intermediate forms are observed (mass of ( k , 1) -trees on the right). But in America, influenza is a seasonal matter and is mainly brought in from abroad, so there are practically no such trees.
In the original articlethere is still a lot of interesting things: in particular, generalization for non-binary trees, various practically useful options for distance metrics, proof that these are really metrics in the strict sense, the definition of mathematical operations on trees, and so on. If you suddenly want to play, the author's code for R and my python implementation are available on the github. Both of them, however, are designed for phylogenetic trees.

First of all, the scooter is not mine. The circuit described in the article was published by Caroline Colillin and Giovanni Plazotta (C. Colijn, G. Plazzotta) in Systematic Biology . But since most of the habr is unlikely to read English biological journals, I decided that it was worth a piece from there to translate.
Suppose that we already have some kind of numbering scheme, and the numbering starts with a simple tree consisting of one sheet. We call a tree consisting of two subtrees with numbers k and j such thatk > = j , (k, j) -tree . We set the set of ( k , j ) -trees lexicographically: (1), (1, 1), (2, 1), (2, 2), (3, 1), (3, 2) ... The desired number is exactly there will be a place for the tree in that order. That is, a (1, 1) -tree is the same as tree number 2, a (2, 1) -tree is the same as tree number 3, and so on. You can check: on KDPV the way it is.
To translate a ( k, j ) -notation into numbers, one should pay attention to the fact that this is essentially a sequence of all possible pairs of natural numbers. Since k > = j > = 1 by definition, there exists exactly k ( k , j) is a pair, from ( k , 1) to ( k , k ), for any k . Therefore, the ( k , 1) -pair has the number (1 + 2 + 3 + ... + k -1) + 1, because it is preceded by (1 + 2 + 3 + ... + k -1) pairs. And, of course, the number of ( k , j ) -pairs is greater than the number of ( k , 1) -pairs by ( j -1). Substituting the formula for the sum of the arithmetic progression and reducing the excess units, we arrive at the following formula:
The extra unit is explained by the fact that the sequence begins not with the (1, 1) -, but with the (1) -tree. Now the number of any arbitrary tree can be calculated in a recursive manner. The target tree is by definition a ( k , j ) -tree, where k and j are subtrees growing from its root. The k- tree, in turn, is a ( k1 , k2 ) -tree, where k1 and k2 are its subtrees, and so on up to leaves that are (1) -trees. For instance:

From this method of calculating the number follows the practical meaning of the whole undertaking. Actually the numbers are a cool thing, but it is not very clear what to do next. Is it possible to admire how a huge number took up your entire RAM and wants more (in practice: marking up about a dozen trees with 500 leaves does not fit in 64 GB even using gmpy2) They vary too much even with slight changes in the trees; two trees in the picture above, for example, differ only in the fact that in the right one sheet is missing at the very bottom. But each tree also has a vector of numbers of all its internal nodes. And on vectors it is already possible to define a distance metric (for example, Euclidean) and use it to cluster tree topologies. In the original article, the trees were phylogenetic and it was possible to identify differences in the evolution of the influenza virus in the United States and the tropics. In the tropics, the disease occurs year-round, therefore, all intermediate forms are observed (mass of ( k , 1) -trees on the right). But in America, influenza is a seasonal matter and is mainly brought in from abroad, so there are practically no such trees.

In the original articlethere is still a lot of interesting things: in particular, generalization for non-binary trees, various practically useful options for distance metrics, proof that these are really metrics in the strict sense, the definition of mathematical operations on trees, and so on. If you suddenly want to play, the author's code for R and my python implementation are available on the github. Both of them, however, are designed for phylogenetic trees.
