Procedural worlds from simple tiles

In this post, I will describe two algorithms for creating complex procedural worlds from simple sets of color tiles and based on restrictions on the location of these tiles. I will show how with the neat design of these sets of tiles you can create interesting procedurally generated content, for example, landscapes with cities or dungeons with a complex internal structure. The video below shows a system that creates a procedural world based on rules encoded in 43 color tiles.


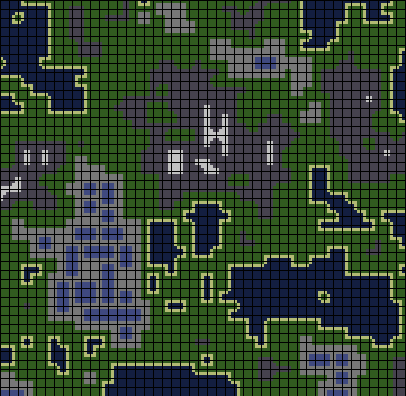
The image below shows a set of tiles (tileset), based on which the world from the video is generated. The world is equipped with notes to help present it in a real environment.


We can define tiling as a finite grid in which each of the tiles is in its own grid cell. We define the correct world as a world in which the colors along the edges of neighboring tiles must be the same.


Tiling has only one iron rule: the colors of the edges of tiles must match. The entire high-level structure is developed based on this rule.

The correct tiling looks like this:


This is tiling, which should represent a map with water, coasts, grass, cities with buildings (blue rectangles), and mountains with snowy peaks. The black lines show the boundaries between the tiles.

I think this is an interesting way to describe and create worlds, because very often in the algorithms of procedural generation the “top-down” approach is used. For example, in L-systems, a recursive description of the object is used, in which high-level, large parts are determined earlier than low-level ones. There is nothing wrong with this approach, but I think it’s interesting to create sets of tiles that can only encode simple low-level relationships (for example, sea water and grass should be separated by the coast, buildings should only have convex angles at 90 degrees angles) and observe behind the emergence of higher-level patterns (e.g. square buildings).

Tiling is an NP-Complete Problem of Satisfying Constraints

For a reader who is familiar with constraint satisfaction problems (CSP), it is already obvious that tiling of the final world is a CTA. In the ZUO, we have many variables, many values ​​that each variable (called the domain of its definition) can take, and many restrictions. In our case, the variables are the coordinates on the map, the scope of each variable is a tileset, and the restrictions are that the edges of the tiles must correspond to the edges of the neighbors.

It is intuitively clear that the task of correctly creating non-trivial tiling is complex, since tilesets can encode arbitrary extensive dependencies. When we consider a tileset as a whole, from a formal point of view this is an NP-complete task of satisfying restrictions. The naive algorithm for creating tiling is an exhaustive search for the tiling space and is performed in exponential time. There is a hope that we can create interesting worlds on the basis of tilesets solved by a search that can be accelerated by heuristics. Another option is to create tilings that are approximately true, but contain a small number of incorrect locations. I found two algorithms that work well with some interesting tilesets, and I will describe them below.

Method 1: greedy with reverse transitions

We select random places and put appropriate tiles there. If we get stuck, delete some of them and try again.

Инициализируем всю карту как НЕРЕШЁННУЮ

пока на карте остаются НЕРЕШЁННЫЕ тайлы
если на карте можно разместить любой подходящий тайл
t <- коллекция всех возможных расположений подходящих тайлов
l <- случайная выборка из t, взвешенная по вероятностям тайлов
располагаем l на карте
иначе
выбираем случайный НЕРЕШЁННЫЙ тайл и присваиваем всем его соседям состояние НЕРЕШЁННЫЙ


The first attempt to create tiling from the tileset was that the entire grid was in an unresolved state, after which I iteratively placed a random tile in a suitable place for it, or, if there were no suitable places, assigned a “unresolved” state to a small area next to the unresolved tile. and continued the greedy location of the tiles. “Greedy location” is a strategy for arranging a tile until its edges correspond to already placed tiles, regardless of whether this arrangement creates a partial tiling that cannot be completed without replacing the already set tiles. When such a situation arises and we can no longer arrange tiles, we must delete some of the previously located tiles. But we don’t know which of them is best removed, because if we could solve the problem, then, probably, could also first of all solve the problem of the correct arrangement of tiles. To give the algorithm one more chance to find a suitable tile for a given area, we assign all the tiles around the unresolved point an “unresolved” state and continue to execute the greedy strategy. We hope that sooner or later the correct tiling will be found, but there are no guarantees. The algorithm will be executed until the correct tiling is found, which can take infinite time. He does not have the ability to determine that a tileset is unsolvable. We hope that sooner or later the correct tiling will be found, but there are no guarantees. The algorithm will be executed until the correct tiling is found, which can take infinite time. He does not have the ability to determine that a tileset is unsolvable. We hope that sooner or later the correct tiling will be found, but there are no guarantees. The algorithm will be executed until the correct tiling is found, which can take infinite time. He does not have the ability to determine that a tileset is unsolvable.

There are no guarantees that the algorithm will complete its work. A simple tileset with two tiles that do not have common colors will force the algorithm to execute an infinite loop. An even simpler case would be a single tile with different colors on top and bottom. It would be wise to find some way to determine if tilesets cannot create the correct tiling. We can say that a tileset is definitely true if it can bridge an infinite plane. In some cases, you can easily prove that a tileset may or may not bridge an infinite plane, but in the general case this problem is unsolvable. Therefore, the task of the designer is to create a tileset capable of creating the correct tiling.

This algorithm is unable to find good solutions for the dungeon tileset from the video at the beginning of the post. It works well with simpler tilesets. We would like to learn how to solve more complex tilesets with many possible types of transitions between tiles and various coded rules (for example, that roads should start and end near buildings).

We need an algorithm that can look ahead and create tile locations, somehow aware of the options at which these locations are open for future tile locations. This will allow us to efficiently solve complex tilesets.

In terms of meeting restrictions

This algorithm is similar to reverse lookup. At each step, we try to assign one variable. If we cannot, then we unassign the variable and all the variables that are attached to it by constraints. This is called “backjumping” and differs from backtracking, in which we unassign one variable at a time until we can continue to make the correct assignments. When returning, we generally cancel the assignment of variables in the reverse order with respect to their assignment, however, when reversing, we cancel the assignment of variables according to the structure of the problem under consideration. It is logical that if we cannot place any tile at a specific point, then we must change the location of neighboring tiles, since their location created an unsolvable situation.

No local integrity methods are used in this search. That is, we do not attempt to arrange tiles that later lead to an unsolvable situation, even through one search step in the future. Acceleration of the search is possible due to tracking the influence that the location will have on possible locations in several tiles from the current point. At the same time, it can be hoped that this will allow the search not to spend so much time canceling its work. This is exactly what our algorithm does.

Method 2: location with the greatest restrictions and the dissemination of local information

We preserve the probability distribution for tiles at each point, making non-local changes to these distributions when deciding on the location. We never go back.


Next, I will describe an algorithm that is guaranteed to complete and creates more visually pleasing results for all the tiles I tested. In addition, it can create near-correct tiles for much more complex tilesets. The trade-off here is that this algorithm does not guarantee that the output will always be the correct tiling. The section “Optimizations” describes optimizations that allow you to execute this algorithm faster even with larger tilesets and maps.

The complexity of creating the correct tiling strongly depends on the number of transitions required to transition between the two types of tiles. A simple tileset can only have sand, water and grass. If grass and water cannot touch each other, then between them there must be a transition to the sand. This is a simple example that can easily solve the previously presented algorithm. In a more complex case, multiple built-in levels of tile types may be represented. For example, we can have deep water, water, sand, grass, a high plain, a mountain, and a snowy peak. In order for all these types of tiles to appear on the map, seven transitions are necessary if we assume that these types cannot touch each other except in the order I specified. Additional complexity can be added by creating tiles,

Intuitively, the algorithm for this task should be able to “look ahead” and consider at least a few transitions that may be the consequences of the selected location. To realize this, you can consider a tile map as a probability distribution for tiles at each point. When an algorithm arranges a tile, it updates the probability distributions around this tile in response to its location so that the probabilities of neighboring tiles are increased, which can probably be compatible with the current location.

For example, if there is a water tile on the map, then the tiles next to it should contain water. The tiles next to them may also contain water, but there are other probabilities, for example, grass, if the coast is placed next to the original water tile. The farther we go from the located tile, the more types of tiles it becomes possible. To take advantage of this observation, we can count the number of ways we can get to the location of each tile next to the original tile. In some cases, only a single sequence of transitions can lead to the transition of one tile to another at a given distance. In other cases, there may be many different transition sequences. After the location of the tile, we can determine the probability distributions of the tiles at neighboring points, counting the number of ways, with which we can make the transition from the tile that we located to the neighboring tiles. The “look forward” performed by this algorithm is tracking such numbers of transitions and processing them as probability distributions from which you can select new tiles that are available.


At each step, the algorithm examines all the unresolved locations of the tiles, each of which has a probability distribution over the tiles, and selects one location for converging to the tile. He selects a distribution from a map with minimal entropy. For multinomial distributions with low entropy, the probabilities are usually concentrated in several modes, so the convergence of the first ones leads to the effect of arranging tiles for which some of the limitations already exist. That is why the algorithm places the tiles next to the tiles that we decided first.

This is the most efficient algorithm that I managed to implement for this task. It has one more advantage: it creates beautiful visualizations when executed. Perhaps there is a way to improve this algorithm by introducing some form of backtracking. If the wrong ready tiling exists in the resulting ready tiling, then canceling the locations of neighboring tiles and resampling from the resulting distributions at their points may allow us to find a fix for this ready tiling. Of course, if you want to continue the search until you find the correct tiling, then exceed the limits of the specified guaranteed runtime.

Optimizations

The most important operation of this method is updating probabilities around the located tile. One approach would be to count possible transitions “out” from the located tile each time the tile is located. This will be very slow, because for each point on the map to which new probabilities will apply, it will be necessary to consider many transition pairs. An obvious optimization would be to perform a distribution not to the entire map. A more interesting optimization is to cache the effect that each tile location on the points around it will have, so that each tile location will simply search to check what types of changes the location brings to neighboring probabilities, and then apply this change using some simple operations. Below I will describe my implementation of this optimization method.

Imagine a tile placed on a completely empty card. This location will update the probabilities of neighboring tiles. We can consider these updated distributions as having a previous distribution defined by previous tile locations. If multiple tiles are placed, then this previous distribution will be shared. I approximate this posterior probability with the previous joint as a product of distributions for each location in the past.


To realize this, I will imagine that when a tile is placed on an empty map, it makes significant changes to the distribution of neighboring map points. I will call these updates the scopetile, that is, the sphere of influence of the tile projected around it when placing it on an empty card. When two tiles are located next to each other, their spheres interact and create finite distributions that are affected by both locations. Given that many tiles can be located next to a given unresolved location, there will be a large number of interacting restrictions, making a decision based on the calculation to determine the probability of the appearance of different tiles at this point in a very slow process. What if, instead, we consider only a simple model of the interaction between pre-computed areas of tiles that were already located on the map?


When placing the tile, I update the probability map for each element, multiplying the distribution of the sphere of this tile by each point on the map by the distribution already stored at this point on the map. It may be useful to consider an example of what this can do with a distribution map. Suppose a given map point currently has a distribution that is equally likely to select grass or water, and we place a water tile next to that point. A water tile sphere will have a high probability of water next to a water tile and a low probability of a grass tile. When we multiply these distributions element by element, the probability of water as a result will be high because it is a product of two high probabilities, but the probability of grass will become low because it is a product of high probability stored on a map with a low probability,


This strategy allows us to effectively approximate the effect that each tile location on the probability map should have.

In terms of satisfying restrictions

To effectively solve constraint satisfaction problems, it is often wise to track those assignments of other variables that become impossible when assigning a particular variable. This principle is called the introduction of local compatibility conditions. The introduction of some kind of local compatibility allows you to avoid assigning a variable a value when assigning an adjacent variable an incompatible value when you need to go back. Such transformations are referred to in the field of methods of propagation of constraints in the ZO literature. In our algorithm, we distribute information to a small area of ​​the map each time we place a tile. The disseminated information tells which tiles can and which cannot occur nearby. For example, if we have a mountain tile, we know that in two tiles from it there cannot be an open sea tile, that is, the probability of a sea tile at all points of the map in two tiles from a located tile is zero. This information is recorded in the areas of which we spoke above. Spheres encode the local compatibility that we want to impose.

By reducing the number of possible assignments of neighboring tiles, we significantly reduce the search space that the algorithm should process after each location. We know that in this small neighborhood all the probabilities of the appearance of incompatible tiles are zero. This is similar to removing these values ​​from the variable definition areas at these points. That is, each pair of neighboring points of the area around the located tile has in its definition area a certain tile that is compatible with some tile that is still in the definition area of ​​neighbors. When two variables are connected by a constraint in the MA problem, and their domains of definition contain only values ​​that satisfy the constraint, then they are said to have arc compatibility, that is, this method is actually an effective strategy for introducing arc compatibility.

In the ZUO, the “most limited” variable in the given partial assignment is the one with the least possible values ​​left in the definition area. The principle of placing a tile at a point with a minimum distribution of entropy on the map is similar to assigning the value of the most restricted variable in the ZUO, which is the standard heuristic for arranging variables when solving the ZUO using a search.

Manipulations with tiling by changing the probabilities of choosing tiles

So far I have only talked about how to create the right tiling, but besides the correctness, other properties may be required from tiling. For example, we may need a certain ratio of the number of one type of tiles to another, or we want to guarantee that not all tiles are of the same type, even if such tiling is correct. To solve this problem, both algorithms described by me receive the basic probability associated with each tile as input. The higher this probability, the more likely this tile will be present in the finished tiling. Both algorithms make a random selection from the collections of tiles, and I will simply add weights to this random selection according to the basic probabilities of the tiles.

An example of using this principle is shown below. By changing the probability of a continuous water tile appearing, I can adjust the size and frequency of the appearance of water bodies on the map.

Create your own tilesets

In short:

• clone my repository on github
• install Processing
• in the data / repository folder change tiles.png
• use processing to open wangTiles.pde and click on the play button

Using the code posted on github (you can change it, but do it at your own peril and risk - I wrote most of it in high school), you can create your own tilesets using the image editor and watch how the tiling solver creates worlds using them . Just clone the repository and edit the dungeon.png image, and then use Processing to launch wangTiles.pde and view the animation of the generated map. Below I will describe the “language” that this tiling solver needs.

Tileset Specification

Tiles are arranged in a grid of 4x4 cells. Each cell in the upper left 3x3 area contains a color tile, and the remaining 7 pixels contain the tile metadata. The pixel under the center of the tile can be colored red to comment out the tile and exclude it from the tile set. Solvers will never put it on the card. The upper pixel in the right part of the tile can be painted black to add all four rotations of the tile to the tileset. This is a handy feature if you want to add something like an angle that exists in four orientations. Finally, the most important part of the markup is the pixel in the lower left of the tile. It controls the basic probability of a tile appearing on the map. The darker the pixel, the more likely the tile appears.

Related work

Many people have explored Wang Tiles , which are tile faces with colored faces and must match faces with tiles next to which they are placed, just like the tiles we are considering.

The Most Constrained Placement with Fuzzy Arc Consistency solver is similar to the Twitter @ExUtumno Wave Function Collapse project. This algorithm stores a map of “partially observable” assignments and takes samples from them to create the final image, which is similar to the distributions I save for tiles. These approaches differ in some aspects. For each map point, this algorithm stores binary potentials, not multinomial distributions. In addition, he does not use cached “spheres” of the number of transitions necessary to speed up the calculations, which I talked about in the “Optimization” section.

Conclusions and Acknowledgments

The application of local rules to create a high-level structure, for example, the introduction of the rule “roads have no dead ends” leads to the implementation of a system in which roads must lead from some point that is not a road to another. This is an interesting look at the task of procedural generation. This way you can encode a surprisingly wide range of interesting rules. The quality of the resulting tiling very much depends on the solver, so the improvement of the algorithms for creating tiling will be a fruitful direction for further work. So far, to solve this problem, I have not studied genetic algorithms, simulated annealing, or general algorithms for satisfying constraints. In any of these areas, it is possible to create a tileset solver that can handle a wide range of tilesets with minimal parameter settings.

I would like to thank Cannon Lewis and Ronnie McLaren for useful discussions during the work on this project. Ronnie came up with a lot of interesting ideas about the possibility of coding interesting behavior in tiles. The wave convergence algorithm arose as a result of communication with Cannon, and his advice was an important step in creating the effective approximation algorithm described in the article.