March 7, 2018 at 10:42

Mosaic in the bathroom and Diophantine equations

    It was in the evening, before going to bed. I brushed my teeth and looked tiredly at the mosaic in the bathroom. For some reason, I was interested in such a simple fact: if a rectangle of 2 × 3 cells is surrounded by cells on both sides, the area of ​​the stroke will be the same as the area of ​​the rectangle:




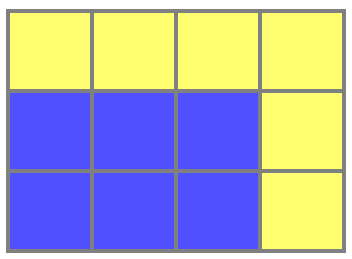
    There are exactly as many blue squares as yellow ones. And then I suffered.

    I wondered if there are still such configurations. That is, to make the rectangle$ a \ times b $circle with a contour on both sides, and the area of ​​the contour coincides with the area of ​​the rectangle. Of course$ a $ and $ b $ must be integer:



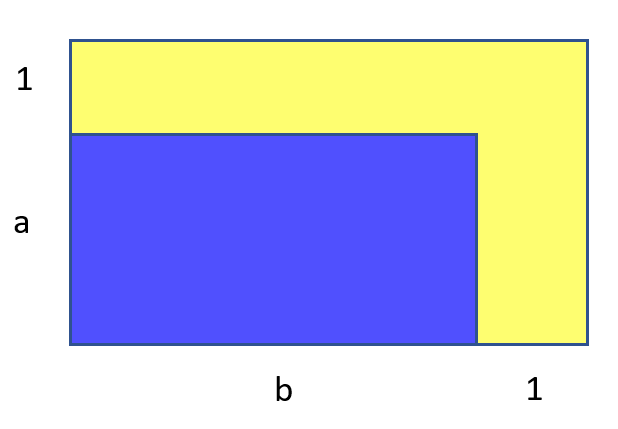
    It seems that such cases should no longer be. The area of ​​the blue part$ a \ times b $and yellow $ a + b + 1 $. It can be seen that if$ a $ or $ b $ unit, then there will be no matches, and if you increase them more $ 2 \ times 3 $then the blue will clearly grow faster. So this configuration is one.


    Bored, said the brain. We must weaken the task. So to speak:



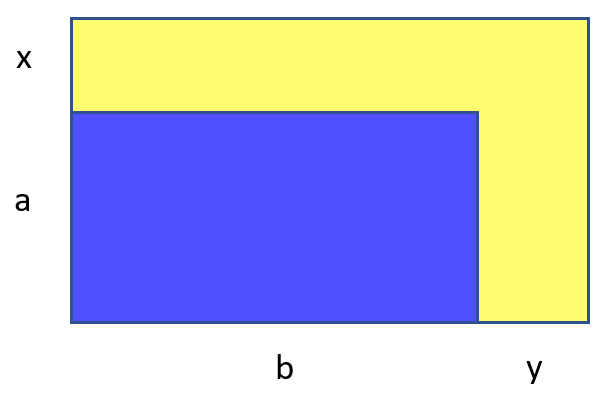
    But now the task is too weak. In fact, you need to select two rectangles with integer sides, so that their areas differ exactly by half. And the restriction on rectangles is only that one can be thrust into the other. There are too many of them, too boring. Let's do this:



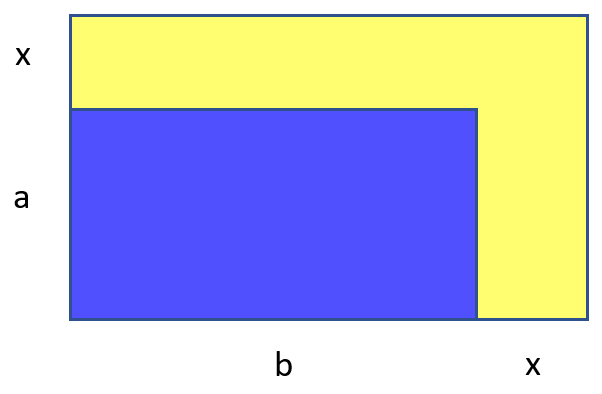
    Fix the border width. How many are there? Hm. It looks more interesting. Yellow Square is$ (x + a) (x + b) - ab $, and we want her to equal just $ ab $. That is, we (me and my brain, which dragged me into this) need to solve the equation:


    $ (x + a) (x + b) - ab = ab $


    Or, the same thing:


    $ x ^ 2 + ax + bx - ab = 0 $


    By this time, I had finished with my teeth and started pouring powder into the dishwasher. Yeah, the brain said, not a bad challenge. It is necessary to solve, of course, in integers, that is, this is a Diophantine equation . We did not go through the Diophantine equations at the university, but I remembered something about them from popular articles. Namely:


    • If we have a homogeneous equation, then we are lucky.
    • It is easy to turn a homogeneous equation on integers into an equation on rational ones, reducing the number of variables by one.
    • If, using the method of peering, to find some root of the quadratic equation on rational numbers, then it is easy to find all the others.
    • Any straight line with rational coefficients passing through a known root will go through another root. Twisting this line, you can get all the rational roots.

    In this way, for example, the general formula for all the Pythagorean triples is easily found . By the way, as with the Pythagorean triples, in our problem any number of multiple solutions. For example, a rectangle$ 4 \ times 6 $can be expanded with a border in two small squares and so on. Of course, we are only interested in multiple solutions.


    Will I be able to do all this in my mind, I thought, picking up a moisturizer. An algebra without a piece of paper and a computer is a rather insidious thing: mixed up a plus with a minus or forgot some member, and further calculations are in vain. Programmers know what to do to reduce the likelihood of an error - they need to be surrounded by unit tests. Fortunately, we already know one solution:$ x = 1; a = 2; b = 3 $. We will check it at every step.


    $ 1 ^ 2 + 2 \ times 1 + 3 \ times 1 - 2 \ times 3 = 0 $


    So far, so good. So, we have a homogeneous equation - all terms are included in the second degree. Divide the equation by$ x ^ 2 $ (happening $ x = 0 $ we are not interested, so you can share):


    $ 1 + \ frac ax + \ frac bx - \ frac ax \ times \ frac bx = 0 $


    Making a replacement: $ p = a / x; q = b / x $ and we get an equation with two rational variables:


    $ 1 + p + q - pq = 0 $


    In our unit test $ p = 2; q = 3 $, the test passes. Now we need to draw a straight line. In principle, it can be drawn just through the point$ (2; 3) $but it’s hard to keep in the brain. But by the method of peering, we can easily find another point that satisfies the equation:$ p = -1; q = 0 $. This corresponds to zero area$ a \ times b $and again, as a solution, it’s not very interesting, but for a direct one just right. It’s quite simple to notice that all the lines (except one) passing through$ p = -1; q = 0 $are described by an explicit equation $ q = \ alpha (p + 1) $(yes, for some reason the brain gave out the Greek letter, although the Latin ones did not end yet). One missing line is$ p = -1 $She is also not very interesting to us. Of course, any rational point$ (p; q) $where $ p \ neq -1 $ consistent rational $ \ alpha $. For example, for a point$ (2; 3) $ value $ \ alpha = 1 $. We substitute the equation of the line into our equation and get:


    $ 1 + p + \ alpha (p + 1) - \ alpha p (p + 1) = 0 $


    Or


    $ 1 + p + \ alpha p + \ alpha - \ alpha p ^ 2 - \ alpha p = 0 $


    Or


    $ 1 + p + \ alpha - \ alpha p ^ 2 = 0 $


    Or


    $ \ alpha p ^ 2 - p - (1 + \ alpha) = 0 $


    It becomes difficult to bring members in the head; the brain desperately asks for a piece of paper. But I lull the baby in my arms, there’s no time for a piece of paper. Run the unit test ($ p = 2; \ alpha = 1 $):


    $ 1 \ times 2 ^ 2 - 2 - (1 + 1) = 0 $


    Fuf, so far so good. Now we have a quadratic equation for$ p $which should actually give a rational root for any rational $ \ alpha $. How can this be, there is discriminant and all that? Okay, let's try:


    $ D = b ^ 2 - 4 ac = 1 ^ 2 + 4 \ alpha (1 + \ alpha) = 1 + 4 \ alpha + 4 \ alpha ^ 2 = (1 + 2 \ alpha) ^ 2 $


    Oh, oh, well, a full square came out. Endorphin went to the brain. He, a freak addict, seems to have sought this. Here it is the magic of mathematics: a rational number should have come out and it came out. Recall the formulas for the roots:


    $ p_ {1,2} = \ frac {-b \ pm \ sqrt D} {2 a} $


    Or in our notation:


    $ p_1 = \ frac {1 - (1 + 2 \ alpha)} {2 \ alpha} = -1 $


    $ p_2 = \ frac {1 + (1 + 2 \ alpha)} {2 \ alpha} = \ frac {1 + \ alpha} \ alpha $


    $ p_1 $ Is our reference point $ -1 $It’s not interesting for us. Our solution is$ p_2 $. Substituting it in$ q = \ alpha (p + 1) $ we get the answer:


    $p = \frac{1 + \alpha} \alpha; q = 1 + 2 \alpha$


    That is, you just need to sort out all the rational fractions as $\alpha$, и для них мы получим все рациональные решения уравнения $1 + p + q - pq = 0$ (ну кроме некоторых, которые нам не очень интересны).


    Разумеется, перебирать проще целые числа, а не рациональные. Спаивая младенцу препарат симетикона, я подставляю $\alpha = m/n$ и получаю:


    $p = \frac{1 + \frac m n} {\frac m n} = \frac {n + m} m$


    $q = 2 + \frac m n = \frac {n + 2m} n$


    (Боже, мозг, зачем ты выбрал именно $m$ и $n$? Они так легко путаются в голове! Букв мало что ли?) В нашем юнит-тесте, если $\alpha = 1$, то подойдут $m = n = 1$ и легко убедиться, что тест проходит.


    Как нам вернуться к целым числам? Вспоминаем, что мы заменили $p = a / x; q = b / x$. Значит, надо принять за $x$ любое число, кратное общему знаменателю из формул выше. В частности, подходит просто $mn$. В итоге имеем:


    $x = mn; a = mn + n^2; b = mn + 2m^2$


    Видно, что если $m$ и $n$ не взаимно простые, то и решение будет кратно их общему делителю, поэтому нам интересны только взаимно простые $m$ и $n$. Кратное решение также получится, если $n$ окажется чётным. В самом деле пусть $n = 2n'$. Тогда


    $x = 2mn'; a = 2mn' + 4n'^2; b = 2mn' + 2m^2$


    Если поделить всё на два, то получим


    $x = mn'; a = mn' + 2n'^2; b = mn' + m^2$


    Это решение симметрично первому, что вполне логично: ведь задача симметрична относительно $a$ и $b$. Таким образом, нам интересны взаимно простые $m$ и $n$, причём $n$ нечётно.


    Удобно, что выражение для $x$ получилось таким простым. Значит, у нас есть простой способ найти все некратные решения для заданной наперёд ширины окантовки $x$: это такие прямоугольники $a = x + n^2; b = x + 2(x/n)^2$, где $n$ любой нечётный делитель $x$, взаимно простой с $x/n$. Следующий прямоугольник будет для $x = 2; n = 1; m = 2; a = 3; b = 10$:



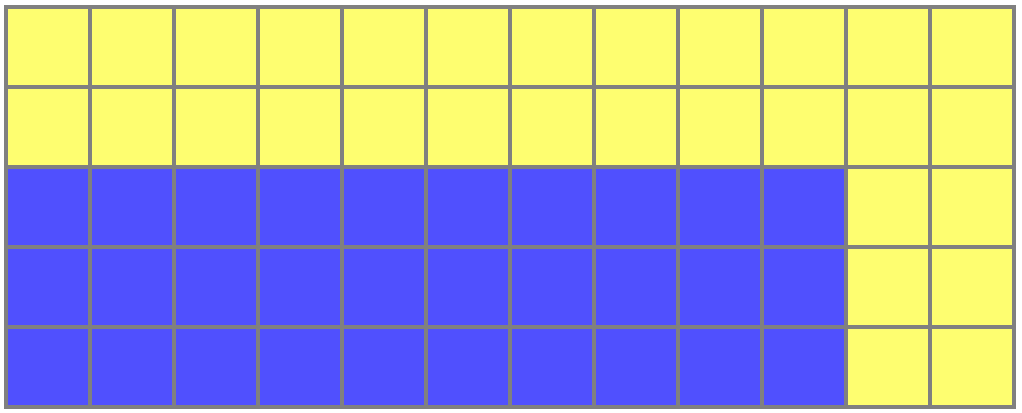
    И голубая, и жёлтая часть содержат ровно по 30 клеточек!


    Давайте посмотрим, какие ещё есть решения для маленьких $x$ ($a$ и $b$ я кое-где переставил, чтобы шли по возрастанию):


    xnmплощадь без окантовкиплощадь с окантовкой
    1112 × 3 = 63 × 4 = 12
    2123 × 10 = 305 × 12 = 60
    3134 × 21 = 847 × 24 = 168
    3315 × 12 = 608 × 15 = 120
    4145 × 36 = 1809 × 40 = 360
    5156 × 55 = 33011 × 60 = 660
    5517 × 30 = 21012 × 35 = 420
    6167 × 78 = 54613 × 84 = 1092
    63214 × 15 = 21020 × 21 = 420

    By counting these works in the head, the brain again achieved a dose of endorphin. How beautiful and wonderful divisors flow from one number to another! Take for example$6 \times 55$: the first is divided by 6, and the second is 11. We add a five to both numbers, and a miracle - now the first is divided by 11, and the second - by 6. And there are such tricks in each line! And here, and the son seemed to calm down. Eleven in the evening, you can go to bed.


    Perhaps all this can be counted easier. Perhaps my reasoning was somewhere inaccurate. Perhaps these numbers and works have some special name. I do not know - did not look. I’m more interested in this: I’m the only nonsense to occupy my consciousness, or you toosufferare you enjoying Will they treat us?

    Tags:

    Also popular now: