Methods of application and distortion of accuracy in games. Visual graphs for comparison
It is possible to calculate the fact of hitting in games on the basis of the obtained accuracy in different ways:
Accuracy bonuses can also be implemented in different ways, thereby causing players irritation for various reasons.
Similarly, the damage done can be calculated in different ways, especially on the basis of dices (cubes).
All these different approaches affect the gameplay: its complexity and predictability. Each of them can be a good solution depending on the goals pursued, therefore it is most advantageous to make a choice consciously.
The article will present visual graphs of changes in real probabilities in different approaches, which will allow them to quickly navigate and make the best decision.
Usually, when a player is informed that a character’s accuracy is 60%, he perceives this information as: “I can count on 6 hits out of 10 shots”. And if out of 10 hits he will observe 1 hit instead of 6, then he will almost certainly consider that the accident in the game is broken. He will be especially sure of this if this happens on a segment of 100 shots. In order to avoid such troubles, developers often covertly manipulate with a real probability of hitting ( or refuse from the element of randomness altogether ).
For example, in the game Fire Emblem: The Binding Blade, to determine hit with accuracy, not one random number was compared, but the average of two random numbers [ 2 ].
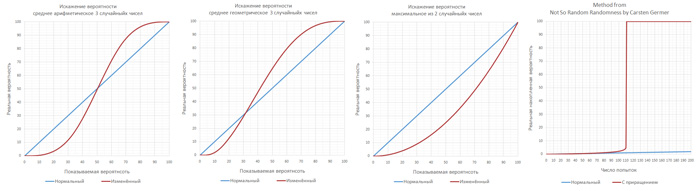
The result of this manipulation is that well-aimed attacks (> 50%) are hit much more often than they are supposed to be if they are evenly distributed, and non-targeted attacks (<50%) are hit much less often. This is how this probability distribution changes:
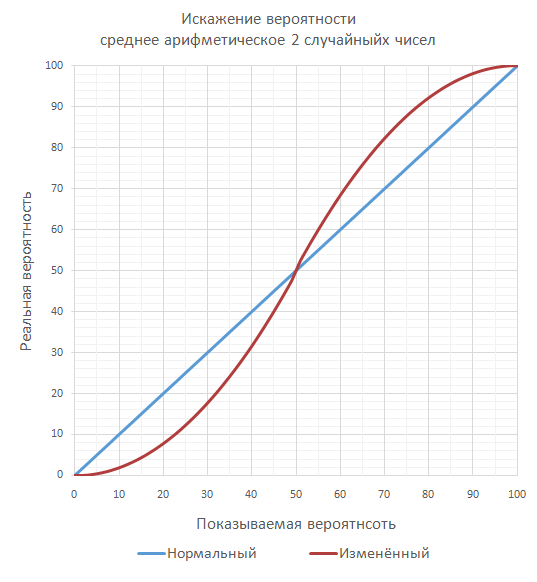
For example, with 10% accuracy shown, the actual is 1.9%. And at 75%, the actual will be 87.24%.
But, for that matter, the accuracy can be changed in many other ways.
For example, you can take an average of 3 random numbers:
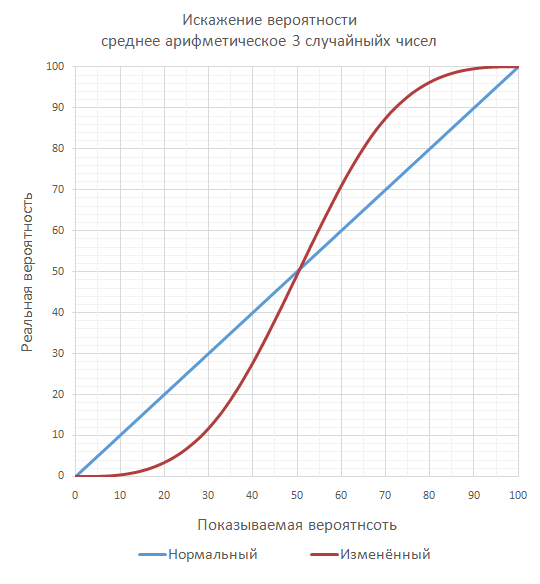
The distortion resulting from this becomes even more striking: accuracy of 10% becomes 0.41%; accuracy of 75% becomes 92.69%.
However, the average can be calculated as the geometric average. Here are the changes with an average geometric of 2 random numbers:
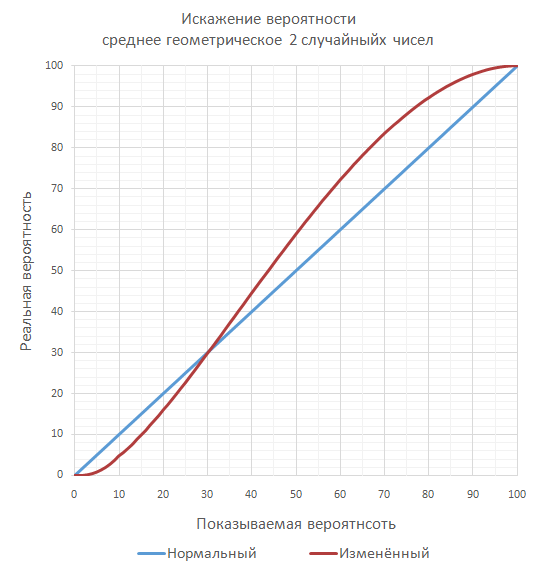
Here 10% is converted to 4.83%, and 75% to 88.18%. But, most interestingly, the transition occurs at 30%, and not at 50%, as the arithmetic average. Therefore, if you really want to be sure that the player will always have an advantage, it is enough to make sure that his minimum accuracy will never be lower than 30%, and for enemies it will be so low quite often ( for enemies you can use the arithmetic average or something more distorted ).
The geometric mean of 3 numbers leads to approximately the same results, but only with a large scatter:

Here 10% is converted to 1.95%, and 75% to 93.98%.
Often, to enhance or weaken some skills, a simpler manipulation is introduced, when one of the two or two of the random numbers is chosen as the smallest:
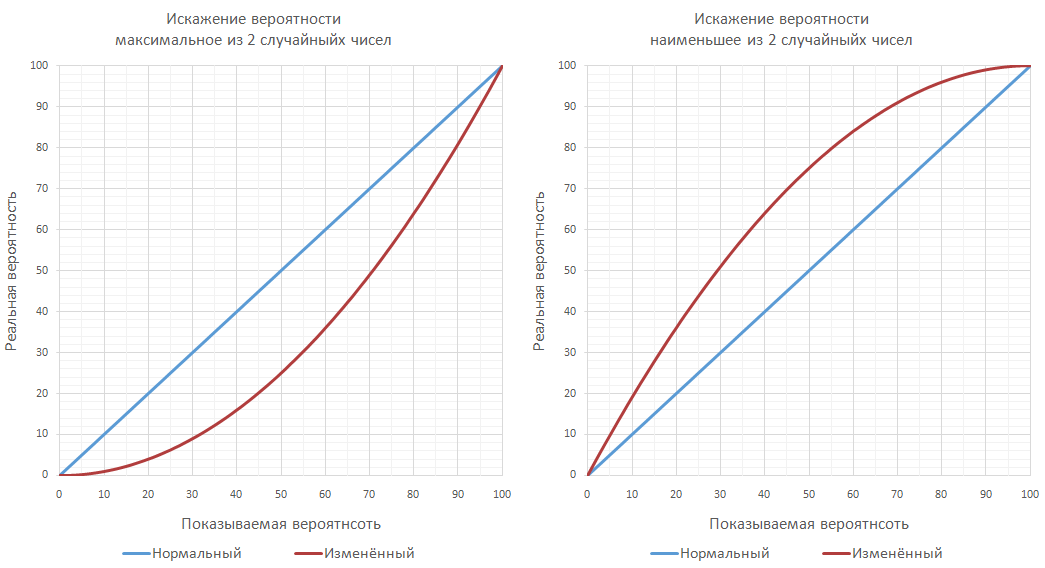
As a result, the probability of hitting changes very much. For example, if you select the smallest number, 10% accuracy is converted to 19.02%, and 75% accuracy to 93.75%.
This method, for example, is used in the game “Neverwinter Nights” in the skill “Slippery Mind”, in which in case of failure of the salvage check, a repeated check for willpower is performed [ 3 ].
 Neverwinter Nights - Pixie Warrior [ 4 ]
Neverwinter Nights - Pixie Warrior [ 4 ]
In the last article about manipulations with probabilities, a method was shown for very rare events where the probability of an event increased over time:
This is how the probability of this rare event changes when using this method:
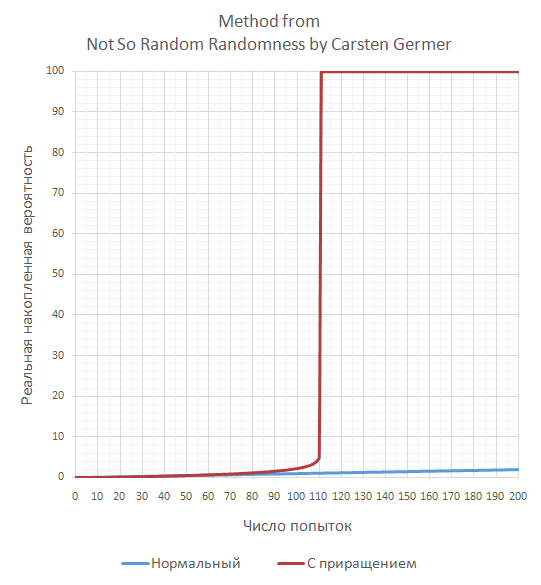
As you can see, in the end, nothing in common with the probability of 1 to 10,000, but for the purposes of gameplay, this may have been enough. Although it looks more like an unintentional concealment of real probabilities from the developer himself, which can lead to wrong decisions in future program modifications.
Below I also give a change in 1% of the event that it will occur at least once as the number of attempts grows. Distortion algorithm: the first 10 attempts - a guaranteed miss. Then, with each slip, the probability increases by 1% (0.1% and 0.01%) before it hits. Then everything is from the beginning.
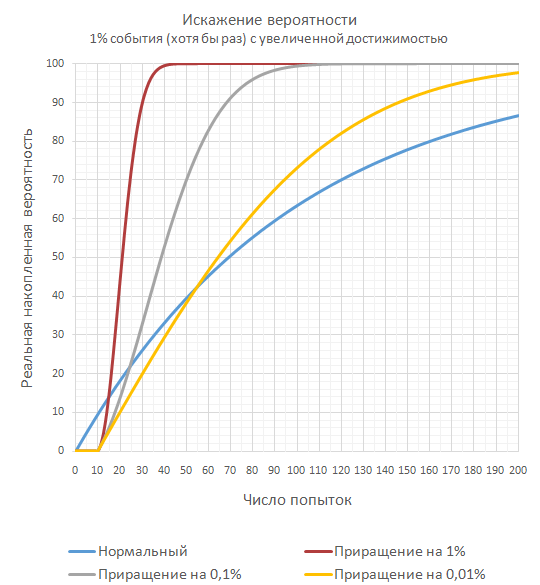
However, if your main goal, as a developer, is to ensure that a user in a 1% event does not hit a series of 1000 misses in a row, then it will be easier and more transparent after 200 misses in a row to expose a 100% hit. This will relieve you of the rare perplexities of the players and allow you to leave the program code more concise and friendlier for future improvements.
If there are few bonuses to accuracy in the game and they are easily controlled by the developer, then the easiest way is to use the simplest approach with a linear increase in accuracy by simple addition with the base value . This method is the easiest to introduce into the game and is always understandable to players. With this approach, it is possible to achieve 100% accuracy, which is not always consistent with the plans of the developer.
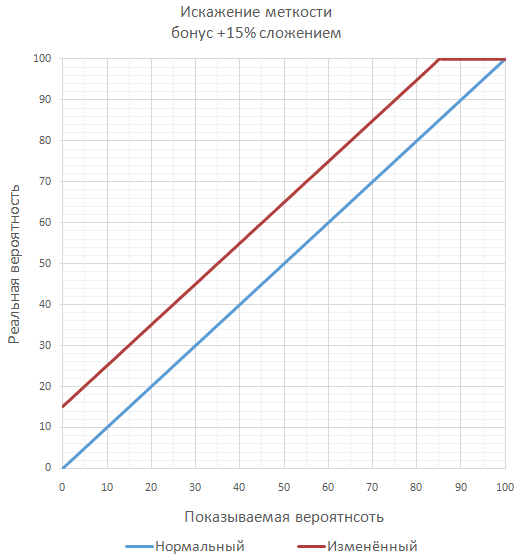
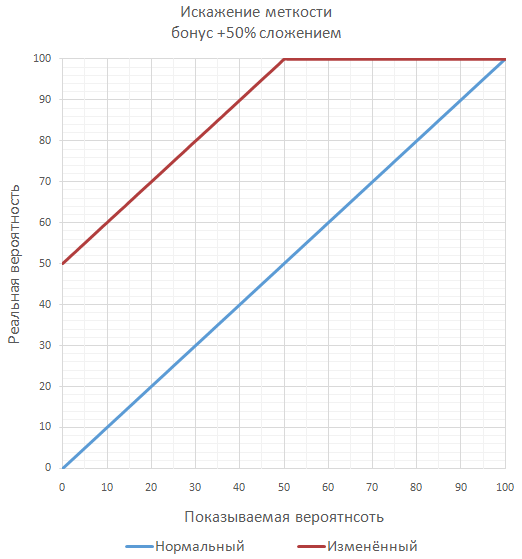
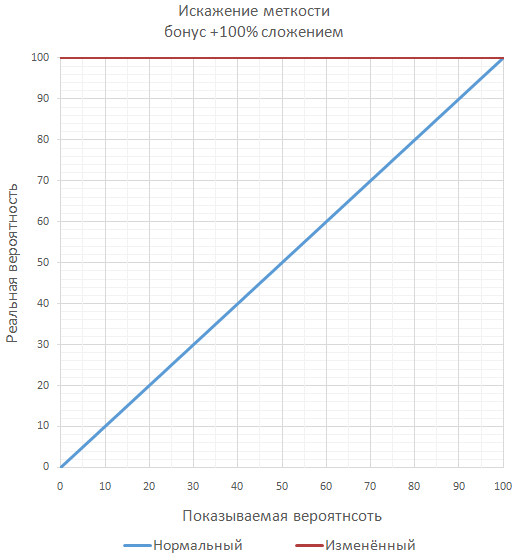
If the game is planned to have a lot of significant bonuses to accuracy, in order not to get over the guaranteed 100% accuracy, you can calculate the final accuracy as a series of additional throws ( most often unlikely separately ). For example, with a hit of 70% and a bonus of 50%, the final hit chance will be 85%, like checking two consecutive shots when at least one hit is enough.
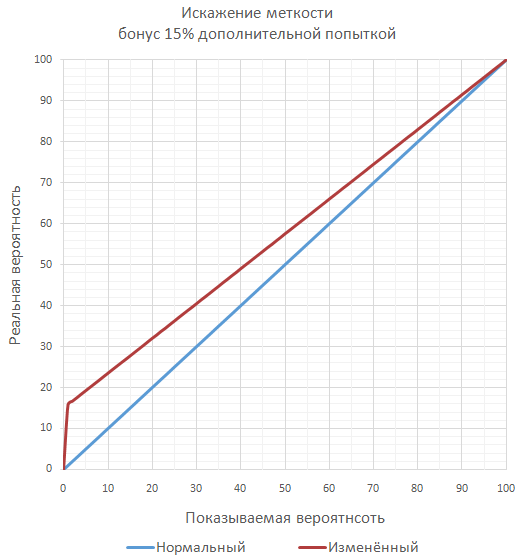
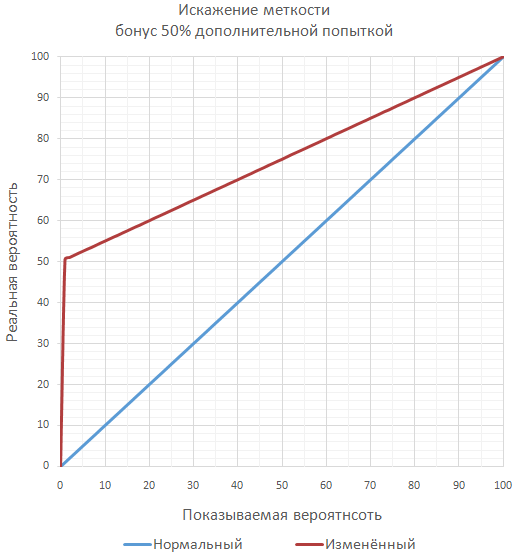
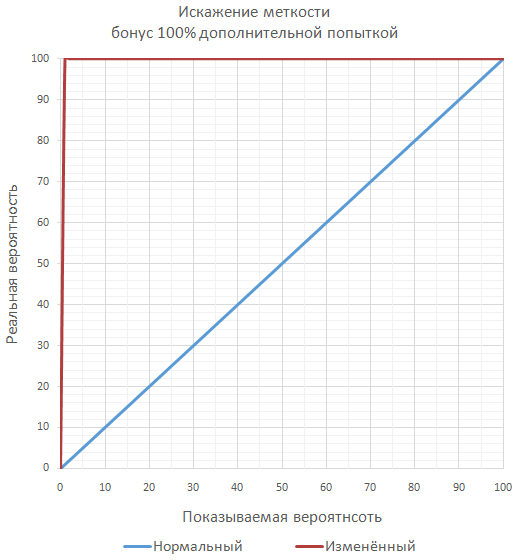
A little exotic is the approach to change the essence of the bonus to accuracy on the bonus of reducing the probability of a miss .
Ensures that there is always a chance of a miss with any bonus. Because of this, the game can give bonuses to the "accuracy" of more than 100%, at least 1000%. And still there will be a chance of a miss. But the player is more likely to confuse, and, therefore, disappoint.
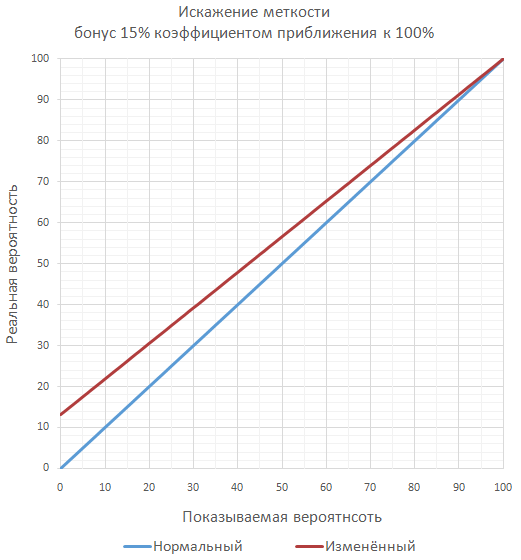
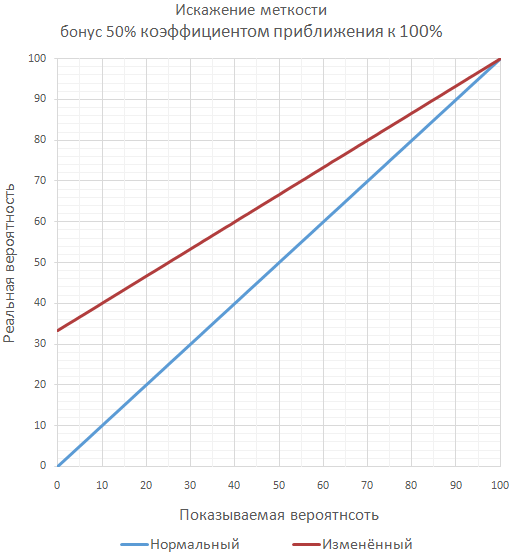
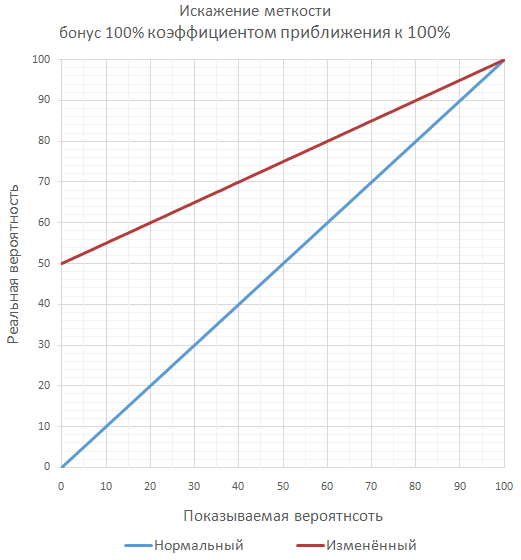
The most commonly used approach is simple summation of bonuses, as the most understandable for the player, and easy to implement by the developer.
This item is based entirely on the visual data of the publication “ Probability and Games: Damage Rolls from Red Blob Games [6] ”. Here I briefly present some examples and conclusions of this publication. In the original article you will receive more detailed conclusions and interactive graphics of distributions, as well as interactively customizable functions for the selection of various unique combinations.
The most obvious (but not the only) example of various damage calculation is presented by calculating damage with a maximum value of 12. The result can be obtained using different dice ( for example, if you play a board game and you don’t have any special dice ):
1d12 - one cube with 12 faces

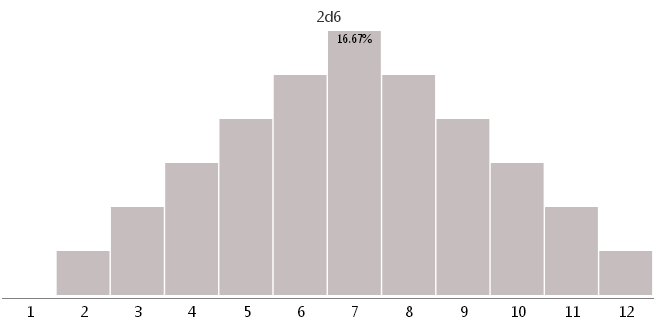
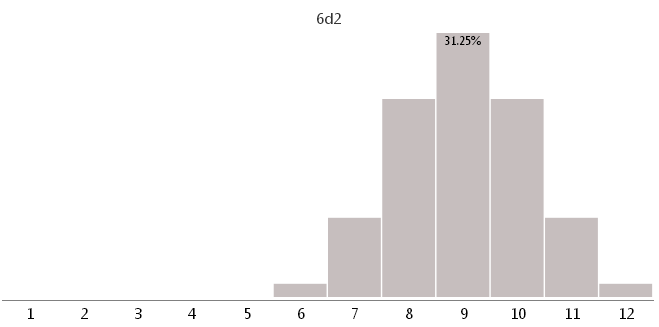
2d6 - two dice with 6 different faces
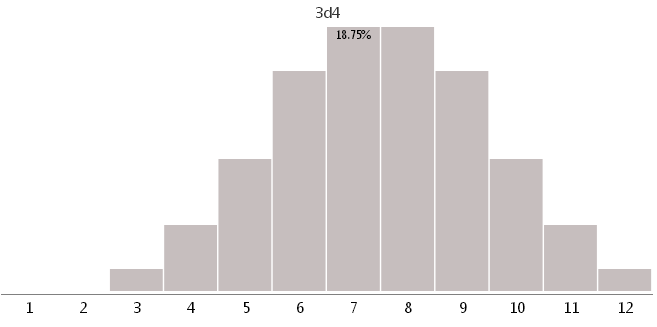
3d4 - three dice with 4 different faces
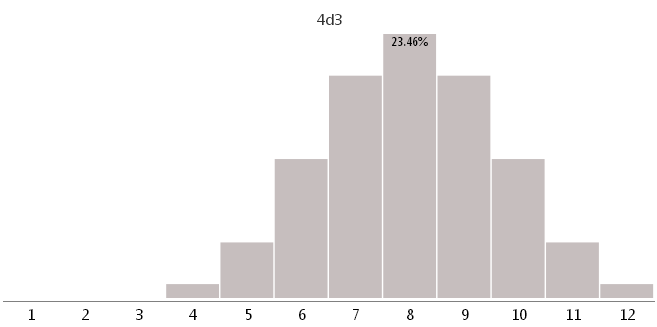
4d3 - four dice with 3 different faces
6d2 - six dice with 2 different faces
As you can see, the use of unsuitable cubes can greatly change the game balance.
Thus, the following topics were addressed:
Each of the methods may be useful to the developer. For games with a more casual audience, more often sparing algorithms are chosen in which the player’s success rate is overestimated, and to raise excitement an illusion of an unlikely victory is created (for more details in one of the previous articles: [ 7 ]).
1. Misconceptions of players in the risk assessment. Control of a random number generator in development .
2. Fire Emblem Wiki - Random Number Generator .
3. Neverwinter Nights 2 - Class Abilities - Slippery Mind .
4. Neverwinter Nights - Pixie Warrior .
5. “Not So Random Randomness” in Game Design and Programming .
6. Probability and Games: Damage Rolls from Red Blob Games .
7. Generation of Close call in games: “On the line from defeat” or “A little bit won” .
- comparing with one pseudo-random number (which can also be obtained differently [ 1 ]);
- comparing with the largest or smallest of two pseudo-random numbers;
- comparing the average of two or more random numbers (the average can also be considered in different ways).

Accuracy bonuses can also be implemented in different ways, thereby causing players irritation for various reasons.
Similarly, the damage done can be calculated in different ways, especially on the basis of dices (cubes).
All these different approaches affect the gameplay: its complexity and predictability. Each of them can be a good solution depending on the goals pursued, therefore it is most advantageous to make a choice consciously.
The article will present visual graphs of changes in real probabilities in different approaches, which will allow them to quickly navigate and make the best decision.
Manipulation with accuracy
Usually, when a player is informed that a character’s accuracy is 60%, he perceives this information as: “I can count on 6 hits out of 10 shots”. And if out of 10 hits he will observe 1 hit instead of 6, then he will almost certainly consider that the accident in the game is broken. He will be especially sure of this if this happens on a segment of 100 shots. In order to avoid such troubles, developers often covertly manipulate with a real probability of hitting ( or refuse from the element of randomness altogether ).
For example, in the game Fire Emblem: The Binding Blade, to determine hit with accuracy, not one random number was compared, but the average of two random numbers [ 2 ].

The result of this manipulation is that well-aimed attacks (> 50%) are hit much more often than they are supposed to be if they are evenly distributed, and non-targeted attacks (<50%) are hit much less often. This is how this probability distribution changes:

For example, with 10% accuracy shown, the actual is 1.9%. And at 75%, the actual will be 87.24%.
But, for that matter, the accuracy can be changed in many other ways.
For example, you can take an average of 3 random numbers:

The distortion resulting from this becomes even more striking: accuracy of 10% becomes 0.41%; accuracy of 75% becomes 92.69%.
However, the average can be calculated as the geometric average. Here are the changes with an average geometric of 2 random numbers:

Here 10% is converted to 4.83%, and 75% to 88.18%. But, most interestingly, the transition occurs at 30%, and not at 50%, as the arithmetic average. Therefore, if you really want to be sure that the player will always have an advantage, it is enough to make sure that his minimum accuracy will never be lower than 30%, and for enemies it will be so low quite often ( for enemies you can use the arithmetic average or something more distorted ).
The geometric mean of 3 numbers leads to approximately the same results, but only with a large scatter:

Here 10% is converted to 1.95%, and 75% to 93.98%.
Often, to enhance or weaken some skills, a simpler manipulation is introduced, when one of the two or two of the random numbers is chosen as the smallest:

As a result, the probability of hitting changes very much. For example, if you select the smallest number, 10% accuracy is converted to 19.02%, and 75% accuracy to 93.75%.
This method, for example, is used in the game “Neverwinter Nights” in the skill “Slippery Mind”, in which in case of failure of the salvage check, a repeated check for willpower is performed [ 3 ].

Below is a table of distortion of accuracy with different methods of calculation.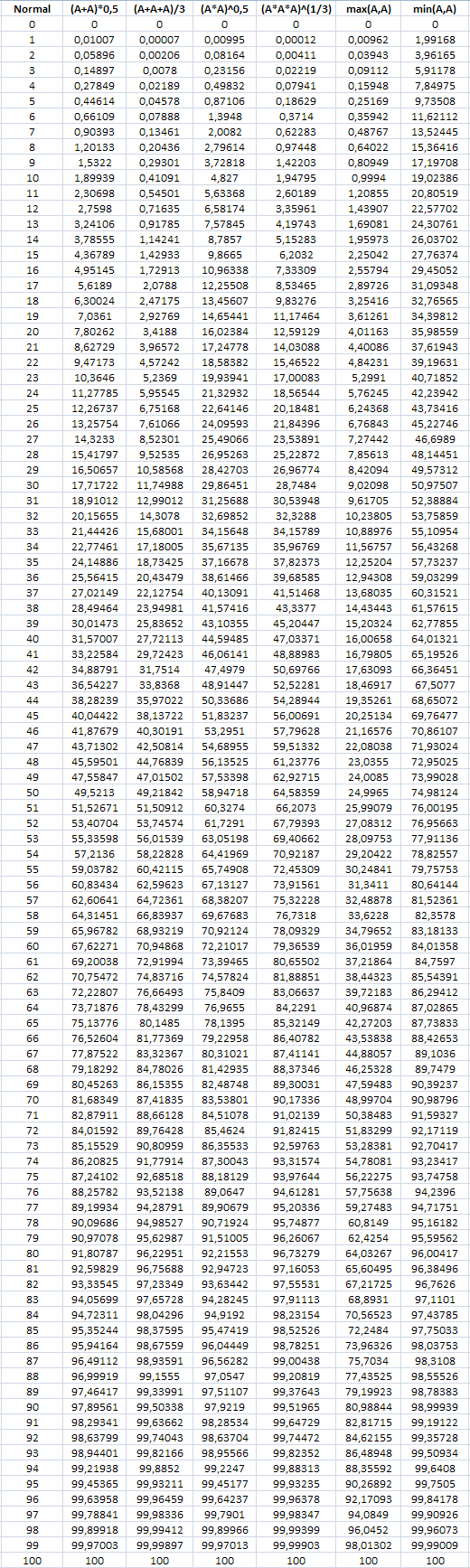

In the last article about manipulations with probabilities, a method was shown for very rare events where the probability of an event increased over time:
Developer Carsten Germer uses the function of controlled randomness for rare and not only events [ 5 ]. For example, in order to guarantee the occasional loss of a particularly rare bonus with a chance of 1 to 10,000, after each “miss” it increases the odds in order: 1 to 9900; 1 to 9800; 1 to 9700 ... and so on until the event was recorded. And in order to guarantee the absence of frequent rarities, he introduced an additional variable blocking the triggering by 100% for the next 10 checks after the last triggering.Players' misconceptions in risk assessment [ 1 ]
This is how the probability of this rare event changes when using this method:

As you can see, in the end, nothing in common with the probability of 1 to 10,000, but for the purposes of gameplay, this may have been enough. Although it looks more like an unintentional concealment of real probabilities from the developer himself, which can lead to wrong decisions in future program modifications.
Below I also give a change in 1% of the event that it will occur at least once as the number of attempts grows. Distortion algorithm: the first 10 attempts - a guaranteed miss. Then, with each slip, the probability increases by 1% (0.1% and 0.01%) before it hits. Then everything is from the beginning.

However, if your main goal, as a developer, is to ensure that a user in a 1% event does not hit a series of 1000 misses in a row, then it will be easier and more transparent after 200 misses in a row to expose a 100% hit. This will relieve you of the rare perplexities of the players and allow you to leave the program code more concise and friendlier for future improvements.
Different ways of accruing bonuses to accuracy
If there are few bonuses to accuracy in the game and they are easily controlled by the developer, then the easiest way is to use the simplest approach with a linear increase in accuracy by simple addition with the base value . This method is the easiest to introduce into the game and is always understandable to players. With this approach, it is possible to achieve 100% accuracy, which is not always consistent with the plans of the developer.



If the game is planned to have a lot of significant bonuses to accuracy, in order not to get over the guaranteed 100% accuracy, you can calculate the final accuracy as a series of additional throws ( most often unlikely separately ). For example, with a hit of 70% and a bonus of 50%, the final hit chance will be 85%, like checking two consecutive shots when at least one hit is enough.



A little exotic is the approach to change the essence of the bonus to accuracy on the bonus of reducing the probability of a miss .
// newAccuracy - новая меткость в %// baseAccuracy - изначальная меткость в %// bonusAccuracy - бонус к меткости в %let newAccuracy = 100 - ( (1 - baseAccuracy * 0.01) / (1 + bonusAccuracy * 0.01) ) * 100;
Ensures that there is always a chance of a miss with any bonus. Because of this, the game can give bonuses to the "accuracy" of more than 100%, at least 1000%. And still there will be a chance of a miss. But the player is more likely to confuse, and, therefore, disappoint.



The most commonly used approach is simple summation of bonuses, as the most understandable for the player, and easy to implement by the developer.
Dice-based damage distribution
This item is based entirely on the visual data of the publication “ Probability and Games: Damage Rolls from Red Blob Games [6] ”. Here I briefly present some examples and conclusions of this publication. In the original article you will receive more detailed conclusions and interactive graphics of distributions, as well as interactively customizable functions for the selection of various unique combinations.
The most obvious (but not the only) example of various damage calculation is presented by calculating damage with a maximum value of 12. The result can be obtained using different dice ( for example, if you play a board game and you don’t have any special dice ):
1d12 - one cube with 12 faces

2d6 - two dice with 6 different faces

3d4 - three dice with 4 different faces

4d3 - four dice with 3 different faces

6d2 - six dice with 2 different faces

As you can see, the use of unsuitable cubes can greatly change the game balance.
Conclusion
Thus, the following topics were addressed:
- manipulation with accuracy using various ways to check it;
- different methods of charging bonuses to accuracy;
- different dips based damage distribution.
Each of the methods may be useful to the developer. For games with a more casual audience, more often sparing algorithms are chosen in which the player’s success rate is overestimated, and to raise excitement an illusion of an unlikely victory is created (for more details in one of the previous articles: [ 7 ]).
Bibliography
1. Misconceptions of players in the risk assessment. Control of a random number generator in development .
2. Fire Emblem Wiki - Random Number Generator .
3. Neverwinter Nights 2 - Class Abilities - Slippery Mind .
4. Neverwinter Nights - Pixie Warrior .
5. “Not So Random Randomness” in Game Design and Programming .
6. Probability and Games: Damage Rolls from Red Blob Games .
7. Generation of Close call in games: “On the line from defeat” or “A little bit won” .
