Foreword

It is difficult to overestimate the importance of computer modeling in the modern world. A long time ago, the days when the trajectories of launching satellites into near-earth orbit were calculated by a crowd of female calculators with Felixes at the ready (there was such a computer ). Today, a modest sized box near your desktop solves all conceivable and unimaginable tasks. But there is one “but.”



The state of engineering education, I do not know how it is in the capitals, but here, on the periphery, looks depressing in the context of this issue. The blame here is the approach to teaching such disciplines at universities as "Numerical methods for solving engineering problems on computers", "Mathematical modeling in%, write yourself%,% and others." This misfortune of engineering education stems from the fact that in courses like these, interdisciplinary connections are sometimes cut off altogether. The learner does not have a chain in his head: fundamental theory -> practical application -> tool for solving the problem.

My idea has long been ripe for writing a cycle in which everything that we call modern mathematical modeling will be sorted into shelves. But to do this is simple and affordable for those who are just beginning to learn this immense discipline of modern science. It is not known what will come of this, but I invite those who are interested in it under cat.

1. The mathematical principles of natural philosophy

Yes, we will start with the mechanics. The science of the pre-Newton era, in the modern sense, was inferior. It lacked a clear, universal methodology for scientific research. But this does not mean that science did not exist. A huge layer of experimental data from different spheres of human activity has been accumulated. Scientists have solved complex problems, often using methods whose genius is still striking. But the brilliant discoveries were episodic in nature. Until a man appeared who wrote the work, which gave scientists a clear mathematical apparatus, which became centuries ago the main tool of scientific knowledge.

It is the " Beginning ..."Newton, who laid the foundations of differential calculus with a practical approach to mechanics, made the latter the first in the history of this scientific theory. The laws of mechanics, somewhere successful, somewhere not very, began to try to explain all the phenomena that occur in nature, from optics to electricity , from thermodynamics to the structure of matter. Time has dotted the “i”, other theories have replaced the mechanistic principles, and mechanics themselves have pretty much evolved. But at the same time, mechanics, like no other discipline, is clear and Detailed Info illustrates all the things, which we shall discuss below Most of the examples in this series will be one way or another connected with the simulation of mechanical systems, at least in his first articles..

Before we begin, I need to give some explanatory comments:

1. The reader should be familiar with the main content of the course of mathematics, understand what vector quantities are. Well, no way. I will try to provide the text with links for a detailed study of bottlenecks, but I will not go into details
   
2. As a tool for performing numerical calculations, we will rely on the GNU Octave package . Why are two reasons. It is free, is an analogue of Matlab and contains everything you need for our purposes. The second reason - I myself want to meet him, so let this be my whim)
   
3. The author is waiting for comments on the material presented in any form, be it comments, letters, etc. This will help make the material better.
   

2. Quantitative parameters describing the movement

Mechanics is a science that studies the movement of material bodies. By mechanical movement is meant the movement of a body in space over time. This definition should lead you to the following questions:

1. What is meant by the body?
2. How to determine its position in space?

By the body, in the scientific and philosophical sense, it is customary to understand any material object, but this vague definition is clearly not enough. Therefore, mechanics operate with the following abstract concepts:

1. Material point (or simply “point”)
2. Absolutely solid (or simply “solid”)

By a point it is customary to understand a body whose dimensions are neglected in specific traffic conditions. To make it clear, let's look from the position of this definition on our planet, the



Earth moving around the Sun has a diameter of about 13,000 kilometers. The sun is almost one and a half million kilometers. Wow points! But here the distance between them is 150 million kilometers, and the path traveled by the Earth in a year in orbit is about a billion kilometers. As you can see, on such a scale of space, the Earth and the Sun can really be considered points.

And if we want to study the rotation of the Earth around its axis?



Then each point of the Earth moves along its own trajectory with respect to the axis of rotation and its size cannot be neglected! Here the Earth should be considered already as a set of connected points or a solid.

Thus, mechanics does not provide us with the body itself, but its two simple models, using which you can solve most practical problems with the degree of accuracy you need in practice.

It makes no sense to talk about a solid body without understanding how the movement of a point is described. Obviously, in order to determine the position of a point in space, it is necessary to choose a reference point, for example, another point. Having decided on the starting point, you need to select those parameters, the quantitative value of which will make it possible to assess the position in space of the moving point of interest to us. Depending on which parameters are selected, I distinguish three ways to specify the movement of a point

2.1. Vector way to set motion

Everything is very simple - a vector is drawn from the origin of coordinates O to point M. The length and direction of this vector allow us to judge where the point is located.



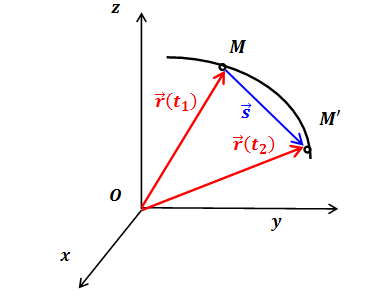
The point will move in space, the vector will change its length and direction, and its end will draw an imaginary curve in space, which is called the trajectory of the point. The vector itself is called the radius vector of the point. If we know the mathematical law, the formula by which we can calculate this vector for any moment in time, then we know the law of motion of the point

$$

This entry tells us that the radius vector is a function of time.

2.2. Coordinate way of setting point motion

We can draw three mutually perpendicular axes x, y, and z from the origin. Then the position of the point will be determined by three numbers - the coordinates in the Cartesian system.



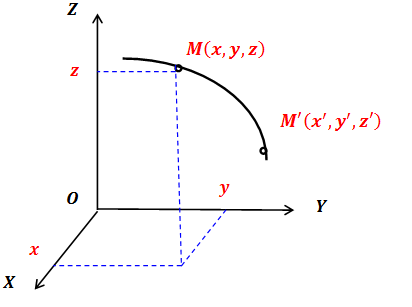
In this case, the law of motion of a point is three functions of time

$$

and now they are already the law of motion.

2.3. The natural (trajectory) way of setting the motion of a point

We may not use vectors and axes at all. We choose the beginning of the report on the point’s trajectory, and estimate the position of the point by the length of the arc that it went along the trajectory.



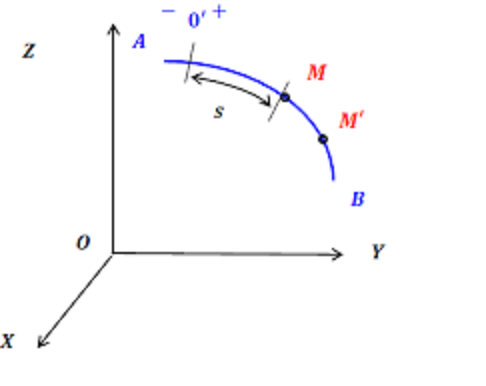
In this case, we will have to determine in which direction along the curve the coordinate s is counted in the positive direction and then the function

$$

it is also the law of motion. This method is convenient when we know exactly the shape of the trajectory of a point.

3. Speed ​​and acceleration

Point speed is the first time derivative of the point vector radius

$$

The velocity vector is directed tangent to the trajectory of the point.

Which, from many points of view, is the most correct and complete definition. If the point motion is specified in a coordinate way, then the velocity vector is determined by its projections on the coordinate axis, calculated as derivatives of the corresponding coordinates

$$

The last designation of a derivative is a dot over a function, as ancient as the “Beginnings ...” themselves and goes back to Newton. It was he who proposed this designation. Then the barcode familiar to schoolchildren and students took root, as a designation of a derivative with respect to an arbitrary parameter, and the dot remained as a designation of a derivative taken precisely with respect to time.

Point acceleration is the first derivative of the point velocity vector, or the second derivative of the point radius vector

$$

In Cartesian coordinates, it looks like this

$$

Here, two points above the functions indicate the second time derivative.

Thus, knowing the law of motion of a point, we can easily determine its speed and acceleration by simple calculation of the derivative.

4. Axioms of dynamics

At school, they talk about Newton's laws. Moreover, they often make a fundamental mistake - they forget to say that these laws are formulated and are valid exclusively for the material point. And they don’t work at all for a solid body (quieter, quieter, no angry exclamations, I will explain everything).

In such a scientific discipline as theoretical mechanics, Newton's laws are usually called axioms, and supplemented by the principle of independence of the action of forces, they form a system of axioms of dynamics.

Axiom 1 (Newton's First Law)

A point moves uniformly and rectilinearly in space if the vector sum of the forces applied to it is zero.

As a mechanics teacher with pretty good experience, I prefer this formulation of the principle of inertia of classical mechanics to the confused school one "there are such reference systems with respect to which blah blah blah ...". It is immediately clear from this formulation: for a mechanical movement to take place, the action of force is absolutely optional. If there are no forces, or their action on the point is compensated, then its movement will occur by inertia, in a straight line with a constant speed. For the direction and magnitude of the speed to change, you need a reason, namely

Axiom 2 (Newton’s Second Law)

The acceleration vector of a point multiplied by its mass is equal to the force acting on the point

$$

If a point is affected by a force other than zero, then it gives rise to acceleration directed in the same direction. And with the advent of acceleration, the speed of the point also changes, which means the nature of the movement.

Axiom 3 (Newton’s Third Law)

Two points interact with forces equal in magnitude, opposite in direction and directed along one straight line.

$$

The fundamental nature of this law can hardly be overestimated, but its deep meaning can be understood using examples that we will not discuss now. So far, I propose to delve into the memory and re-read the school textbook. The following is much more important for us.

Axiom 4 (Principle of independence of the action of forces)

If several forces act on a point, then the acceleration communicated to the point by these forces is equal to the geometric sum of the accelerations communicated to the point by each force individually

It follows that when several forces are applied to a point, the equation

$$

which in mechanics I call a proud and terrible name - the differential equation of motion of a point in vector form.

It is this equation that serves as the starting point for mathematical modeling in mechanics. Solving precisely this equation, we will begin to master the basics of mathematical modeling as an independent scientific branch. Look at it carefully, dig into the memory, open the textbooks. We will remember him more than once.

Now I’ll explain what I meant by saying that Newton’s laws are valid only for the material point. This is true, imagine a rigid body moving in space. Damn it, go outside, pick up a bigger stick from the ground and throw it away. See? Each point of the stick moves along its path. So at every point of the stickyour own acceleration . To which of these points does Newton's second law apply? It applies to every point of the stick, but not to the stick as a whole. The concepts “stick acceleration”, “stick trajectory” are meaningless. It makes sense to accelerate and trajectory of a particular point of the stick, for example its center of mass.

That is why, when describing the motion of a rigid body, they use the theorems of dynamics for a solid: the theorem on the motion of the center of mass, the theorem on the change in the angular momentum and the theorem on the change in kinetic energy. Yes, these theorems are deduced based on the above axioms (Newton's laws). But directly these laws are not applicable to the description of the motion of a rigid body. For the point only.

5. Differential equations of motion of a point

So, Newton’s second law and the principle of independence of the action of forces give us a serious mathematical apparatus in the form of an equation connecting the acceleration of a point and the forces acting on that point. If we replace the acceleration, as defined above, with the second time derivative of the point's radius vector, we will see such an expression

$$

It seems to be simple, but in fact it is extremely cool and important. Look - on our left, there is a law of motion (yes, differentiated twice). And on the right is the sum of the forces. Thus, this equation connects the forces applied to a point and the law of motion. So, knowing the law of motion, you can calculate the force that causes it. Or vice versa, knowing the forces applied to the point, find the law of motion.

In the vast majority of cases, this equation is not used directly, but decomposed into three equations in projections on the coordinate axis

$$

6. Tasks of point dynamics

Using the differential equations of motion of a point, two fundamental problems are solved

The first (inverse) problem of dynamics

According to the well-known law of motion of a point, determine the force acting on the point

Let us know the law of motion of a point, given in the form of the dependence of the radius vector on time

$$

Then, it’s enough to take twice the time derivative of this function, multiply the result by the mass, and we will get the force that causes the point to move according to this law

$$

I note that the force obtained in fact is the resultant of all the forces applied to the point, that is, information about the force factors determining the motion is incomplete. But, however, this principle allowed Newton to discover the law of gravity. Today, this problem has been generalized to arbitrary dynamical systems that are completely unrelated to mechanics and is known in control theory as a method of inverse problems of dynamics.

The second (direct) dynamic problem Using the

known forces applied to a point, determine the law of its motion

The forces applied to the point can be added up to obtain the resultant vector. Moreover, this resultant in the general case will depend on time, the position of the point in space and its speed

$$

We got an equation containing an unknown function $$as well as its two derivatives. Such an equation is called differential in mathematics. His solution ultimately boils down to integration - the operation of finding the derivative inverse. Since the equation contains the second derivative of the unknown function, it is a second-order equation, which means that you have to take the integral twice.

The search operation for an integral in orders is more complicated than the derivative search operation. And in the vast majority of cases, the result cannot be expressed through elementary mathematical functions. As our mathematics teacher at the university said: “If you see a bull, you can imagine what cutlets to make of it. But seeing cutlets, you will never be able to reconstruct a bull from them ... ” In my opinion, this bike perfectly reflects the meaning and complexity of reverse operations.

The impossibility of obtaining an analytical solution to many problems led to the appearance of numerical methods, the rapid growth of which occurred in the computer age. On the day when the differential equation of motion was first solved on a computer, it became the birthday of a new branch of knowledge - mathematical modeling.

Conclusion

No need to blame me for reprinting a textbook on mechanics. This text is copyright and aims to review the theoretical foundations, without which there is no sense in talking about modeling as a practical field. Next time we will practice, but let's start as it should from the basics.

Thank you and see you soon!