Regular Expressions: No Magic
- Transfer
The code for this post, like the post itself, is posted on github .
Until recently, regular expressions seemed to me some kind of magic. I couldn’t figure out how to determine if a string matches a given regular expression. And now I get it! The following is a simple regex engine implementation in less than 200 lines of code.
Part 1: Parsing
Specification
Implementing regular expressions completely is a pretty daunting task; worse, she will teach you little. The version we are implementing is enough to study the topic without slipping into a routine. Our regular expression language will support the following:
.- match any character|- complianceabcorcde+- match one or more of the previous pattern*- match 0 or more of the previous pattern(and)- for grouping
Although the options are small, you can create interesting regexs with it, for example,
m (t|n| ) | ballowing you to find subtitles for Star Wars without subtitles for Star Trek, or (..)*to find the set of all lines of even length.Attack plan
We will analyze regular expressions in three stages:
- Parsing (parsing) a regular expression into a syntax tree
- Convert syntax tree to state machine
- State machine analysis for our line
To analyze regular expressions (more on this below) we will use a finite state machine called NFA . At a high level, the NFA will represent our regex. Upon receiving the input, we will move from state to state in the NFA. If we come to a point from which it is impossible to make a valid transition, then the regular expression does not match the string.
This approach was first demonstrated by one of the Unix authors, Ken Thompson. In his 1968 article in CACM magazine, he outlined the principles for implementing a text editor and added this approach as a regular expression interpreter. The only difference is that his article was written in machine code 7094. At that time, everything was much harder.
This algorithm is a simplification of how engines without reverse lookups like RE2 analyze regular expressions in a provably linear time. It is very different from the regex engines from Python and Java, which use reverse lookups. For given input data with small lines, they are executed almost infinitely. Our implementation will be carried out for
O(length(input) * length(expression). My approach roughly matches the strategy outlined by Russ Cox in his awesome post .
Regular Expression Representation
Let's step back and think about how to present a regular expression. Before starting the analysis of the regular expression, we need to transform it into a data structure with which the computer can work. Although strings are linear in structure, regular expressions have a natural hierarchy.
Let's look at the line
abc|(c|(de)). If we left it as a string, then we would have to go back and perform transitions, tracking various sets of brackets when analyzing the expression. One solution is to convert it to a tree that the computer can easily bypass. For example, it b+awill turn into the following: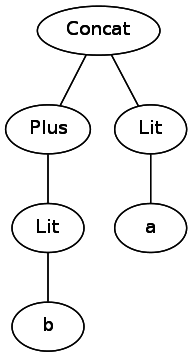
To represent a tree, we need to create a class hierarchy. For example, our class
Orshould have two subtrees representing both sides of it. From the specification it is clear that we need to identify four different components of regular expressions: +, *, |and character literals like ., aand b. In addition, we also need to represent cases when one expression follows another. Here are our classes:abstract class RegexExpr
// ., a, b
case class Literal(c: Char) extends RegexExpr
// a|b
case class Or(expr1: RegexExpr, expr2: RegexExpr) extends RegexExpr
// ab -> Concat(a,b); abc -> Concat(a, Concat(b, c))
case class Concat(first: RegexExpr, second: RegexExpr) extends RegexExpr
// a*
case class Repeat(expr: RegexExpr) extends RegexExpr
// a+
case class Plus(expr: RegexExpr) extends RegexExprRegular expression parsing
To move from a string to a tree view, we need to use the conversion process known as parsing (parsing) . I will not talk in detail about building parsers. Instead, I will outline information that is enough to point you in the right direction if you decide to write your own. I will briefly talk about how to parse regular expressions using the parser combinator library Scala.
The Scala parser library allows us to write a parser by simply writing a set of rules that describe our language . Unfortunately, it uses a lot of stupid characters, but I hope you can get through the noise and get a general understanding of what is happening.
When implementing the parser, we need to determine the order of operations. As in arithmetic, PEMDAS is used [approx. trans. P arentheses, E xponents, M ultiplication / D iVision, A ddition / the S ubtraction - mnemonics, allowing to remember the order of performing arithmetic operations] , as well as its own set of rules used in regular expressions. We can express this more formally with the help of the idea of “linking” the operator to the symbol next to it. Different operators are “bound” with different strengths - by analogy, in expressions like 5 + 6 * 4 the operator is
*bound more than +. In regular expressions, it *binds stronger than|. One could imagine this in the form of a tree in which the weakest operators are at the top.
Therefore, we must be the first to parse the weakest operators, followed by the stronger operators. With parsing, this can be thought of as extracting an operator, adding it to the tree, and then recursively processing the remaining two parts of the string.
In regular expressions, the binding strength is of the following order:
- Character literals and parentheses
+and*- Concatenation - a follows b
|
Since we have four levels of binding forces, we need four different types of expressions. We called them (rather arbitrarily)
lit, lowExpr( +, *) midExpr(concatenation) and highExpr( |). Let's move on to the code. First, we will create a parser for the most basic level, for a single character:object RegexParser extends RegexParsers {
def charLit: Parser[RegexExpr] = ("""\w""".r | ".") ^^ {
char => Literal(char.head)
}Let's take a moment to explain the syntax. The code defines the parser that collects
RegexExpr. The right side says: “Find something that matches \w(any word symbol) or point. If you find it, turn it into Literal. " The brackets should be defined at the lowest level of the parser, because they have the strongest binding. However, we need to be able to put something in brackets. We can achieve this with the following code:
def parenExpr: Parser[RegexExpr] = "(" ~> highExpr <~ ")"
def lit: Parser[RegexExpr] = charLit | parenExprHere we define
*and +: def repeat: Parser[RegexExpr] = lit <~ "*"
^^ { case l => Repeat(l) }
def plus: Parser[RegexExpr] = lit <~ "+"
^^ { case p => Plus(p) }
def lowExpr: Parser[RegexExpr] = repeat | plus | litNext we define the next level - concatenation:
def concat: Parser[RegexExpr] = rep(lowExpr)
^^ { case list => listToConcat(list)}
def midExpr: Parser[RegexExpr] = concat | lowExprFinally, we define “or”:
def or: Parser[RegexExpr] = midExpr ~ "|" ~ midExpr
^^ { case l ~ "|" ~ r => Or(l, r)}And in the end we will determine
highExpr. highExpr- this oris the weakest binding operator, or if not or, then midExpr. def highExpr: Parser[RegexExpr] = or | midExprNext, add some helper code to finish:
def listToConcat(list: List[RegexExpr]): RegexExpr = list match {
case head :: Nil => head
case head :: rest => Concat(head, listToConcat(rest))
}
def apply(input: String): Option[RegexExpr] = {
parseAll(highExpr, input) match {
case Success(result, _) => Some(result)
case failure : NoSuccess => None
}
}
}And that is all! If you take this code in Scala, you can generate syntax trees for any regular expression that satisfies the specification. The resulting data structures will be trees.
Now that we can transform our regular expressions into syntax trees, we are approaching to parse them.
Part 2: Generating NFA
Convert syntax tree to NFA
In the previous part, we transformed a flat-line representation of a regular expression into a hierarchical syntax tree form. In this part, we will transform the syntax tree into a state machine. The state machine takes the regex components in a linear form of the graph, creating the relationship “a follows b follows c”. A graph representation will simplify the analysis with respect to the potential row.
Why do another conversion just to match regex?
Of course, one could do the conversion directly from the string to the state machine. You can even try to parse a regular expression directly from the syntax tree or from a string. However, you will have to deal with much more complex code. By slowly lowering the level of abstraction, we can ensure that the code is easy to understand at every stage. This is especially important when building something similar to a regular expression interpreter with almost infinite borderline cases.
NFA, DFA and you
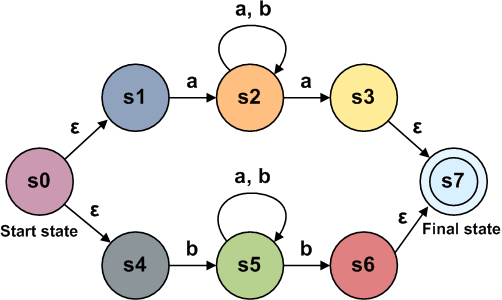
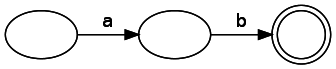
We will create a state machine called NFA, or nondeterministic finite automata . It has two types of components: states and transitions. When presented in the diagram, states are indicated by circles, and transitions are indicated by arrows. The match state is indicated by a double circle. If a transition is marked, it means that we must get this symbol at the input in order to make this transition. Transitions may also not have tags. This means that we can make the transition without consuming input. Note: in the literature this is sometimes referred to as ε. A state machine representing a simple regex “ab”:
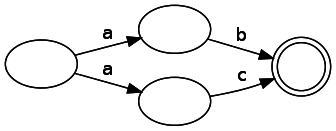
Our nodes may have several correct subsequent states for a given input, since the diagram below shows two paths that consume the same input when switching from a node:
Compare this to a deterministic finite state machine (DFA), in which, as its name implies, given input can lead to a single state change. On the one hand, this reduction in restrictions makes analysis a little more complicated, but on the other hand, as we will soon see, it greatly simplifies generating them from a tree. Fundamentally, NFAs and DFAs are similar to each other in the state machines they can represent.
Transformation in theory
Let's outline a strategy for converting a syntax tree to an NFA. Although this may seem intimidating, you will see that breaking the process down into composable fragments will make it easy to understand. Recall the syntax elements that we need to convert:
- Character literals:
Lit(c: Char) *:Repeat(r: RegexExpr)+:Plus(r: RegexExpr)- Concatenation:
Concat(первая: RegexExpr, вторая: RegexExpr) |:Or(a: RegexExpr, b: RegexExpr)
Subsequent transformations were originally set forth by Thompson in his 1968 article. In the conversion schemes, it
Inwill refer to the entry point of the state machine, and Out- to the output. In practice, they can be a Match state, a Start state, or other regex components. The abstraction In/ Outallows us to compose and combine finite state machines - the most important conclusion. We will apply this principle in a more general sense to transform from each element of the syntax tree into a composable finite state machine. Let's start with character literals. A character literal is a transition from one state to another that consumes input data. The consumption of the literal “a” will look like this:
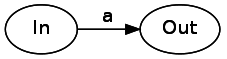
Next, let's explore concatenation. To concatenate the two components of the syntax tree, we just need to connect them with an arrow without labels. It is worth noting that in this example, as it
Concatmay contain the concatenation of two arbitrary regular expressions, so Awith Bthe scheme can be finite state machines, and not just separate states. Something a bit strange happens if and A, and Bboth are literals. How do we connect two arrows without intermediate states? The answer is that literals can have phantom states on both sides to preserve the integrity of the state machine. Concat(A, B)converts to the following:
Чтобы представить
Or(A, B), нам необходимо выполнить ветвление из начального состояния в два отдельных состояния. После завершения этих автоматов они оба должны указывать на последующее состояние (Out):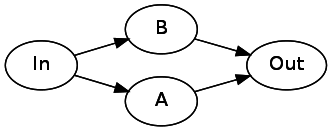
Давайте рассмотрим
*. Звёздочка может быть 0 или более повторений паттерна. Чтобы реализовать это, нам нужно, чтобы одно соединение указывало непосредственно на следующее состояние, а одно возвращалось назад к текущему состоянию через A. A* будет выглядеть так: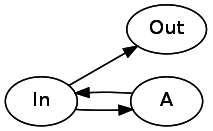
For
+we will use a little trick. a+- it's that simple aa*. Summarizing, you can rewrite Plus(A)how Concat(A, Repeat(A)). We will do so, instead of developing a special pattern for this case. I had a special reason for inclusion in the language +: I wanted to show how other, more complex elements of regular expressions that I missed can often be expressed in categories of our language.Conversion to practice
Now that we have a theoretical plan, let's figure out how to implement it in code. We will create a mutable graph to store our tree. Although I prefer immutability, creating immutable graphs is annoying in its complexity, and I'm lazy.
If we try to reduce the above schemes to basic components, then as a result we get three types of components: arrows that consume input data, a state of coincidence, and one state that splits into two states. I know this looks a little strange, and potentially incomplete. You just have to trust me that such a solution will lead to the cleanest code. Here are our three classes of NFA components:
abstract class State
class Consume(val c: Char, val out: State) extends State
class Split(val out1: State, val out2: State) extends State
case class Match() extends StateNote: I did
Matchcase-классомinstead of the regular class. Case classes in Scala give the class convenient features by default. I used it because it gives equivalence based on values. This makes all objects Matchequivalent - a useful property. For other types of NFA components, we need link equivalence. Our code will recursively traverse the syntax tree, saving the object as a parameter
andThen. andThen- this is what we will attach to the free exits of our expression. It is required because in an arbitrary branch of the syntax tree there is not enough context of what will happen next - andThenit allows us to pass this context down during a recursive traversal. It also provides us with an easy way to join state Match.When it comes to processing
Repeat, we have a problem. andThenfor Repeatitself is a splitting operator. To deal with this problem, we will introduce a placeholder, which will allow us to bind it later. We will represent the placeholder in the following class:class Placeholder(var pointingTo: State) extends Statevarin Placeholdermeans that is pointingTomutable. This is an isolated part of mutability, allowing us to conveniently create a cyclic graph. All other members are unchanged. Let's start with what
andThenis Match(). This means that we will create a state machine corresponding to our Regex, which can then go into a state Matchwithout consuming incoming data. The code will be short but rich: object NFA {
def regexToNFA(regex: RegexExpr): State =
regexToNFA(regex, Match())
private def regexToNFA(regex: RegexExpr,
andThen: State): State = {
regex match {
case Literal(c) => new Consume(c, andThen)
case Concat(first, second) => {
// Сначала first в NFA. Её "выход"
// будет результатом преобразования second в NFA.
regexToNFA(first, regexToNFA(second, andThen))
}
case Or(l, r) => new Split(
regexToNFA(l, andThen),
regexToNFA(r, andThen)
)
case Repeat(r) =>
val placeholder = new Placeholder(null)
val split = new Split(
// Один путь ведёт к заполнителю,
// а другой - обратно к r
regexToNFA(r, placeholder),
andThen
)
placeholder.pointingTo = split
placeholder
case Plus(r) =>
regexToNFA(Concat(r, Repeat(r)), andThen)
}
}
}And that is all! The ratio of sentences to lines of code in this part is quite high - each line encodes a lot of information, but it all comes down to the transformations discussed in the previous part. It is worth explaining - I did not just sit down and write down the code in this form; brevity and functionality of the code were the result of several iterations of working with data structures and the algorithm. Pure code is hard to write.
During the debugging process, I wrote a short script to generate files
dotfrom the NFA, so that you can see the generated NFAs for debugging purposes. It is worth noting that the NFAs generated by this code contain many unnecessary transitions and states. When writing an article, I tried to make the code as simple as possible, even at the cost of performance. Here are some examples of simple regular expressions:(..)*
ab
a|b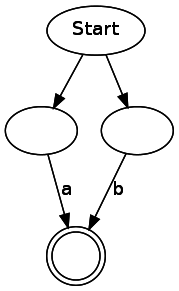
Now that we have the NFA (the hardest part), we just have to analyze it (the part is easier).
Part 3: NFA Analysis
NFA, DFA, and Regular Expressions
In the second part, we said that there are two types of finite state machines: deterministic and nondeterministic. They have one key difference: a non-deterministic finite state machine can have several paths to one node for one token; in addition, the paths can be followed without receiving input. In terms of expressive capabilities (often called “power”), NFAs, DFAs, and regular expressions are similar. This means that if you can express a rule or pattern (for example, even-length strings) using NFA, you can also express it through DFA or regular expression. Let's first look at the regex
abc*expressed as DFA:
DFA analysis is straightforward - we simply move from state to state by consuming an input string. If we finish consuming input in a match state, then we have a match, otherwise it is not. Our state machine, on the other hand, is NFA. The NFA generated by our code for this regular expression is as follows:
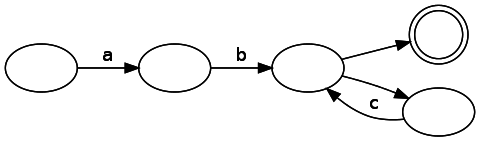
Note that there are several unlabeled edges that can be passed without consuming the symbol. How to track them effectively? The answer is surprisingly simple: instead of tracking only one possible state, you need to store a list of states in which the engine is currently located. When branching occurs, you need to follow both paths (turning one state into two). If the state does not have a valid transition for the current input, then it is removed from the list.
Here you need to consider two subtle points: avoiding infinite loops in the graph and the correct processing of transitions without input data. When analyzing a given state, we first go to all states to list all possible states that are reachable from our current state, if we do not consume more input data. At this stage, you need to be careful and keep the "many visited" to avoid endless looping in the graph. Having enumerated all these states, we consume the next token of input data, either going to these states or removing them from the list.
object NFAEvaluator {
def evaluate(nfa: State, input: String): Boolean =
evaluate(Set(nfa), input)
def evaluate(nfas: Set[State], input: String): Boolean = {
input match {
case "" =>
evaluateStates(nfas, None).exists(_ == Match())
case string =>
evaluate(
evaluateStates(nfas, input.headOption),
string.tail
)
}
}
def evaluateStates(nfas: Set[State],
input: Option[Char]): Set[State] = {
val visitedStates = mutable.Set[State]()
nfas.flatMap { state =>
evaluateState(state, input, visitedStates)
}
}
def evaluateState(currentState: State, input: Option[Char],
visitedStates: mutable.Set[State]): Set[State] = {
if (visitedStates contains currentState) {
Set()
} else {
visitedStates.add(currentState)
currentState match {
case placeholder: Placeholder =>
evaluateState(
placeholder.pointingTo,
input,
visitedStates
)
case consume: Consume =>
if (Some(consume.c) == input
|| consume.c == '.') {
Set(consume.out)
} else {
Set()
}
case s: Split =>
evaluateState(s.out1, input, visitedStates) ++
evaluateState(s.out2, input, visitedStates)
case m: Match =>
if (input.isDefined) Set() else Set(Match())
}
}
}
}And that is all!
Finish the deal
We are done with all the important code, but the API is not as clean as we would like. Now we need to create a single-call user interface to invoke our regular expression engine. We will also add the ability to match the pattern anywhere on the line with the share of syntactic sugar.
object Regex {
def fullMatch(input: String, pattern: String) = {
val parsed = RegexParser(pattern).getOrElse(
throw new RuntimeException("Failed to parse regex")
)
val nfa = NFA.regexToNFA(parsed)
NFAEvaluator.evaluate(nfa, input)
}
def matchAnywhere(input: String, pattern: String) =
fullMatch(input, ".*" + pattern + ".*")
}And here is the code used:
Regex.fullMatch("aaaaab", "a*b") // True
Regex.fullMatch("aaaabc", "a*b") // False
Regex.matchAnywhere("abcde", "cde") // TrueAnd we will end there. Now we have a partially functional regex implementation in just 106 lines. You can add some more details, but I decided not to increase the complexity without increasing the value of the code:
- Character classes
- Retrieving Values
?- Escape characters
- And much more.
Hopefully this simple implementation will help you understand what is going on inside the regex engine! It is worth mentioning that the performance of the interpreter is disgusting, truly terrible. Perhaps in one of the future posts I will analyze the reasons for this and discuss ways to optimize ...
