Selfish Issues: Traffic Jams and the Braes Paradox
- Transfer

The construction of wider roads can worsen the traffic situation. Usually this counterintuitive and counterproductive result is explained as follows: the more roads, the larger shopping centers they attract, which in turn attracts more cars. But this is not the whole story. In the 1960s, Dietrich Braes discovered a theoretical road configuration in which the construction of a new connecting road can slow everyone down, even if the number of cars remains constant. Conversely, closing one road in the Braes network will allow everyone to get home faster. Such a phenomenon is so strange that it deserves its own definition - the Braes Paradox.
Few years ago Joel Cohentold me that the Braes paradox could be a good topic for my column in Computing Science. I doubted. Already published many discussions of this paradox, including the amazing articles of Cohen himself, as well as the book of Tim Rafgarden (a review of which I wrote for the American Scientist ). I did not think that I could add anything new to the discussion.
However, recently I began to consider the task of visualizationBraes' paradox - presenting it in such a way that we can observe individual cars traveling through the road network, and not just calculate average speeds and travel times. The ability to experiment with the model — push levers and buttons, try different routing algorithms — can lead to a clearer understanding of why well-informed and self-interested drivers can choose a route that slows down everyone as a result.
Now I have a working model of something that resembles the Braes paradox, written in JavaScript. I recommend trying to ride on it . There is also an accompanying column “Computing Science” in American Scientist , which is posted on the journal’s website in HTML andA PDF . If you are interested in the source code, then it is on Github . Here I want to talk a little about the implementation of the model and what it taught me.
Adapting Braes' mathematical model to a more mechanistic and visual environment was more difficult than I expected. The original formulation is rather abstract and not particularly physical; it is closer to graph theory than to highway design. In the diagrams below, the wide blue roads labeled A and B are never congested; regardless of the traffic they pass, the travel time on them is always equal to one hour. On narrow red roads a and b , the travel time is zero when they are empty, but traffic increases with increasing load; if all the cars gather on one red road, the driving time on it also becomes equal to one hour. Golden Route X magically provides instant transportation to any number of vehicles.
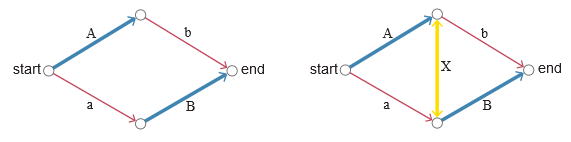
The presence of the paradox depends on the existence of the road the X . Without a gold connection (left diagram), traffic is evenly distributed between the Ab and aB routes , and all cars spend 90 minutes on the whole trip. When you open connection X (right diagram), all drivers prefer the aXb route , and they all spend a full two hours on the road.
A necessary assumption for this paradox is that everyone strives for a selfish route construction, choosing the path that provides the fastest movement, and ignoring all other factors except the time of movement. It is ironic that, insisting that no one else would have a shorter trip, drivers create a tight traffic jam on the aXb route , while the AXB remains empty. Why? If any driver decides to move to AXB , then his absence will slightly reduce the load on aXb , which will give this route a slight advantage in speed. Following selfish aspirations, a driver who has shifted to a different path should return to aXb . It turns out a stalemate.
Cars moving at infinite speed and roads with infinite bandwidth are quite appropriate in the mathematical model, but cause problems in the simulation, which should simulate real traffic on the highway. In search of a more realistic model, I came to the road location shown below, inspired by the diagram from a 1997 article by Claude M. Pinchin (Braess Paradox: maximum penalty in a minimal critical network. Transportation Research A 31 (5): 379–388).

The topology of the circuit is the same as in the original Braes network, but the geometry is different, and therefore the connection between overflow and speed, too. The goal is still to get from start to finish or from Origin to Destination . Road sections A and B are still wide and not subject to traffic jams. Roads a and b are more direct and shorter, but at the same time narrower. With zero traffic, the speed of the machine on a and b is the same as on A and Bbut with increasing load the speed drops. Analogue "golden road" is short at the center of the bridge card, having the same properties as rate as the A to B . In the initial configuration, the bridge is locked, but it can be opened with the click of a mouse. In the screenshot above of the working model, the bridge is open and moving along it.
Cars represented by colored dots enter the system at Origin . At the time of entry, each car selects one of the possible routes. If the bridge is closed, there are only two options: Ab and aB . When the bridge is open, drivers can also choose a shorter road ab or a longer AB. Then the cars move along the selected routes, obeying the speed limits on each segment, until they reach the Destination point .
This scheme differs in some important aspects from the original Braes formulation. Does it show a paradox? In other words, does travel time increase when the bridge is open and drivers can move along the ab and AB routes ? The answer for a wide range of parameter values will be “yes”, and this can be seen from the following results:
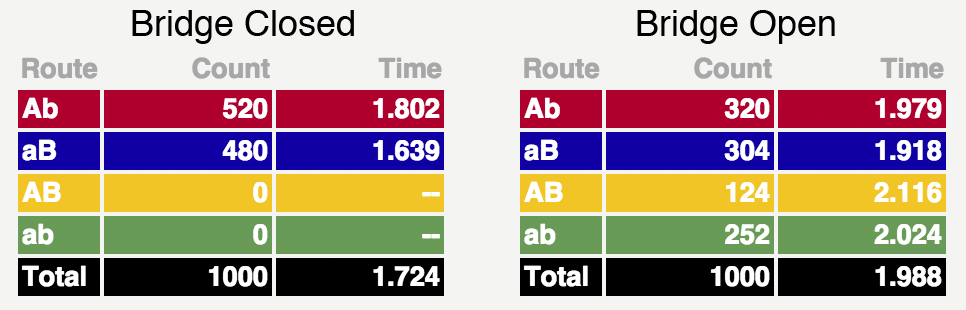
The tables show the number of cars that have chosen each of the routes and the average time they spent on the road. (Time is measured in units of the fastest trip possible: along the shortest path ab with zero traffic.) Note that the opening of the bridge slowed down the speed on all four routes. Even though there was 37% less traffic on Ab and aB routes , cars on these routes needed 9-15% more time to complete the trip. Routes ab and AB were even slower.
But the numbers do not fully reveal the situation - this was the first thing I realized after starting the simulation. In the case of a closed bridge, when the total traffic is divided into two approximately equal flows, it can be assumed that the new cars alternately choose Ab or aB , so that the system reaches a statistically equilibrium state with an equal number of cars on each of the two routes at any given time. But something completely different is happening! It’s best to verify this by running a simulation, but the graph below also gives us a general understanding of the model.
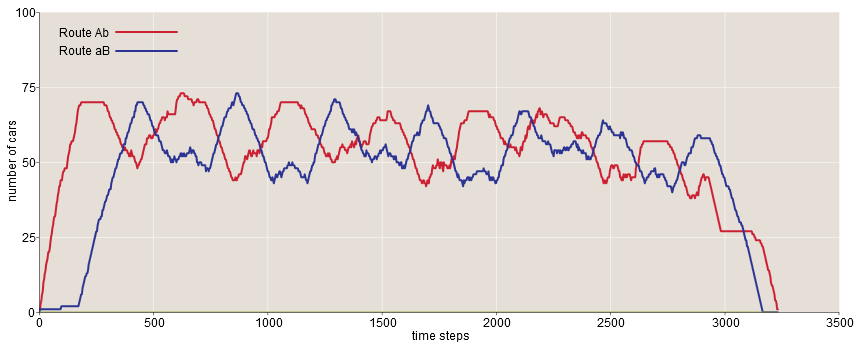
Instead of transitioning to an equilibrium state, the system oscillates with a period of approximately 500 time periods, which is approximately equal to half the time it takes an average car to move from Origin to Destination . The two curves are phase shifted almost exactly 180 degrees.
It is easy to understand where such vibrations come from. When each car enters the road network, it selects the route with the shortest expected travel time based on the current status. The main decisive factor in the expected travel time is the number of cars occupying segments a and bat which speed decreases when roads are full. But when cars choose a less popular route, they also increase the occupancy of this route, which makes it less desirable for cars following them. In addition, there is a significant delay on the Ab route before cars reach the section affected by overflow. The delay and asymmetry of the network creates instability - a feedback loop in which outliers and excessive correction are inevitable.
When the connecting bridge is open, the pattern becomes more complex, but the vibrations are still very noticeable:

It seems that there are two intermittent phases - in one, Ab and ab dominate (in this color scheme, the red-green Christmas phase), in the other, ab and AB (the yellow-green “Boy Scout” phase) prevail. The wave period is less regular, but basically it is longer.
I am not the first to observe such fluctuations; for example, they are mentioned by Daniel Bushema and colleagues in an article describing a simulation of Brales-like road networks in NetLogo . However, in general, little attention is paid to such fluctuations and instabilities in the literature.
The asymmetry of the circuit is very important for creating both oscillations and paradoxical slowdown when opening the central connecting node. You can verify this yourself by running the symmetric version of the model . She turns out to be pretty boring.
Another bug / feature of the dynamic model deserves comment. In the original Braes network, connections A and B have unlimited capacity; in fact, the model promises that the travel time of these roads will be constant, regardless of traffic. In a dynamic model with discrete machines with nonzero dimensions, this promise is difficult to keep. Suppose cars follow route Ab and segment b is completely clogged. At the junction point, where A goes to b , the machines have nowhere to go, so they return back to segment A , which because of this cannot guarantee a constant speed.
When implementing the dynamic model, I found that there are many possible solutions, in the choice of which the mathematical formulation of the original Braes system will not help me much. One of them was the problem of "reverse penetration of the queue." Should cars be allowed to pile up on the road or give them invisible buffers in which they can calmly wait their turn to continue their journey? What about cars appearing in the beginning node when there is no place for them on the roads? Do I need to queue them, drop them, and let them block cars heading along another road? Another slippery moment concerns priorities and honesty. Two nodes near the middle of the road scheme have two entrances and two exits. If there are cars in both lines at the entrance, waiting for passage through the node, which one will move first? If you do not pay attention to the choice of a strategy for processing such traffic jams, then one route will be constantly blocked by another.
Having studied the JavaScript code, you can understand what solutions I chose. I will not say that my answers are absolutely correct. But more importantly, after many experiments and studies of alternative solutions, I found out that most of the details are not so important. The Braes effect is quite stable, it manifests itself in many versions of the model with slightly different assumptions and algorithms. Such stability tells us that we should look more closely at real routes for evidence of paradoxical traffic patterns.
