Anomaly detection in network monitoring data using statistics methods
When there are too many observable metrics, tracking all the graphs on their own becomes impossible. Typically, in this case, tests for critical values are used for less significant metrics. But even if the values are chosen well, some of the problems go unnoticed. What are these problems and how to detect them - under the cut.

Commercial products are almost always presented in the form of a service that uses both statistics and machine learning. Here are some of them: AIMS , Anomaly.io (a great blog with examples), CoScale (the ability to integrate, for example with Zabbix), DataDog , Grok , Metricly.com and Azure (from Microsoft). Elastic has a machine learning - based X-Pack module .
Open-source products that you can deploy at home:
In my opinion, open-source is much inferior in search quality. To understand how the search for anomalies works and whether it is possible to correct the situation, you will have to plunge a little into the statistics. The math details are simplified and hidden under the spoilers.
To analyze the time series, a model is used that reflects the expected features (components) of the series. Typically, a model consists of three components:
You can include additional components, for example, cyclical , as a trend multiplier,
abnormal (Catastrophic event) or social (holidays) . If a trend or seasonality is not visible in the data, then the corresponding components from the model can be excluded.
Depending on how the components of the model are interconnected, its type is determined. So, if all the components add up to get the observed series, then they say that the model is addictive, if it multiplies, then it is multiplicative, if something multiplies, and something mixes up, then it’s mixed. Typically, the type of model is selected by the researcher based on a preliminary analysis of the data.
Having chosen the type of model and the set of components, we can proceed to the decomposition of the time series, i.e. its decomposition into components.
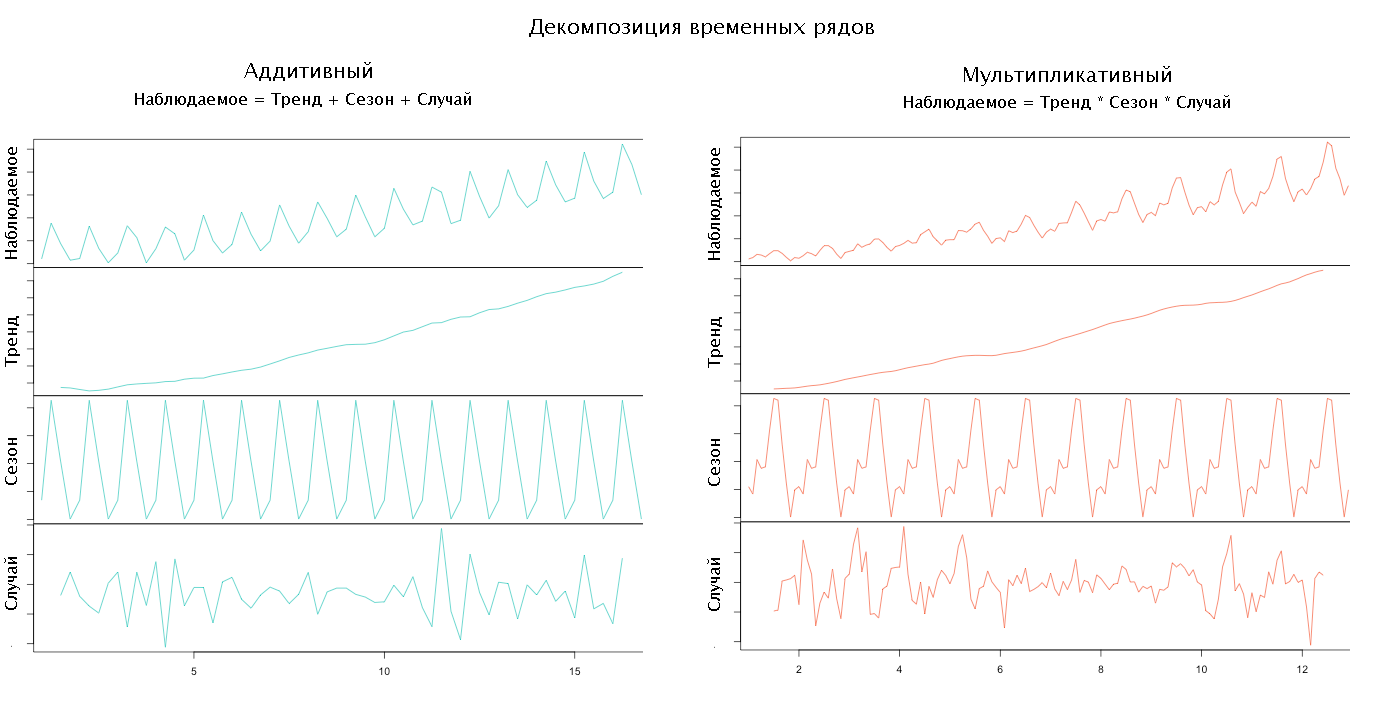
Source Anomaly.io
First, we highlight the trend, smoothing the source data. The method and degree of smoothing are chosen by the researcher.
To determine the seasonal component, we subtract the trend from the initial series or divide by it, depending on the type of the selected model, and smooth it again. Then we divide the data on the length of the season (period), usually this is a week, and we find the average season. If the length of the season is not known, then you can try to find it:
For more information on models and decompositions, see Extract Seasonal & Trend: using decomposition in R and How To Identify Patterns in Time Series Data .
Having removed the trend and the seasonal factor from the initial series, we obtain a random component.
If we analyze only a random component, then many anomalies can be reduced to one of the following cases:
Of course, many algorithms for finding anomalies are already implemented in the R language , intended for statistical data processing, in the form of packages: tsoutliers , strucchange , Twitter Anomaly Detection, and others . Read more about R in articles. Do you already use R in business? and my experience of introducing R. It would seem that connect the packages and use. However, there is a problem - setting the parameters of statistical checks, which, unlike critical values, are far from obvious to most and do not have universal values. The way out of this situation may be their selection by enumeration (resource-intensive), with a rare periodic refinement, independently for each metric. On the other hand, most of the anomalies that are not related to seasonality are well defined visually, which suggests the use of a neural network for rendered graphics.
Below I present my own algorithms that work comparable to Twitter Breakout by results, and somewhat faster in speed when implemented in Java Script.

Disclaimer
Although the author has a mathematical background, he is in no way associated with either Data Mining or statistical analysis. This material is the result of a study conducted to find out the possibility of writing an anomaly search module (even a weak one) for the monitoring system under development.
What we are looking for in two pictures
Chart Anomaly Examples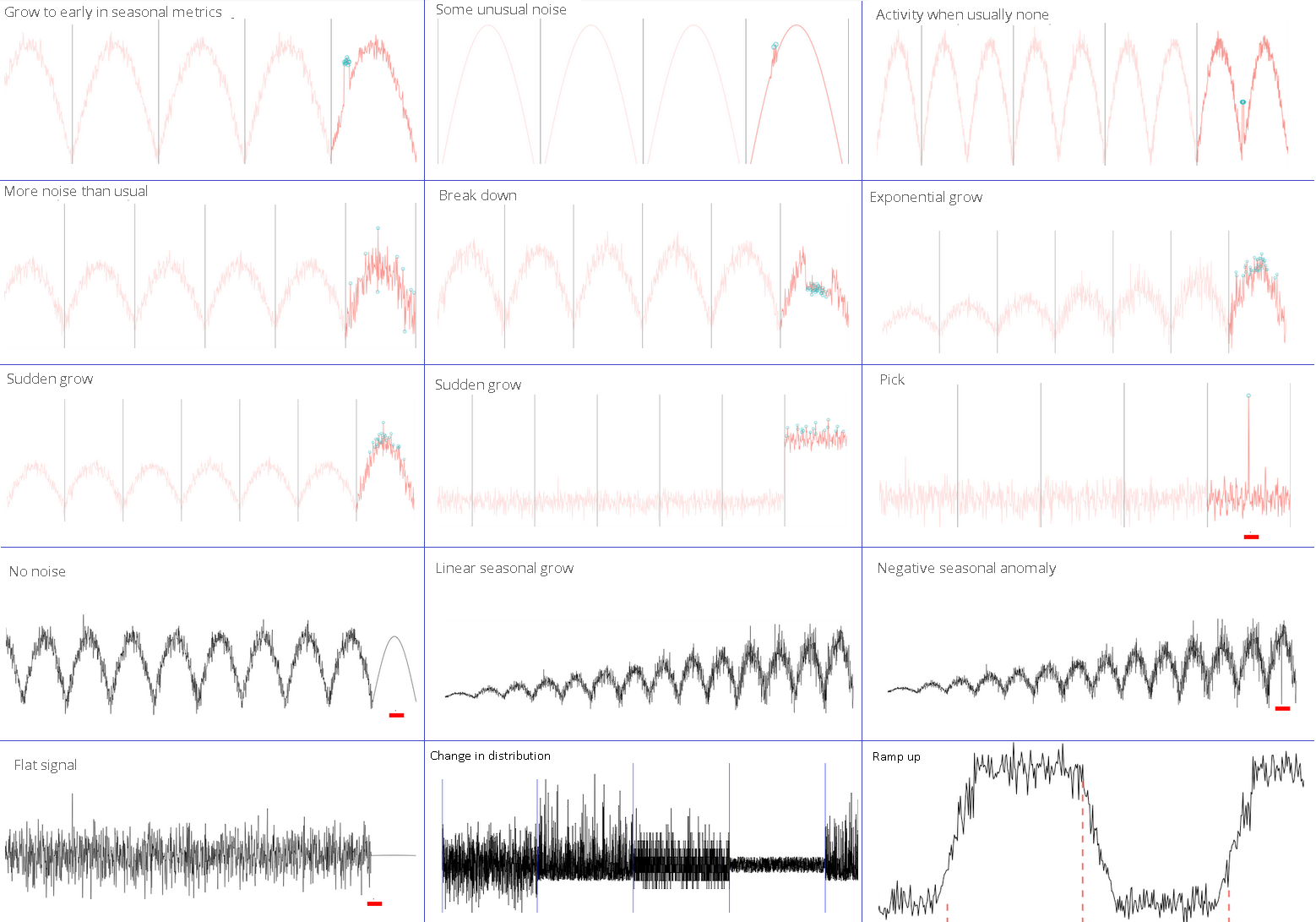
Source Anomaly.io
Of course, in reality, everything is not always so simple: only on b), e) and e) is an obvious anomaly.
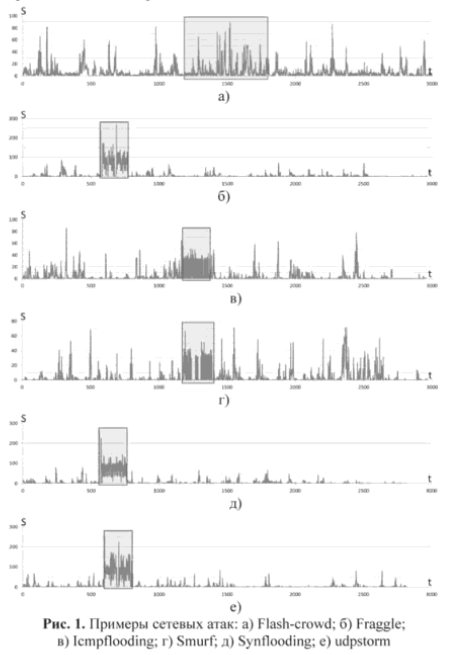
Source cyberleninka.ru

Source Anomaly.io
Of course, in reality, everything is not always so simple: only on b), e) and e) is an obvious anomaly.

Source cyberleninka.ru
Current state of affairs
Commercial products are almost always presented in the form of a service that uses both statistics and machine learning. Here are some of them: AIMS , Anomaly.io (a great blog with examples), CoScale (the ability to integrate, for example with Zabbix), DataDog , Grok , Metricly.com and Azure (from Microsoft). Elastic has a machine learning - based X-Pack module .
Open-source products that you can deploy at home:
- Netflix Atlas is an in-memory time series analysis database. The search is performed by the Holt-Winters method.
- Banshee by Eleme. For detection, only one algorithm is used, based on the three sigma rule.
- Etsy's KALE stack, consisting of two Skyline products , for detecting problems in real time, and Oculus for finding relationships. It seems abandoned.
- Morgoth is an anomaly detection framework in Kapacitor (InfluxDB notification module). Out of the box it has: the three sigma rule, the Kolmogorov-Smirnov test and the Jensen-Shannon deviation .
- Prometheus is a gaining monitoring system in which you can independently implement some search algorithms using standard functionality.
- RRDTool is a database used, for example, in Cacti and Munin. Able to make a prediction using the Holt-Winters method. How this can be used - in the article Forecasting Monitoring, Potential Failure Alerts
- ~ 2000 repositories on GitHub
In my opinion, open-source is much inferior in search quality. To understand how the search for anomalies works and whether it is possible to correct the situation, you will have to plunge a little into the statistics. The math details are simplified and hidden under the spoilers.
Model and its components
To analyze the time series, a model is used that reflects the expected features (components) of the series. Typically, a model consists of three components:
- Trend - reflects the general behavior of the series in terms of increasing or decreasing values.
- Seasonality - periodic fluctuations in values associated, for example, with the day of the week or month.
- A random value is what remains of the series after the exclusion of other components. Here we will look for anomalies.
You can include additional components, for example, cyclical , as a trend multiplier,
abnormal (Catastrophic event) or social (holidays) . If a trend or seasonality is not visible in the data, then the corresponding components from the model can be excluded.
Depending on how the components of the model are interconnected, its type is determined. So, if all the components add up to get the observed series, then they say that the model is addictive, if it multiplies, then it is multiplicative, if something multiplies, and something mixes up, then it’s mixed. Typically, the type of model is selected by the researcher based on a preliminary analysis of the data.
Decomposition
Having chosen the type of model and the set of components, we can proceed to the decomposition of the time series, i.e. its decomposition into components.

Source Anomaly.io
First, we highlight the trend, smoothing the source data. The method and degree of smoothing are chosen by the researcher.
Series Smoothing Methods: Moving Average, Exponential Smoothing, and Regression
The easiest way to smooth the time series is to use half of the neighboring
If you use not one but several previous values, i.e. arithmetic mean of k-neighboring values, then this smoothing is called a simple moving average with a window width k
If for each previous value we use some coefficient of our own, which determines the degree of influence on the current one, then we obtain a weighted moving average .
A slightly different way is exponential smoothing. The smoothed series is calculated as follows: the first element matches the first element of the original series, but the subsequent ones are calculated by the forum
Where α is the smoothing coefficient, from 0 to 1. It is easy to see that the closer α is to 1, the more the resulting series will be similar to the original one.
To determine the linear trend, you can take the methodology of calculating linear regression least squares method :
least squares method : ,
,  where
where  and
and  - arithmetic mean
- arithmetic mean  and
and  .
.
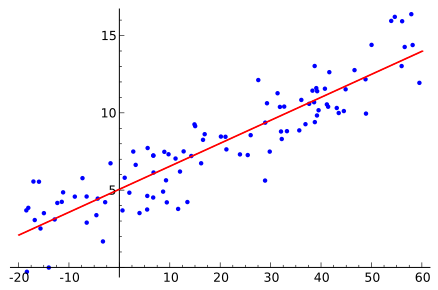
Source Wikipedia
If you use not one but several previous values, i.e. arithmetic mean of k-neighboring values, then this smoothing is called a simple moving average with a window width k
If for each previous value we use some coefficient of our own, which determines the degree of influence on the current one, then we obtain a weighted moving average .
A slightly different way is exponential smoothing. The smoothed series is calculated as follows: the first element matches the first element of the original series, but the subsequent ones are calculated by the forum
Where α is the smoothing coefficient, from 0 to 1. It is easy to see that the closer α is to 1, the more the resulting series will be similar to the original one.
To determine the linear trend, you can take the methodology of calculating linear regression

Source Wikipedia
To determine the seasonal component, we subtract the trend from the initial series or divide by it, depending on the type of the selected model, and smooth it again. Then we divide the data on the length of the season (period), usually this is a week, and we find the average season. If the length of the season is not known, then you can try to find it:
Discrete Fourier Transform or Auto Correlation
I honestly admit that I did not understand how the Fourier transform works. Those who are interested can look into the following articles: Detect Seasonality using Fourier Transform in R and Simple words about the Fourier transform . As I understand it, the original series / function is represented as an infinite sum of elements and the first few significant coefficients are taken.
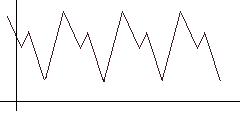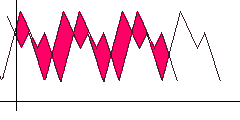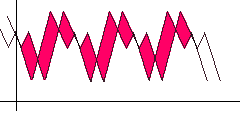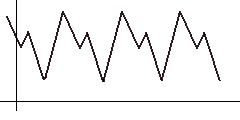
To search for auto-correlation, simply shift the function to the right and look for a position such that the distance / area between the original and shifted functions (highlighted in red) is minimal. Obviously, the shift step and the maximum limit should be set for the algorithm, upon reaching which we believe that the period search failed.

To search for auto-correlation, simply shift the function to the right and look for a position such that the distance / area between the original and shifted functions (highlighted in red) is minimal. Obviously, the shift step and the maximum limit should be set for the algorithm, upon reaching which we believe that the period search failed.
For more information on models and decompositions, see Extract Seasonal & Trend: using decomposition in R and How To Identify Patterns in Time Series Data .
Having removed the trend and the seasonal factor from the initial series, we obtain a random component.
Types of Anomalies
If we analyze only a random component, then many anomalies can be reduced to one of the following cases:
- Outlier
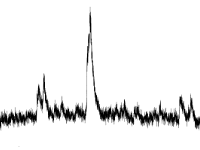 Finding outliers in data is a classic task, for the solution of which there is already a good set of solutions:The rule of three sigma, interquartile range and othersThe idea of such tests is to determine how far a single value is from the average. If the distance is different from the “normal” one, then the value is declared an outlier. The event time is ignored.
Finding outliers in data is a classic task, for the solution of which there is already a good set of solutions:The rule of three sigma, interquartile range and othersThe idea of such tests is to determine how far a single value is from the average. If the distance is different from the “normal” one, then the value is declared an outlier. The event time is ignored.
We believe that at the input a series of numbers -,
, ...
, Total
pieces.
-
th number.
Standard tests are quite simple to implement and require only the calculation of the averagestandard deviation
and sometimes medians
- the average value, if you order all the numbers in ascending order and take the one in the middle.
Rule of Three Sigma
Ifthen
consider an outlier.
Z-score and refined Iglewicz and Hoaglin method- emission if
more than a given threshold, usually equal to 3. In fact, the rewritten rule of three sigma.
The refined method is as follows: for each number in the series, we calculateand for the resulting values we find the median denoted by
.
- emission if
more threshold.
Interquartile range We
sort the initial numbers in ascending order, divide by two, and for each part we find the median valuesand
.
- emission if
.
Grubbs test
Find the minimumand maximum
values and for them we calculate
and
. Then we select the significance level α (usually one of 0.01, 0.05 or 0.1), look at the table of critical values , select a value for n and α. If
or
more than the table value, then we consider the corresponding element of the series as an outlier.
Typically, tests require that normal distribution be investigated, but often this requirement is ignored. - Shear
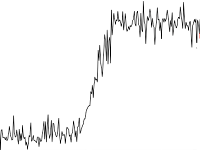 The problem of detecting a shift in data has been well studied, since it is found in signal processing. To solve it, you can use Twitter Breakout Detection . I note that it works much worse if the initial series with the components of seasonality and trend is analyzed.
The problem of detecting a shift in data has been well studied, since it is found in signal processing. To solve it, you can use Twitter Breakout Detection . I note that it works much worse if the initial series with the components of seasonality and trend is analyzed. - Changing the nature (distribution) of values
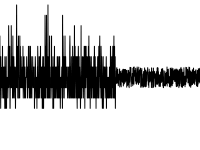 As for the shift, you can use the same BreakoutDetection package from Twitter, but not everything is smooth with it .
As for the shift, you can use the same BreakoutDetection package from Twitter, but not everything is smooth with it . - Deviation from the “everyday” (for data with seasonality)
To detect this anomaly, it is necessary to compare the current period and several previous ones. Commonly usedHolt-Winters MethodThe method relates to forecasting, therefore, its application is reduced to comparing the predicted value with the real one.
The main idea of the method is that each of the three components is exponentially smoothed using a separate smoothing coefficient, so the method is often called triple exponential smoothing. Calculation formulas for the multiplicative and addictive seasons are on Wikipedia , and details about the method are in an article on Habré .
Three smoothing parameters should be chosen so that the resulting series is "close" to the original. In practice, this task is solved by enumeration, although RRDTool requires explicitly specifying these values.
The disadvantage of the method: requires at least three seasons of data.
Another method used in Odnoklassniki is to select values from other seasons that correspond to the moment being analyzed, and check their totality for an outlier, for example, the Grubbs test.
Twitter also offers AnomalyDetection , which shows good results on test data . Unfortunately, like BreakoutDetection, it's been two years without updates. - Behavioral
Sometimes anomalies can have a specific character, which in most cases should be ignored, for example, one value in two neighboring elements. In such cases, separate algorithms are required. - Joint anomalies
Separately, it is worth mentioning the anomalies when the values of the two observed separately metrics are within normal limits, but their joint appearance is a sign of a problem. In the general case, the finding of such anomalies can be solved by cluster analysis , when pairs of values represent the coordinates of points on the plane and the whole set of events is divided into two / three groups (clusters) - “norm” / “noise” and “anomaly”.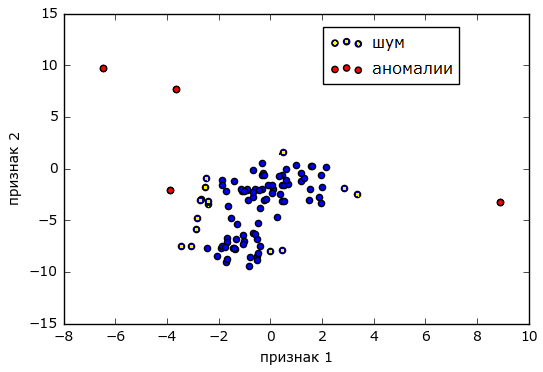
Source alexanderdyakonov.wordpress.com
A weaker method is to track how much the metrics depend on each other over time and in the case when the dependence is lost, issue an anomaly message. For this, you can probably use one of the methods.Pearson linear correlation coefficientLet beand
two sets of numbers and you need to find out if there is a linear relationship between them. We calculate for
average
and standard deviation
. Similarly for
.
Pearson correlation coefficient
The coefficient modulo closer to 1, the greater the dependence. If the coefficient is closer to -1, then the dependence is inverse, i.e. heightassociated with a decrease
.
Distance Damerau - LevenshteinLet there be two lines ABC and ADEC. To get the second from the first one, you need to remove B and add D and E. If you set a cost for each operation to delete / add a character and rearrange XY to YX, then the total cost will be the Damerau - Levenshtein distance.
To determine the similarity of the graphs, you can start with the algorithm used in KALEInitially, the initial series of values, for example, a series of the form [960, 350, 350, 432, 390, 76, 105, 715, 715], is normalized: the maximum is sought - it will correspond to 25, and the minimum - it will correspond to 0; Thus, the data is proportionally distributed in the limit of integers from 0 to 25. As a result, we get a series of the form [25, 8, 8, 10, 9, 0, 1, 18, 18]. Then the normalized series is encoded using 5 words: sdec (sharply down), dec (down), s (exactly), inc (up), sinc (sharply up). The result is a series of the form [sdec, flat, inc, dec, sdec, inc, sinc, flat].
By encoding two time series in this way, you can find out the distance between them. And if it is less than some threshold, then assume that the graphs are similar and there is a connection.
Conclusion
Of course, many algorithms for finding anomalies are already implemented in the R language , intended for statistical data processing, in the form of packages: tsoutliers , strucchange , Twitter Anomaly Detection, and others . Read more about R in articles. Do you already use R in business? and my experience of introducing R. It would seem that connect the packages and use. However, there is a problem - setting the parameters of statistical checks, which, unlike critical values, are far from obvious to most and do not have universal values. The way out of this situation may be their selection by enumeration (resource-intensive), with a rare periodic refinement, independently for each metric. On the other hand, most of the anomalies that are not related to seasonality are well defined visually, which suggests the use of a neural network for rendered graphics.
application
Below I present my own algorithms that work comparable to Twitter Breakout by results, and somewhat faster in speed when implemented in Java Script.
Piecewise linear time series approximation algorithm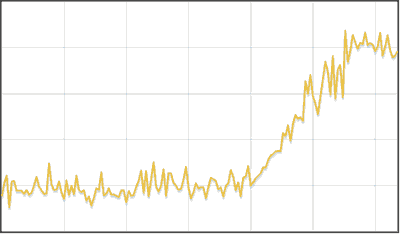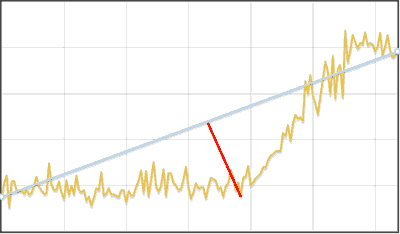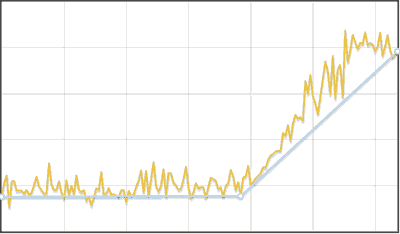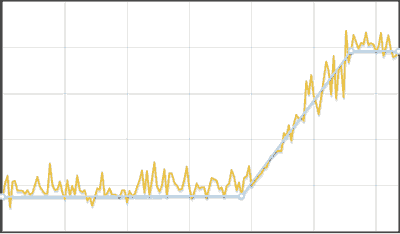

- If the row is very noisy, then we average, for example. on 5 elements.
- В результат включаем первую и последние точки ряда.
- Находим максимально удаленную точку ряда от текущей ломаной и добавляем ее в набор.
- Повторяем пока среднее отклонение от ломаной до исходного ряда не будет меньше среднего отклонения в исходном ряде или пока не достигнуто предельное число вершин ломаной (в этом случае, вероятно, апроксимация не удалась).
Алгоритм нахождения сдвига в данных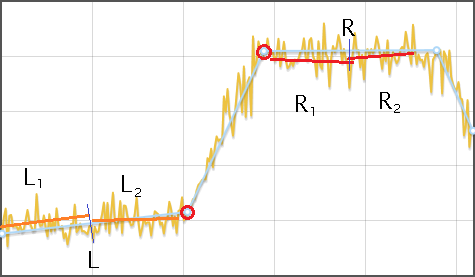

- Апроксимируем исходный ряд ломаной
- Для каждого отрезка ломаной, кроме первого и последнего:
- Находим его высоту
, как разность y-координат начала и конца. Если высота меньше игнорируемого интервала, то такой отрезок игнорируется
- Оба соседних отрезка
и
делим на двое, каждый участок
,
,
,
аппроксимируем своей прямой и находим среднее расстояние от прямой до ряда —
,
,
,
.
- Если
и
значительно меньше чем
, то считаем, что сдвиг обнаружен
- Находим его высоту
Алгоритм нахождения изменений в распределении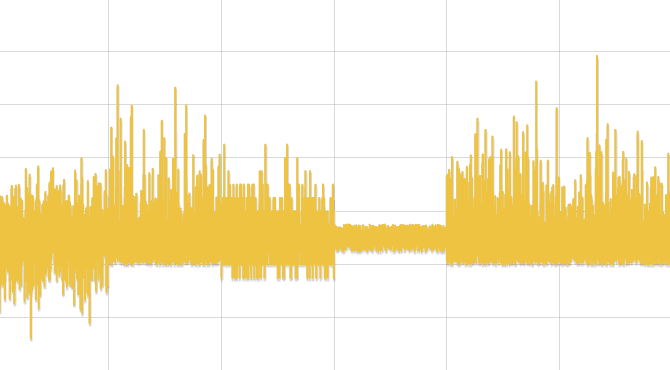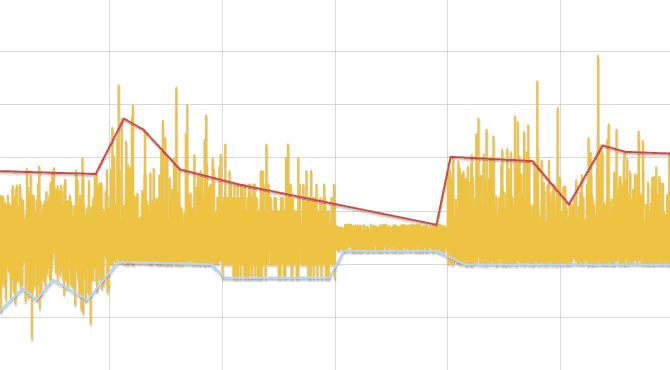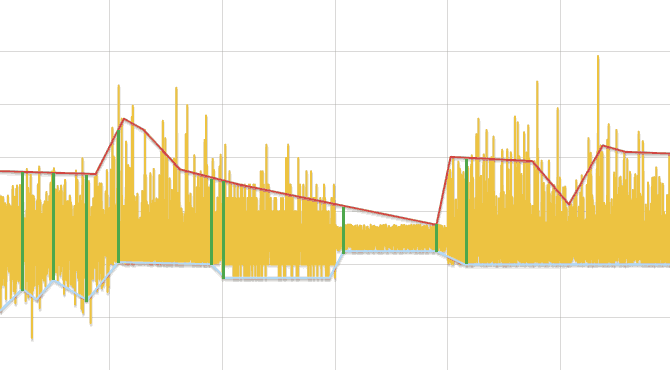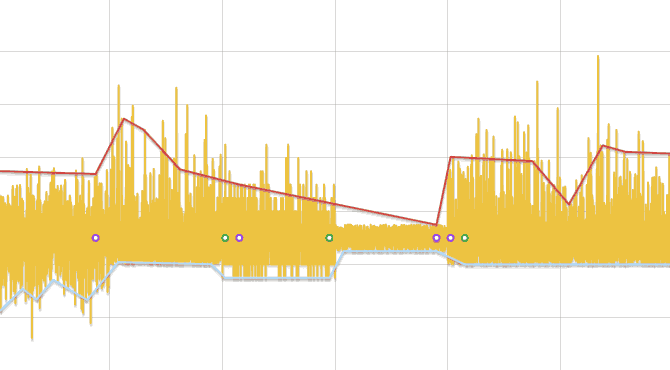

- Исходный ряд разбивается на отрезки, длинной, зависящей от числа данных, но не менее трех.
- В каждом отрезке ищется минимум и максимум. Заменяя каждый отрезок его центром, образуется два ряда — минимумы и максимумы. Далее ряды обрабатываются отдельно.
- Ряд линейно аппроксимируется и для каждой его вершины, кроме первой и последней, выполняется сравнение данных исходного ряда, лежащих слева и справа до соседних вершин ломаной, тестом Колмогорова-Смирнова. Если разница обнаружена, то точка добавляется в результат.
Тест Колмогорова-Смирнова
Пусть  и
и  два набора чисел и требуется оценить существенность различий между ними.
два набора чисел и требуется оценить существенность различий между ними.
Вначале значения обоих рядов разбиваются на несколько (около десятка) категорий. Далее для каждой категории вычисляется число , вошедших в него значений из ряда
, вошедших в него значений из ряда  , и делится на длину ряда
, и делится на длину ряда  . Аналогично для ряда
. Аналогично для ряда  . Для каждой категории находим
. Для каждой категории находим  и затем общий максимум
и затем общий максимум  по всем категориям. Проверяемое значение критерия вычисляется по формуле
по всем категориям. Проверяемое значение критерия вычисляется по формуле  .
.
Выбирается уровень значимости (один из 0.01, 0.05, 0.1) и по нему определяется критичное значение по таблице. Если
(один из 0.01, 0.05, 0.1) и по нему определяется критичное значение по таблице. Если  больше критичного значения, то считается, что группы различаются существенно.
больше критичного значения, то считается, что группы различаются существенно.
Вначале значения обоих рядов разбиваются на несколько (около десятка) категорий. Далее для каждой категории вычисляется число
Выбирается уровень значимости
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Используете ли вы автоматическое обнаружение аномалий?
- 14.2%Да10
- 74.2%Нет, но хотелось бы52
- 11.4%Нет, достаточно отслеживать критичные значения8
