We correct typographical errors in search queries.
Probably, any service that generally has a search, sooner or later comes to the need to learn how to correct errors in user requests. Errare humanum est; users are constantly sealed and mistaken, and the quality of the search inevitably suffers from this - and with it the user experience.
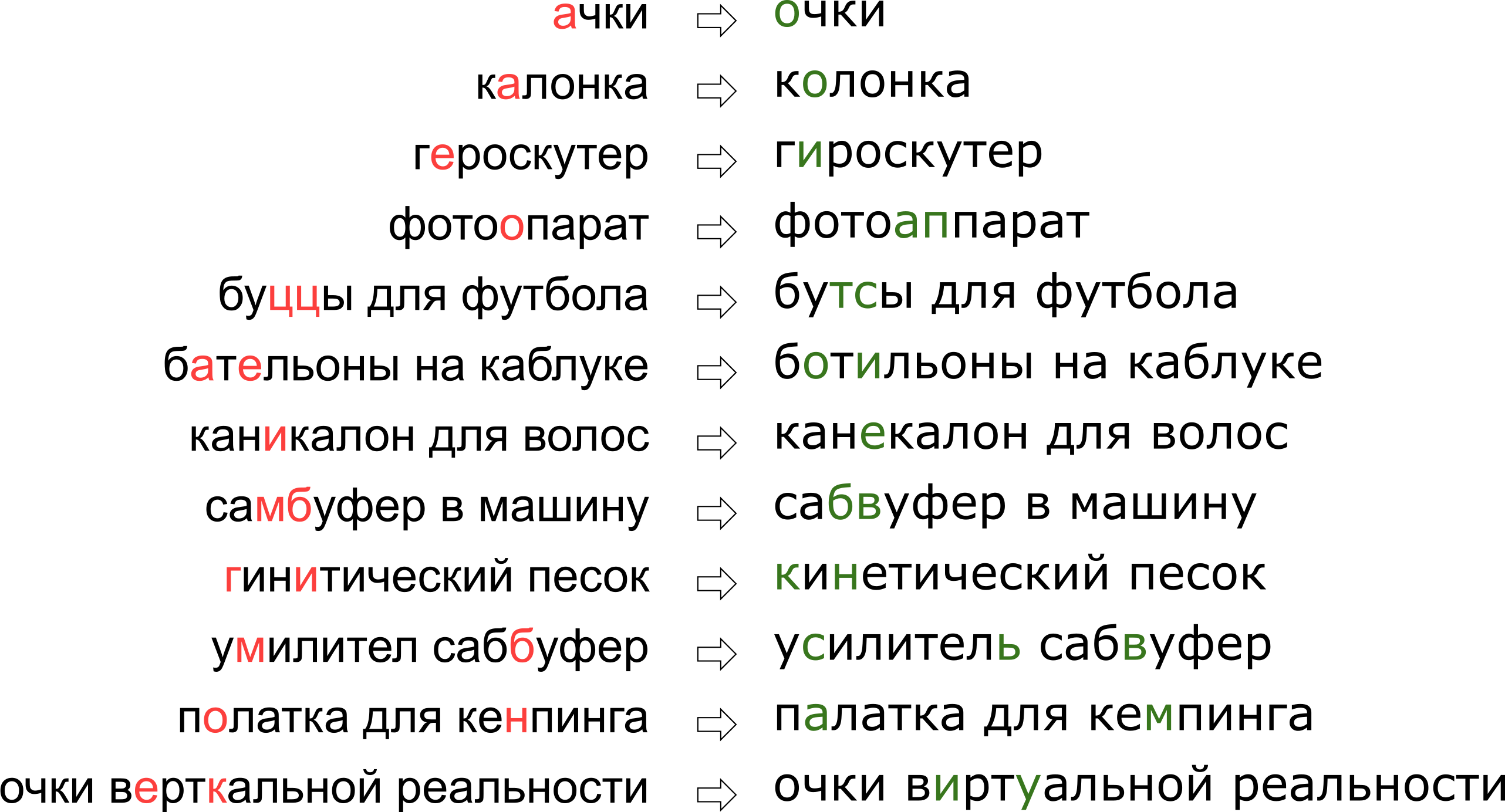
In addition, each service has its own specifics, its own lexicon, which should be able to operate on a typo fixer, which greatly complicates the use of existing solutions. For example, such requests had to learn to correct our guardian: It may seem that we denied the user his dream of vertical reality, but in fact the letter K just stands on the keyboard next to the letter U.
In this article we will analyze one of the classic approaches to correcting typos, from building a model to writing code in Python and Go. And as a bonus - a video from my report “ “ Glasses of the Vertical Reality ”: correcting typos in search queries ” on Highload ++.
So, we received a sealed request and it needs to be fixed. Usually the problem is mathematically set as follows:
This formulation - the most elementary - assumes that if we received a request from several words, then we correct each word separately. In reality, of course, we will want to correct the entire phrase, taking into account the compatibility of neighboring words; I will tell about it below, in the section “How to correct phrases”.
There are two unclear moments - where to get the dictionary and how to count. The first question is considered simple. In 1990, [1] the dictionary was collected from the spell utility database and dictionaries available in electronic form; in 2009, Google [4] made it easier and simply took the top most popular words on the Internet (along with the popular erroneous spellings). I also took this approach to build my girdle.
The second question is more complicated. If only because his decision usually begins with the application of the Bayes formula!
Now, instead of the original incomprehensible probability, we need to evaluate two new, slightly more understandable ones: - the probability that when typing a word can be sealed and get and - in principle, the probability of the user using the word .
How to evaluate? Obviously, the user is more likely to confuse A with O than b with B. And if we correct the text recognized from the scanned document, then there is a high probability of confusion between rn and m. Anyway, we need some kind of model that describes errors and their probabilities.
Such a model is called the noisy channel model (the model of a noisy channel; in our case, a noisy channel starts somewhere in the center of the user's Brok and ends on the other side of its keyboard) or, more briefly, the error model is an error model. This model, to which a separate section is devoted below, will be responsible for recording both spelling errors and, in fact, typos.
Rate the likelihood of using the word -- can be different. The easiest option is to take for it the frequency with which the word occurs in some large corpus of texts. For our girder, taking into account the context of the phrase, we will need, of course, something more complicated - another model. This model is called a language model, a language model.
The first error models considered , counting the probabilities of elementary substitutions in the training sample: how many times E was written instead of E, T was written instead of T, T was written instead of T, and so on [1]. A model with a small number of parameters was obtained, capable of learning some local effects (for example, that people often confuse E and I).
In our research, we dwelt on a more advanced model of errors proposed in 2000 by Brill and Moore [2] and reused later (for example, by Google [4]). Imagine that users do not think in separate characters (confuse E and I, press K instead of U, skip a soft sign), but can change arbitrary pieces of a word to any others - for example, replace TCA with TSS, U with K, SCHA on OA, SS on C and so on. The probability that a user has been sealed and instead of TCJA has written by THS, we denote- this is the parameter of our model. If for all possible fragments we can count , then the desired probability typing the word s when trying to type the word w in the Brill and Moore model can be obtained as follows: we divide the words w and s into shorter fragments in all possible ways so that the fragments in two words have the same number. For each partition we calculate the product of the probabilities of all fragments w to turn into the corresponding fragments s. Maximum for all such partitions and take for the value of:
Let's look at an example of the partitioning that occurs when calculating the probability of typing “accessory” instead of “accessory”:
As you probably noticed, this is an example of a not very successful partition: it is clear that parts of the words did not lie under each other as well as they could. If values and still not so bad then and , most likely, they will make the final “score” of this partition absolutely sad. A better partitioning looks something like this:
Here everything immediately fell into place, and it is clear that the final probability will be determined mainly by the value .
Despite the fact that the possible splits for two words are of the order using dynamic programming calculation algorithm can be done quite quickly - for . The algorithm itself will very strongly resemble the Wagner-Fisher algorithm for calculating the Levenshtein distance .
We will create a rectangular table, the rows of which will correspond to the letters of the correct word, and the columns - sealed. In the cell at the intersection of row i and column j, by the end of the algorithm will lie exactly the probability of getting
, then to fill the cell in the fourth row and the third column (gray) you need to take the maximum of the values and . At the same time, we ran through all the cells highlighted in green in the image. If we also consider modifications of the form and , it is necessary to run through the cells highlighted in yellow.
The complexity of this algorithm, as I mentioned above, is: we fill the table , and to fill the cell (i, j) you need operations. However, if we limit consideration to fragments no more than some limited length (for example, no more than two letters, as in [4]), the complexity decreases to . For the Russian language in my experiments, I took.
We learned to find in polynomial time is good. But we need to learn to quickly find the best words in the whole dictionary. And the best are notand by ! In fact, we only need to get some reasonable top (for example, the top 20) bywhich we will then send to the language model to select the most appropriate fixes (more on this below).
To learn how to quickly go through the entire dictionary, we note that the table presented above will have much in common for two words with common prefixes. Indeed, if we, correcting the word “accessory”, try to fill it in for two vocabulary words “accessory” and “accessories”, we notice that the first nine lines in them do not differ at all! If we can organize the passage through the dictionary in such a way that the two subsequent words have rather long common prefixes, we can save a lot of calculations.
And we can. Let's take vocabulary words and make trie of them. Going through it by searching in depth, we get the desired property: most of the steps are steps from the node to its descendant, when the table has enough to fill in the last few lines.
This algorithm, with some additional optimizations, allows us to iterate through the dictionary of a typical European language in 50-100 thousand words within a hundred milliseconds [2]. And caching the results will make the process even faster.
Calculation for all the considered fragments - the most interesting and nontrivial part of the construction of the error model. It is from these values that its quality will depend.
The approach used in [2, 4] is relatively simple. Let's find a lot of pairswhere - the correct word from the dictionary, and - its sealed version. (How exactly to find them - just below.) Now we need to extract specific misprints from these pairs of probabilities (replacing some fragments with others).
For each pair we take its components and and construct a correspondence between their letters, minimizing the Levenshtein distance:
Now we immediately see the replacements: a → a, e → and, c → c, c → empty line, and so on. We also see the replacement of two or more characters: ak → ak, ce → si, eu → iz, ss → s, si → sis, ess → is and so on and so forth. All these replacements must be counted, and each as many times as the word s occurs in the body (if we took words from the body, which is very likely).
After going through all the pairs for probability The number of substitutions α → β occurring in our pairs (taking into account the occurrence of the corresponding words), divided by the number of repetitions of the α fragment, is taken.
How to find pairs? In [4], this approach is proposed. Take the large corpus of user-generated content (UGC). In the case of Google, these were simply the texts of hundreds of millions of web pages; in our - millions of user searches and reviews. It is assumed that the correct word is usually found in the corpus more often than any of the erroneous variants. So, let's find for each word words from the hull that are close to him according to Lowenstein, which are much less popular (for example, ten times). Popular take forless popular for . So we get even noisy, but a fairly large set of pairs, on which it will be possible to conduct training.
This matching algorithm leaves plenty of room for improvement. In [4], only a filter by frequency is proposed ( ten times more popular than ), but the authors of this article are trying to do the gadget without using any a priori knowledge of the language. If we consider only the Russian language, we can, for example, take a set of dictionaries of Russian word forms and leave only pairs with the wordfound in the dictionary (not the best idea, because the dictionary will most likely not be specific to the vocabulary service) or, on the contrary, discard pairs with the word s found in the dictionary (that is, almost guaranteed not to be sealed).
To improve the quality of the resulting pairs, I wrote a simple function that determines whether users use two words as synonyms. The logic is simple: if the words w and s are often found in the environment of the same words, then they are probably synonymous - which, in the light of their proximity to Levenshtey, means that a less popular word is most likely an erroneous version of a more popular one. For these calculations, I used the statistics for the occurrence of trigrams (three-word phrases) constructed for the language model.
So now for the given vocabulary word w we need to calculate - the probability of its use by the user. The simplest solution is to take the occurrence of a word in some large package. In general, probably, any language model begins with collecting a large body of texts and counting the occurrence of words in it. But we should not limit ourselves to this: in fact, when calculating P (w), we can also take into account the phrase, the word in which we are trying to correct, and any other external context. The task turns into the task of computingwhere one of - the word in which we corrected a typo and for which we now count and the rest - the words surrounding the corrected word in the user query.
To learn how to take them into account, it is worth walking around the body again and compiling statistics for n-grams, sequences of words. Usually take sequences of limited length; I limited myself to trigrams, so as not to inflate the index, but it all depends on your strength of mind (and the size of the body - on a small case, even statistics on trigrams will be too noisy).
The traditional language model based on n-grams looks like this. For the phrase its probability is calculated by the formula
Where - directly the frequency of the word, and - word probability under the condition that before him go - Nothing but the ratio of the frequency of the trigram to bigram frequency . (Note that this formula is simply the result of repeatedly applying the Bayes formula.)
In other words, if we want to calculatedenoting the frequency of an arbitrary n-gram for we get the formula
Is it logical Is logical. However, difficulties begin when phrases become longer. What if the user typed in an impressively detailed search query in ten words? We do not want to keep statistics on all 10 grams - this is expensive, and the data will most likely be noisy and not indicative. We want to do with n-grams of some limited length — for example, the length 3 already proposed above.
This is where the formula above comes in handy. Let's assume that the probability of a word appearing at the end of a phrase is significantly affected by only a few words immediately before it, that is, that
Putting down , for a longer phrase, we get the formula
Please note: the phrase consists of five words, but n-grams no longer than three appear in the formula. This is exactly what we wanted.
Only one subtle moment remained. What if the user entered a very strange phrase and the corresponding n-grams in our statistics and not at all? It would be easy for unfamiliar n-grams to putif it were not necessary to divide this value. Here smoothing comes to the rescue, which can be done in various ways; However, a detailed discussion of serious smoothing approaches like Kneser-Ney smoothing goes far beyond the scope of this article.
Let's discuss the last subtle point before proceeding to the implementation. The statement of the problem I described above implied that there is one word and it needs to be corrected. Then we clarified that this one word may be in the middle of a phrase among some other words and they also need to be taken into account when choosing the best correction. But in reality, users simply send us phrases without specifying which word is written with an error; often a few words need to be corrected or even all.
There can be many approaches here. You can, for example, take into account only the left context of the word in the phrase. Then, walking along the words from left to right and correcting them as necessary, we will get a new phrase of some quality. The quality will be low if, for example, the first word turned out to be similar to several popular words and we choose the wrong option. The rest of the phrase (perhaps, initially unmistakable in general) will be adjusted by us to the wrong first word and we can get the text completely irrelevant to the original.
You can consider the words separately and use a classifier to understand whether this word is sealed or not, as proposed in [4]. The classifier is trained on probabilities, which we can already count, and a number of other features. If the classifier says that it is necessary to correct - we correct it, taking into account the existing context. Again, if several words are written with an error, it is necessary to make a decision about the first of them, relying on the context with errors, which can lead to quality problems.
In the implementation of our girdle, we used this approach. Let's go for each word in our phrase, we will find, using the error model, top-N dictionary words that could be in mind, we concatenate them into phrases in various ways and for each of the resulting phrases where - the number of words in the source phrase, we honestly calculate the value
Here - words entered by the user - corrections selected for them (which we are going through now), and - the coefficient determined by the comparative quality of the error model and the language model (a large coefficient — we trust the language model more; a small coefficient — we trust the error model more) proposed in [4]. Total for each phrase, we multiply the probabilities of individual words to correct in the corresponding vocabulary variants and multiply this by the probability of the entire phrase in our language. The result of the algorithm is a phrase from vocabulary words that maximizes this value.
So, stop, what? Bustphrases?
Fortunately, due to the fact that we have limited the length of n-grams, it is possible to find the maximum for all the phrases much faster. Remember: above, we have simplified the formula for so that it became dependent only on frequencies n-grams of length not higher than three:
If we multiply this value by and try to maximize by , we will see that it is enough to sort out all kinds of and and solve the problem for them - that is, for phrases . Total problem is solved by dynamic programming for.
Immediately make a reservation: the data at my disposal was not so much to get some kind of complex MapReduce. So I just collected all the texts of reviews, comments and search queries in Russian (descriptions of products, alas, come in English, and using the results of the autotranslation worsened rather than improved the results) from our service into one text file and set the server to read at night trigrams in a simple Python script.
As vocabulary, I took the top words in frequency so that I got about a hundred thousand words. Too long words (more than 20 characters) and too short (less than three characters, except for the well-known Russian words) were excluded. Separately, he spared the words on a regular basis
When calculating bigrams and trigrams in a phrase, a non-vocabulary word may occur. In this case, I threw out this word and beat the entire phrase into two parts (before and after this word), with which I worked separately. So, for the phrase " Do you know what abyrvalg is?" This ... HEADS, colleague "will take into account the trigrams" and you know "," you know what "," know what "and" this is the head fish colleague "(if, of course, the word" head fish "falls into the dictionary ...).
Further I carried out all data processing in Jupyter. Statistics on n-grams is loaded from JSON, post-processing is performed in order to quickly find words that are close to each other according to Levenshteyn, and for pairs in a cycle, a (rather cumbersome) function is called that builds words and extracts short edits like ss → s (under the spoiler).
The very counting of edits looks elementary, although it can take a long time.
This part is implemented as a Go microservice associated with the main backend via gRPC. The algorithm described by Brill and Moore [2] was implemented, with small optimizations. It works for me in the end, about twice as slowly as the authors claimed; I do not presume to judge whether the matter is in Go or in me. But in the course of profiling, I learned a little about Go.
Here, without special surprises, the dynamic programming algorithm described in the section above was implemented. This component had the least work — the slowest part is the use of the error model. Therefore, between these two layers, the caching of the error model results in Redis was additionally screwed.
According to the results of this work (which occupied about a month), we performed an A / B test of a guard on our users. Instead of 10% of empty returns among all the search queries that we had before the introduction of the guard, they became 5%; Most of the remaining requests are for goods that we simply do not have on the platform. Also increased the number of sessions without a second search query (and a few more metrics of this kind related to UX). The metrics associated with money, however, did not significantly change - it was unexpected and encouraged us to carefully analyze and re-check other metrics.
Stephen Hawking was once told that every formula he included in the book would halve the number of readers. Well, in this article, their order is fifty - congratulations, one of about readers who have reached this place!
[1] MD Kernighan, KW Church, WA Gale. A Spelling Correction Program Based on a Noisy Channel Model . Proceedings of the 13th Conference on Computational Linguistics - Volume 2, 1990.
[2] E.Brill, RC Moore. An Improved Error Code for Noisy Channel Spelling Correction . Proceedings of the 38th Annual Meeting on Computational Linguistics, 2000.
[3] T. Brants, AC Popat, P. Xu, FJ Och, J. Dean. Large Language Models in Machine Translation . Proceedings of the 2007 Conference on Empirical Methods in Natural Language Processing.
[4] C. Whitelaw, B. Hutchinson, GY Chung, G. Ellis. Using the Web for Language Independent Spellchecking and Autocorrection. Proceedings of the 2009 Conference on Empirical Methods of Natural Language Processing: Volume 2.
In addition, each service has its own specifics, its own lexicon, which should be able to operate on a typo fixer, which greatly complicates the use of existing solutions. For example, such requests had to learn to correct our guardian: It may seem that we denied the user his dream of vertical reality, but in fact the letter K just stands on the keyboard next to the letter U.

In this article we will analyze one of the classic approaches to correcting typos, from building a model to writing code in Python and Go. And as a bonus - a video from my report “ “ Glasses of the Vertical Reality ”: correcting typos in search queries ” on Highload ++.
Formulation of the problem
So, we received a sealed request and it needs to be fixed. Usually the problem is mathematically set as follows:
- given word passed to us with errors;
- have a dictionary correct words;
- for all words w in the dictionary there are conditional probabilities what the word meant , provided that we have received the word ;
- need to find the word w from the dictionary with the maximum probability .
This formulation - the most elementary - assumes that if we received a request from several words, then we correct each word separately. In reality, of course, we will want to correct the entire phrase, taking into account the compatibility of neighboring words; I will tell about it below, in the section “How to correct phrases”.
There are two unclear moments - where to get the dictionary and how to count. The first question is considered simple. In 1990, [1] the dictionary was collected from the spell utility database and dictionaries available in electronic form; in 2009, Google [4] made it easier and simply took the top most popular words on the Internet (along with the popular erroneous spellings). I also took this approach to build my girdle.
The second question is more complicated. If only because his decision usually begins with the application of the Bayes formula!
Now, instead of the original incomprehensible probability, we need to evaluate two new, slightly more understandable ones: - the probability that when typing a word can be sealed and get and - in principle, the probability of the user using the word .
How to evaluate? Obviously, the user is more likely to confuse A with O than b with B. And if we correct the text recognized from the scanned document, then there is a high probability of confusion between rn and m. Anyway, we need some kind of model that describes errors and their probabilities.
Such a model is called the noisy channel model (the model of a noisy channel; in our case, a noisy channel starts somewhere in the center of the user's Brok and ends on the other side of its keyboard) or, more briefly, the error model is an error model. This model, to which a separate section is devoted below, will be responsible for recording both spelling errors and, in fact, typos.
Rate the likelihood of using the word -- can be different. The easiest option is to take for it the frequency with which the word occurs in some large corpus of texts. For our girder, taking into account the context of the phrase, we will need, of course, something more complicated - another model. This model is called a language model, a language model.
Error model
The first error models considered , counting the probabilities of elementary substitutions in the training sample: how many times E was written instead of E, T was written instead of T, T was written instead of T, and so on [1]. A model with a small number of parameters was obtained, capable of learning some local effects (for example, that people often confuse E and I).
In our research, we dwelt on a more advanced model of errors proposed in 2000 by Brill and Moore [2] and reused later (for example, by Google [4]). Imagine that users do not think in separate characters (confuse E and I, press K instead of U, skip a soft sign), but can change arbitrary pieces of a word to any others - for example, replace TCA with TSS, U with K, SCHA on OA, SS on C and so on. The probability that a user has been sealed and instead of TCJA has written by THS, we denote- this is the parameter of our model. If for all possible fragments we can count , then the desired probability typing the word s when trying to type the word w in the Brill and Moore model can be obtained as follows: we divide the words w and s into shorter fragments in all possible ways so that the fragments in two words have the same number. For each partition we calculate the product of the probabilities of all fragments w to turn into the corresponding fragments s. Maximum for all such partitions and take for the value of:
Let's look at an example of the partitioning that occurs when calculating the probability of typing “accessory” instead of “accessory”:
As you probably noticed, this is an example of a not very successful partition: it is clear that parts of the words did not lie under each other as well as they could. If values and still not so bad then and , most likely, they will make the final “score” of this partition absolutely sad. A better partitioning looks something like this:
Here everything immediately fell into place, and it is clear that the final probability will be determined mainly by the value .
How to calculate
Despite the fact that the possible splits for two words are of the order using dynamic programming calculation algorithm can be done quite quickly - for . The algorithm itself will very strongly resemble the Wagner-Fisher algorithm for calculating the Levenshtein distance .
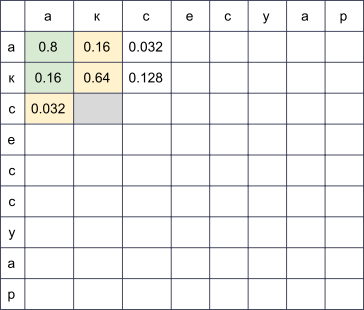
We will create a rectangular table, the rows of which will correspond to the letters of the correct word, and the columns - sealed. In the cell at the intersection of row i and column j, by the end of the algorithm will lie exactly the probability of getting
s[:j]when trying to print w[:i]. In order to calculate it, it is sufficient to calculate the values of all cells in the previous rows and columns and run through them, multiplying by the corresponding. For example, if we have a table
, then to fill the cell in the fourth row and the third column (gray) you need to take the maximum of the values and . At the same time, we ran through all the cells highlighted in green in the image. If we also consider modifications of the form and , it is necessary to run through the cells highlighted in yellow.
The complexity of this algorithm, as I mentioned above, is: we fill the table , and to fill the cell (i, j) you need operations. However, if we limit consideration to fragments no more than some limited length (for example, no more than two letters, as in [4]), the complexity decreases to . For the Russian language in my experiments, I took.
How to maximize
We learned to find in polynomial time is good. But we need to learn to quickly find the best words in the whole dictionary. And the best are notand by ! In fact, we only need to get some reasonable top (for example, the top 20) bywhich we will then send to the language model to select the most appropriate fixes (more on this below).
To learn how to quickly go through the entire dictionary, we note that the table presented above will have much in common for two words with common prefixes. Indeed, if we, correcting the word “accessory”, try to fill it in for two vocabulary words “accessory” and “accessories”, we notice that the first nine lines in them do not differ at all! If we can organize the passage through the dictionary in such a way that the two subsequent words have rather long common prefixes, we can save a lot of calculations.
And we can. Let's take vocabulary words and make trie of them. Going through it by searching in depth, we get the desired property: most of the steps are steps from the node to its descendant, when the table has enough to fill in the last few lines.
This algorithm, with some additional optimizations, allows us to iterate through the dictionary of a typical European language in 50-100 thousand words within a hundred milliseconds [2]. And caching the results will make the process even faster.
How to get
Calculation for all the considered fragments - the most interesting and nontrivial part of the construction of the error model. It is from these values that its quality will depend.
The approach used in [2, 4] is relatively simple. Let's find a lot of pairswhere - the correct word from the dictionary, and - its sealed version. (How exactly to find them - just below.) Now we need to extract specific misprints from these pairs of probabilities (replacing some fragments with others).
For each pair we take its components and and construct a correspondence between their letters, minimizing the Levenshtein distance:
Now we immediately see the replacements: a → a, e → and, c → c, c → empty line, and so on. We also see the replacement of two or more characters: ak → ak, ce → si, eu → iz, ss → s, si → sis, ess → is and so on and so forth. All these replacements must be counted, and each as many times as the word s occurs in the body (if we took words from the body, which is very likely).
After going through all the pairs for probability The number of substitutions α → β occurring in our pairs (taking into account the occurrence of the corresponding words), divided by the number of repetitions of the α fragment, is taken.
How to find pairs? In [4], this approach is proposed. Take the large corpus of user-generated content (UGC). In the case of Google, these were simply the texts of hundreds of millions of web pages; in our - millions of user searches and reviews. It is assumed that the correct word is usually found in the corpus more often than any of the erroneous variants. So, let's find for each word words from the hull that are close to him according to Lowenstein, which are much less popular (for example, ten times). Popular take forless popular for . So we get even noisy, but a fairly large set of pairs, on which it will be possible to conduct training.
This matching algorithm leaves plenty of room for improvement. In [4], only a filter by frequency is proposed ( ten times more popular than ), but the authors of this article are trying to do the gadget without using any a priori knowledge of the language. If we consider only the Russian language, we can, for example, take a set of dictionaries of Russian word forms and leave only pairs with the wordfound in the dictionary (not the best idea, because the dictionary will most likely not be specific to the vocabulary service) or, on the contrary, discard pairs with the word s found in the dictionary (that is, almost guaranteed not to be sealed).
To improve the quality of the resulting pairs, I wrote a simple function that determines whether users use two words as synonyms. The logic is simple: if the words w and s are often found in the environment of the same words, then they are probably synonymous - which, in the light of their proximity to Levenshtey, means that a less popular word is most likely an erroneous version of a more popular one. For these calculations, I used the statistics for the occurrence of trigrams (three-word phrases) constructed for the language model.
Language model
So now for the given vocabulary word w we need to calculate - the probability of its use by the user. The simplest solution is to take the occurrence of a word in some large package. In general, probably, any language model begins with collecting a large body of texts and counting the occurrence of words in it. But we should not limit ourselves to this: in fact, when calculating P (w), we can also take into account the phrase, the word in which we are trying to correct, and any other external context. The task turns into the task of computingwhere one of - the word in which we corrected a typo and for which we now count and the rest - the words surrounding the corrected word in the user query.
To learn how to take them into account, it is worth walking around the body again and compiling statistics for n-grams, sequences of words. Usually take sequences of limited length; I limited myself to trigrams, so as not to inflate the index, but it all depends on your strength of mind (and the size of the body - on a small case, even statistics on trigrams will be too noisy).
The traditional language model based on n-grams looks like this. For the phrase its probability is calculated by the formula
Where - directly the frequency of the word, and - word probability under the condition that before him go - Nothing but the ratio of the frequency of the trigram to bigram frequency . (Note that this formula is simply the result of repeatedly applying the Bayes formula.)
In other words, if we want to calculatedenoting the frequency of an arbitrary n-gram for we get the formula
Is it logical Is logical. However, difficulties begin when phrases become longer. What if the user typed in an impressively detailed search query in ten words? We do not want to keep statistics on all 10 grams - this is expensive, and the data will most likely be noisy and not indicative. We want to do with n-grams of some limited length — for example, the length 3 already proposed above.
This is where the formula above comes in handy. Let's assume that the probability of a word appearing at the end of a phrase is significantly affected by only a few words immediately before it, that is, that
Putting down , for a longer phrase, we get the formula
Please note: the phrase consists of five words, but n-grams no longer than three appear in the formula. This is exactly what we wanted.
Only one subtle moment remained. What if the user entered a very strange phrase and the corresponding n-grams in our statistics and not at all? It would be easy for unfamiliar n-grams to putif it were not necessary to divide this value. Here smoothing comes to the rescue, which can be done in various ways; However, a detailed discussion of serious smoothing approaches like Kneser-Ney smoothing goes far beyond the scope of this article.
How to correct phrases
Let's discuss the last subtle point before proceeding to the implementation. The statement of the problem I described above implied that there is one word and it needs to be corrected. Then we clarified that this one word may be in the middle of a phrase among some other words and they also need to be taken into account when choosing the best correction. But in reality, users simply send us phrases without specifying which word is written with an error; often a few words need to be corrected or even all.
There can be many approaches here. You can, for example, take into account only the left context of the word in the phrase. Then, walking along the words from left to right and correcting them as necessary, we will get a new phrase of some quality. The quality will be low if, for example, the first word turned out to be similar to several popular words and we choose the wrong option. The rest of the phrase (perhaps, initially unmistakable in general) will be adjusted by us to the wrong first word and we can get the text completely irrelevant to the original.
You can consider the words separately and use a classifier to understand whether this word is sealed or not, as proposed in [4]. The classifier is trained on probabilities, which we can already count, and a number of other features. If the classifier says that it is necessary to correct - we correct it, taking into account the existing context. Again, if several words are written with an error, it is necessary to make a decision about the first of them, relying on the context with errors, which can lead to quality problems.
In the implementation of our girdle, we used this approach. Let's go for each word in our phrase, we will find, using the error model, top-N dictionary words that could be in mind, we concatenate them into phrases in various ways and for each of the resulting phrases where - the number of words in the source phrase, we honestly calculate the value
Here - words entered by the user - corrections selected for them (which we are going through now), and - the coefficient determined by the comparative quality of the error model and the language model (a large coefficient — we trust the language model more; a small coefficient — we trust the error model more) proposed in [4]. Total for each phrase, we multiply the probabilities of individual words to correct in the corresponding vocabulary variants and multiply this by the probability of the entire phrase in our language. The result of the algorithm is a phrase from vocabulary words that maximizes this value.
So, stop, what? Bustphrases?
Fortunately, due to the fact that we have limited the length of n-grams, it is possible to find the maximum for all the phrases much faster. Remember: above, we have simplified the formula for so that it became dependent only on frequencies n-grams of length not higher than three:
If we multiply this value by and try to maximize by , we will see that it is enough to sort out all kinds of and and solve the problem for them - that is, for phrases . Total problem is solved by dynamic programming for.
Implementation
Putting the body and count n-grams
Immediately make a reservation: the data at my disposal was not so much to get some kind of complex MapReduce. So I just collected all the texts of reviews, comments and search queries in Russian (descriptions of products, alas, come in English, and using the results of the autotranslation worsened rather than improved the results) from our service into one text file and set the server to read at night trigrams in a simple Python script.
As vocabulary, I took the top words in frequency so that I got about a hundred thousand words. Too long words (more than 20 characters) and too short (less than three characters, except for the well-known Russian words) were excluded. Separately, he spared the words on a regular basis
r"^[a-z0-9]{2}$" - so that versions of iPhones and other interesting identifiers of length 2 would survive.When calculating bigrams and trigrams in a phrase, a non-vocabulary word may occur. In this case, I threw out this word and beat the entire phrase into two parts (before and after this word), with which I worked separately. So, for the phrase " Do you know what abyrvalg is?" This ... HEADS, colleague "will take into account the trigrams" and you know "," you know what "," know what "and" this is the head fish colleague "(if, of course, the word" head fish "falls into the dictionary ...).
We teach the error model
Further I carried out all data processing in Jupyter. Statistics on n-grams is loaded from JSON, post-processing is performed in order to quickly find words that are close to each other according to Levenshteyn, and for pairs in a cycle, a (rather cumbersome) function is called that builds words and extracts short edits like ss → s (under the spoiler).
Python code
defgenerate_modifications(intended_word, misspelled_word, max_l=2):# Выстраиваем буквы слов оптимальным по Левенштейну образом и# извлекаем модификации ограниченной длины. Чтобы после подсчёта# расстояния восстановить оптимальное расположение букв, будем# хранить в таблице помимо расстояний указатели на предыдущие# ячейки: memo будет хранить соответствие# i -> j -> (distance, prev i, prev j).# Дальше немного непривычно страшного Python кода - вот что# бывает, когда язык используется не по назначению!
m, n = len(intended_word), len(misspelled_word)
memo = [[None] * (n+1) for _ in range(m+1)]
memo[0] = [(j, (0if j > 0else-1), j-1) for j in range(n+1)]
for i in range(m + 1):
memo[i][0] = i, i-1, (0if i > 0else-1)
for j in range(1, n + 1):
for i in range(1, m + 1):
if intended_word[i-1] == misspelled_word[j-1]:
memo[i][j] = memo[i-1][j-1][0], i-1, j-1else:
best = min(
(memo[i-1][j][0], i-1, j),
(memo[i][j-1][0], i, j-1),
(memo[i-1][j-1][0], i-1, j-1),
)
# Отдельная обработка для перепутанных местами# соседних букв (распространённая ошибка при# печати).if (i > 1and j > 1and intended_word[i-1] == misspelled_word[j-2]
and intended_word[i-2] == misspelled_word[j-1]
):
best = min(best, (memo[i-2][j-2][0], i-2, j-2))
memo[i][j] = 1 + best[0], best[1], best[2]
# К концу цикла расстояние по Левенштейну между исходными словами # хранится в memo[m][n][0]. # Теперь восстанавливаем оптимальное расположение букв.
s, t = [], []
i, j = m, n
while i >= 1or j >= 1:
_, pi, pj = memo[i][j]
di, dj = i - pi, j - pj
if di == dj == 1:
s.append(intended_word[i-1])
t.append(misspelled_word[j-1])
if di == dj == 2:
s.append(intended_word[i-1])
s.append(intended_word[i-2])
t.append(misspelled_word[j-1])
t.append(misspelled_word[j-2])
if1 == di > dj == 0:
s.append(intended_word[i-1])
t.append("")
if1 == dj > di == 0:
s.append("")
t.append(misspelled_word[j-1])
i, j = pi, pj
s.reverse()
t.reverse()
# Генерируем модификации длины не выше заданной.for i, _ in enumerate(s):
ss = ts = ""while len(ss) < max_l and i < len(s):
ss += s[i]
ts += t[i]
yield ss, ts
i += 1The very counting of edits looks elementary, although it can take a long time.
We apply error model
This part is implemented as a Go microservice associated with the main backend via gRPC. The algorithm described by Brill and Moore [2] was implemented, with small optimizations. It works for me in the end, about twice as slowly as the authors claimed; I do not presume to judge whether the matter is in Go or in me. But in the course of profiling, I learned a little about Go.
- Do not use
math.Maxto count the maximum. This is about three times slower thanif a > b { b = a }! Just look at the implementation of this feature :// Max returns the larger of x or y.//// Special cases are:// Max(x, +Inf) = Max(+Inf, x) = +Inf// Max(x, NaN) = Max(NaN, x) = NaN// Max(+0, ±0) = Max(±0, +0) = +0// Max(-0, -0) = -0funcMax(x, y float64)float64funcmax(x, y float64)float64 { // special casesswitch { case IsInf(x, 1) || IsInf(y, 1): return Inf(1) case IsNaN(x) || IsNaN(y): return NaN() case x == 0 && x == y: if Signbit(x) { return y } return x } if x > y { return x } return y }
Unless you suddenly need to, that +0 must be more than -0, do not usemath.Max. - Do not use a hash table if you can use an array. This, of course, is pretty obvious advice. I had to renumber the unicode characters at the beginning of the program so that they could be used as indices in the array of descendants of the trie node (such a lookup was a very frequent operation).
- Callbacks in Go are not cheap. During the refactoring during the code review, some of my attempts to do decoupling significantly slowed down the program, although the algorithm did not formally change. Since then I have been left with the opinion that the Go optimizer compiler has where to grow.
Apply the language model
Here, without special surprises, the dynamic programming algorithm described in the section above was implemented. This component had the least work — the slowest part is the use of the error model. Therefore, between these two layers, the caching of the error model results in Redis was additionally screwed.
results
According to the results of this work (which occupied about a month), we performed an A / B test of a guard on our users. Instead of 10% of empty returns among all the search queries that we had before the introduction of the guard, they became 5%; Most of the remaining requests are for goods that we simply do not have on the platform. Also increased the number of sessions without a second search query (and a few more metrics of this kind related to UX). The metrics associated with money, however, did not significantly change - it was unexpected and encouraged us to carefully analyze and re-check other metrics.
Conclusion
Stephen Hawking was once told that every formula he included in the book would halve the number of readers. Well, in this article, their order is fifty - congratulations, one of about readers who have reached this place!
Bonus
Links
[1] MD Kernighan, KW Church, WA Gale. A Spelling Correction Program Based on a Noisy Channel Model . Proceedings of the 13th Conference on Computational Linguistics - Volume 2, 1990.
[2] E.Brill, RC Moore. An Improved Error Code for Noisy Channel Spelling Correction . Proceedings of the 38th Annual Meeting on Computational Linguistics, 2000.
[3] T. Brants, AC Popat, P. Xu, FJ Och, J. Dean. Large Language Models in Machine Translation . Proceedings of the 2007 Conference on Empirical Methods in Natural Language Processing.
[4] C. Whitelaw, B. Hutchinson, GY Chung, G. Ellis. Using the Web for Language Independent Spellchecking and Autocorrection. Proceedings of the 2009 Conference on Empirical Methods of Natural Language Processing: Volume 2.
