Bluetooth-based wireless audio: what's better?

With the development of technology, the usual "tube" analog headphones go down in history - they are increasingly being squeezed out by Bluetooth wireless-based fellows.

Modern smartphones are deprived of the usual connector for the sake of moisture and dust protection.

The developers are releasing all newer versions of the Bluetooth protocol and all newer versions of codecs, promising “faster, higher, stronger” - lower playback delays and better quality.

Is everything so good? Let's get a look.

Introduction

I will not delve into the technical implementation of the protocols, as well as the boring specifications. Dear ValdikSS , who to a large extent was the inspiration and even the scientific consultant in this article, is preparing an exhaustive material on codecs - and everything will be described in much more detail and technically correct.

I want to tell more about personal experience. Well, a little entertaining (boring?) Practice.

A year and a half ago, I got the idea of ​​aptX. Yes, I read a lot of reviews like this and believed in all these technical bells and whistles and possibilities. I was born a child - and I really wanted to watch TV with headphones at night, without creating noise and without waking anyone in the house.

What is it poured?

Quality

Let's start with the numbers and facts (hello, Wikipedia!)

SBC is a good old codec, mandatory if you follow the A2DP standard. The codec is the result of the work of Frans de Bont (F. de Bont, M. Groenewegen and W. Oomen, "A High Quality Audio-Coding System at 128 kb / s", 98th AES Convention, Febr. 25-28, 1995) and use algorithms described in patent EP-0400755B1 . It is noteworthy that the authors of the patent allow free use of the SBC only in the Bluetooth application; nevertheless, the patent expired on June 2, 2010. Since the A2DP standard is very common, it is extremely difficult to find headphones or speakers that would not have SBC support.

The codec provides a sampling frequency of 16, 32, 44.1, 48 kHz with a flow rate of 10-1500 kbit / s. Yes, you heard right. Up to 1500 kbps. The codec simply does not have a limit on bitrate. But more about that later.

The aptX codec was developed in 1988 at the Royal University of Belfast.. Yes, there was still about a decade before Bluetooth, so the codec was used in professional audio equipment. Currently, rights are owned by Qualcomm, and therefore use requires licensing and license fees. As of 2014, the cost is approximately as follows: a one-time payment of $ 6000 and ≈ $ 1 for each device released for batches of up to 10,000 devices. For this reason, many devices with Snapdragon chips 835, 845, 821, 820, 810, 805, 801, 800, 650, 615, 410 are quite possible and support aptX, but it was not activated there because the license was not purchased. About this is also below.

With a bit depth of 16 bits and a sampling rate of 48 kHz, the codec can provide a stream rate of 384 kbps (dual channel).

List of products officially supporting aptX. On Aliexpress you can find a lot of unknown systems with support for aptX, but be prepared for the fact that in fact there will be the same good old SBC - and no more.

aptX HD - the same codec, but with a different encoding profile, has a bit rate of 576 kbps, support for a sampling rate of up to 48 kHz and a bit depth of up to 24 bits. Some people call this codec aptX Lossless - but this is complete nonsense, if only because it is not currently possible to reach the value of a stream that could carry lossless data. A special advantage of this codec is the adjustable coding delay, which can be reduced to 1 ms at a sampling rate of 48 kHz. Also, the codec is extremely advantageous in terms of CPU utilization, which is an advantage over MP3 and AAC.

List of products officially supporting aptX HD . It is rather small.

aptX Low latency (or LL) is a special version of the codec that allows you to reduce the audio delay time to less than 40 ms. List of products officially supporting aptX LL .



Here she is. This picture in due time has bought me with guts. Delays! After all, who wants to hear the sound of an explosion in some kind of action movie, the cry of a monster in horror or the roar of the crowd at a football match, when it was all over?

But is this really all about it?

Unfortunately no.

As with any marketing material, the numbers are far-fetched. The delay largely depends on system buffering and codec implementation. So, the delay with SBC may well be at the level of less than 40 ms, which, taking into account the standards of television broadcasting (+40 ms ... −60 ms), is quite acceptable.

Summarizing:

1. No existing codec can be better than wired technology, since no codec can achieve true lossless compression.
2. The most popular codec is SBC. He is the most flexible in the settings. And despite the fact that aptX was released earlier, he could not beat the popularity of the SBC, apparently because of the free of charge last.
3. The sound quality is extremely dependent on the implementation of the codec, as well as on the hardware performance of the headphones / speakers in general - if the speaker itself is weak, you will not improve the quality with any codec. Therefore, in the future, comparing the quality, we will talk about playing the same content from the same source on the same speakers / headphones, but with different codecs.

Practical and very subjective results

The information is based on the already mentioned one and a half year experience in operating, comparing and attracting outside listeners.

The experience is based on listening to lossless on the SONY Walkman NWZ-A17 player, where you can choose a codec, as well as watching various programs with audio output through Avantree Priva III.

Headphones were three: Sennheiser PMX 60, Koss Porta Pro and Koss UR-20.

Jabra BT3030 (SBC) and Avantree Clipper Pro (aptX) were used as wireless signal receivers.

Also used was a Voombox Outdoor speaker (SBC) and Aftershokz Trekz Titanium bone conduction headphones (aptX).

All equalizers and improvers were turned off - and this is important.

Total:

1. The quality of the sound played when wired is always better. This is without a doubt.
2. The difference between SBC and aptX is extremely difficult to hear - and only in the case of some types of music. For example, the author of the article clearly heard the difference on cello solo in classical compositions, while the difference for the violin and low-frequency instruments was less noticeable. In modern genres - pop, electronic music and rock - the difference is not audible. In some cases, subjectively, it seemed that the SBC transmits sound better than aptX.
3. The delay between SBC and aptX can be noticed only if it is connected to the same source and different receivers are inserted into different ears (well, the left channel is SBC, and the right one is aptX for example). Delay with a picture is almost impossible to see, and therefore the story is that aptX is designed for dynamic scenes and content - a myth.
4. Surprise caused the sound quality at a fairly cheap and "not famous" Voombox Outdoor. Apparently, this is the successful implementation of SBC, which was mentioned above.
5. The implementation of aptX in bone-conductive headphones is completely incomprehensible - the technology is very specific, and therefore the loss in quality is significant because of the technology itself. Taking into account the small range of "range" of the device, an extremely poor implementation of pairing with two devices, I can state that Aftershokz is a company that invests more in marketing than in development.

I do not argue that if you connect all sorts of spectral analyzers and stuff, you can and should see the difference. But the human ear, and even worse - the average human ear is not a spectral device, and therefore does not hear all these nuances.

Practice: fix what can be fixed

Part 1. Turn on aptX

As already mentioned, in some devices the use of aptX is disabled, probably to avoid patent prosecution.

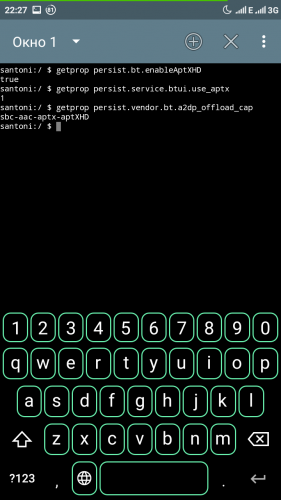
This issue can be resolved quite simply - by slipping the library device into the codec to implement the work and setting the option of working with this codec in build.prop.

On the Internet there are a large number of solutions of this nature. I took the liberty of combining them into one, while implementing it as a module for Magisk. Yes, I really love this project and I believe that the implementation of changes in the system in the form of Magisk modules is a better and safer solution with the ability to save the system as much as possible in its original form and easy way to roll back.

The module can be downloaded from here.. Yes, I know about the githab. And no, as long as I do not have time to upload it there.

Entries to build.prop, including aptX, and, if possible, aptX HD, will be emulated automatically by the module.

Part 2. Increasing the SBC bit rate

As previously reported, the SBC codec is fundamentally free of bitrate restrictions. However, manufacturers usually set a limit of 342 kbps for mono and 345 kbps for stereo in order to ensure reliable operation with all types of receiving devices.

At the same time, the A2DP v1.2 specification, which was active from 2007 to 2015, requires all decoders to work correctly with bitrates up to 320 kbps for mono and 512 kbps in the case of a stereo signal.

In the new version of the specification, there is no limit on bitrate at all. It is assumed that modern headphones, released after 2015 and supporting EDR, can support bitrates up to 730 kbps.

In fact, this is certainly not the case. In an extensive study by ValdikSSIt was found that almost all receiving devices work reliably with 454 kbit / s bitrate values, and a sufficiently large number - with 507 kbit / s bitrate.

In his research, ValdikSS also showed that, contrary to the conventional wisdom about the sound quality of the aptX codec, on some files it may produce worse results than SBC with a standard bitrate of 328 kbps, and switching to high-bit SBC, you will get a sound that is often superior aptX, on any headphones.

ValdikSS based on this data sent comments to the developers of Lineage OS and to Google, but at the moment there was no reaction.

Thus, we can only manually make modifications to the Bluetooth stack.

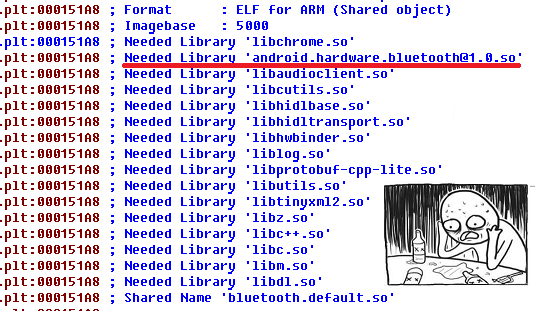
We will need IDA Pro with the ability to decompile ARM, any HEX editor (I used WinHEX) and the bluetooth.default.so file from our device. Usually it is located along the path / system / lib / hw and less often - also along the path / system / lib64 / hw (root-access is definitely needed).

So, open the bluetooth.default.so file. The operations and modifications described below apply only to the original Android stack (bluedroid). If you see the line “Needed Library 'com.qualcomm.qti.bluetooth_audio@1.0.so'” or similar in IDA Pro, with high probability, this instruction will not help you.



Our first task is to replace the Joint Stereo with a Dual Channel in a standard configuration.

We will work with the bta_av_build_src_cfg function .

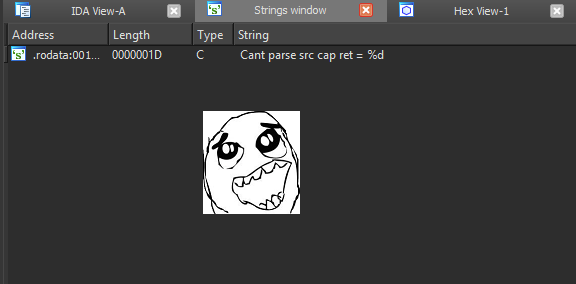
To find this procedure in IDA, we use the searchalong the line of the characteristic message to the debug log “Cant parse src cap ret =% d” :





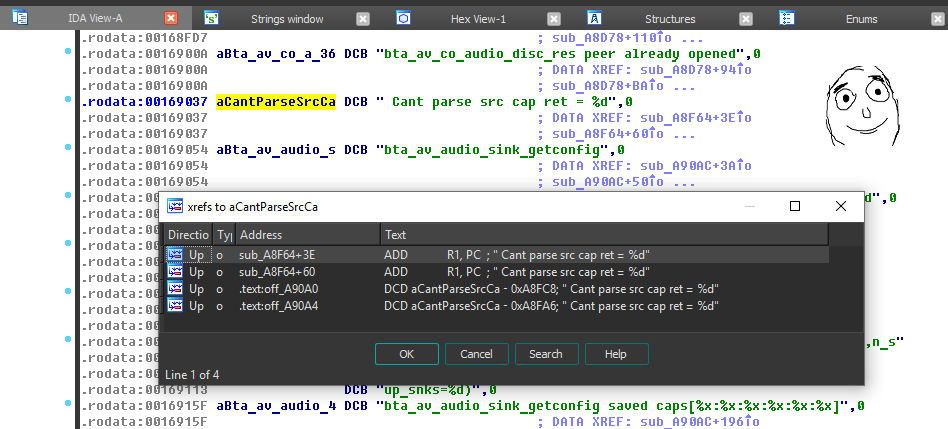
As a result, rather quickly we find the function itself in the form of code:



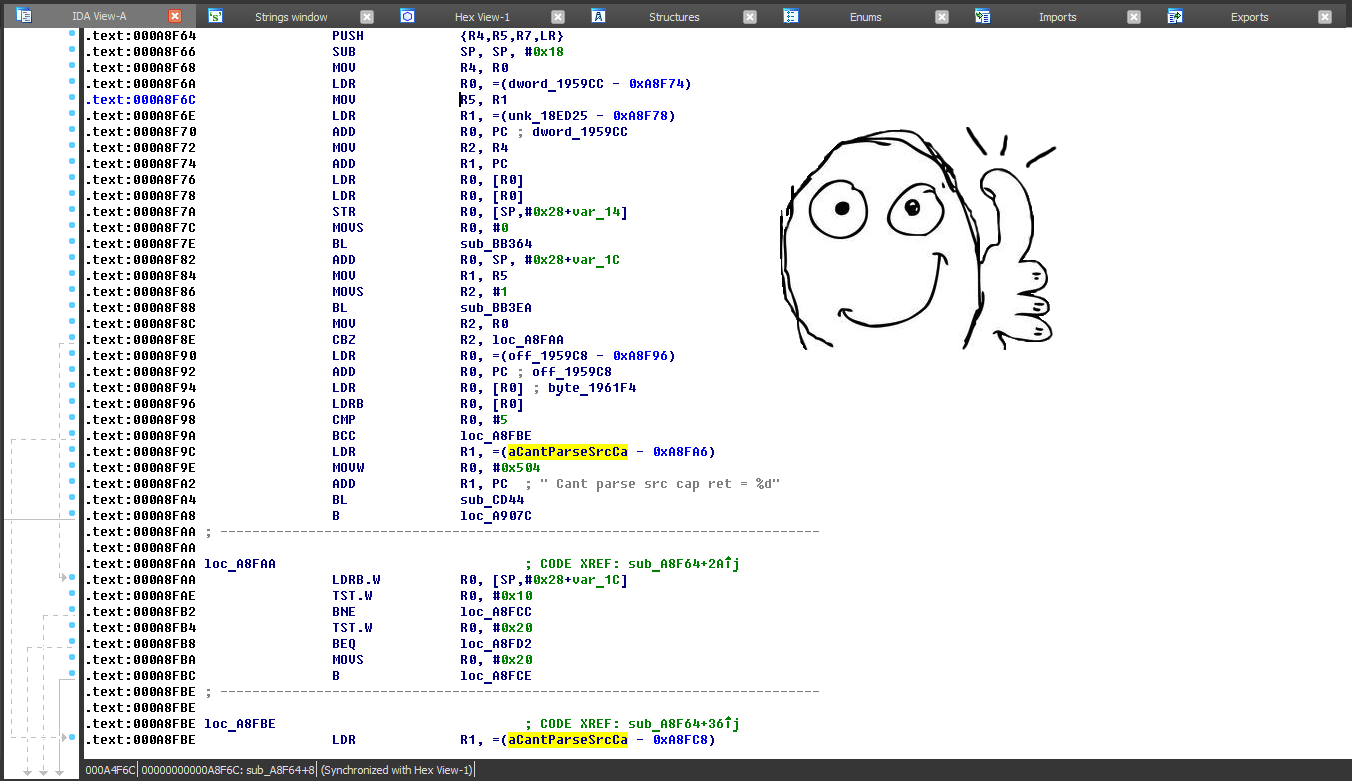
Our task is to replace the original structure of checks

    if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_JOINT)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_JOINT;
    else if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_STEREO)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_STEREO;
    else if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_DUAL)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_DUAL;
    else if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_MONO)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_MONO;</code>
на
<code>    if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_DUAL)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_DUAL;
    else if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_STEREO)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_STEREO;
    else if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_DUAL)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_DUAL;
    else if (src_cap.ch_mode & A2D_SBC_IE_CH_MD_MONO)
        pref_cap.ch_mode = A2D_SBC_IE_CH_MD_MONO;

This can be done in several ways.

The first one is the substitution of instructions TST.W R0, # 1 by TST.W R0, # 4 and MOVS R0, # 1 by MOVS R0, # 4 in the sequence of checks:



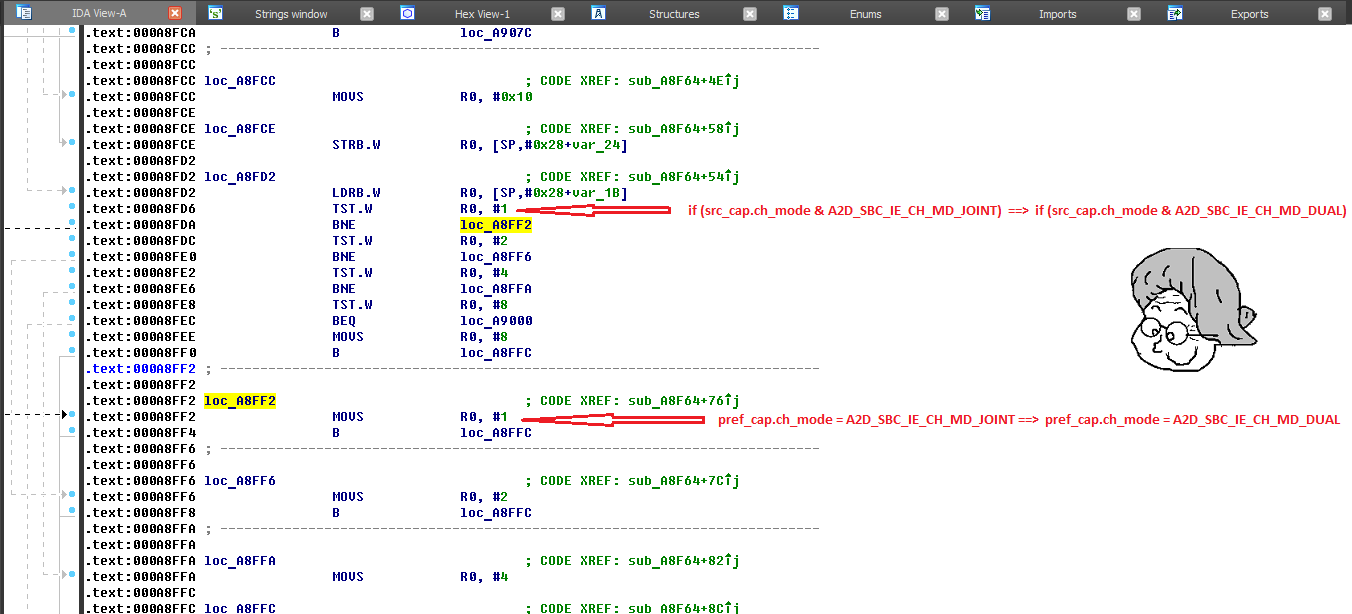
In the bytecode, this is replacing x01 by x04. It is important to note the characteristic sequence of bytes by which this pattern can be found. Without going deep into details, I’ll say that this is essentially a search for a sequence

10 20 8D F8 04 00 9D F8 0D 00 10 F0 01 0F ?? ?? 10 F0 02 0F ?? ?? 10 F0 04 0F ?? ?? 10 F0 08 0F ?? ?? 08 20 ?? ?? 01 20 ?? ?? 02 20 ?? ?? 04 20

and replacing it with

?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? 04 ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? 04 ?? ?? ?? ?? ?? ?? ?? ?? ??

However, this method has drawbacks.

A number of compilers change the sequence of command execution depending on optimization. And in this case, it is not possible to find the desired pattern, and sometimes the checking mechanism in the structure is generally entered into the inline code. Therefore, it is more reliable to change the constant btif_av_sbc_default_config .

To begin with - we will find it. It is at the very beginning of our function, because

void bta_av_build_src_cfg (UINT8 *p_pref_cfg, UINT8 *p_src_cap)
{
    tA2D_SBC_CIE    src_cap;
    tA2D_SBC_CIE    pref_cap;
    UINT8           status = 0;
    /* initialize it to default SBC configuration */
    A2D_BldSbcInfo(AVDT_MEDIA_AUDIO, (tA2D_SBC_CIE *) &btif_av_sbc_default_config, p_pref_cfg);
    /* now try to build a preferred one */
    /* parse configuration */
    if ((status = A2D_ParsSbcInfo(&src_cap, p_src_cap, TRUE)) != 0)
    {
         APPL_TRACE_DEBUG(" Cant parse src cap ret = %d", status);

Here it is:





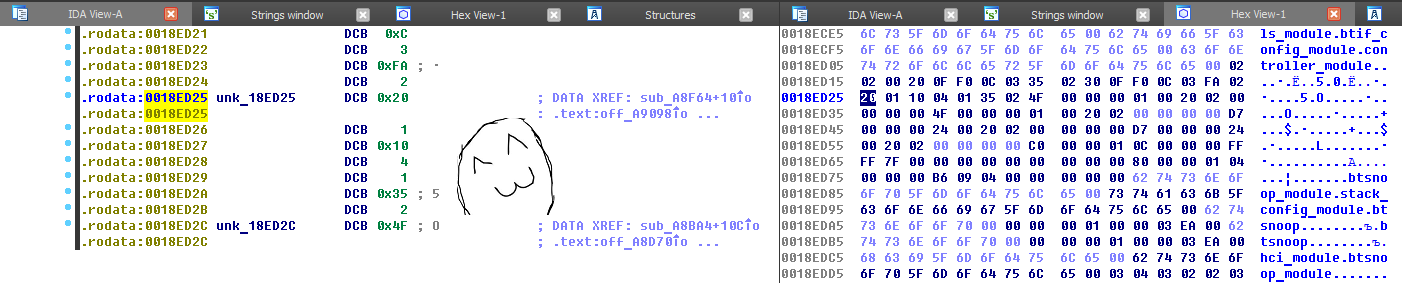
It can be seen that btif_av_sbc_default_config itself is a sequence of bytes 20 01 10 04 01 35 02, while the first byte encodes the sampling frequency and can be 10 (48 kHz) and 20 (44 kHz), and therefore not specific. Thus, our task is to replace the sequence
01 10 04 01 35 02
with
04 ?? ?? ?? ?? ??

It. This will allow to change the logic of the structure in the same way, but the optimization of the compiler will not cause problems.

In some cases, the initiator of the connection are the headphones or speakers themselves. In this case, the mode is determined by the bta_av_co_audio_init function .

The function is characterized by the string “bta_av_co_audio_init:% d” and is easily found in the code:


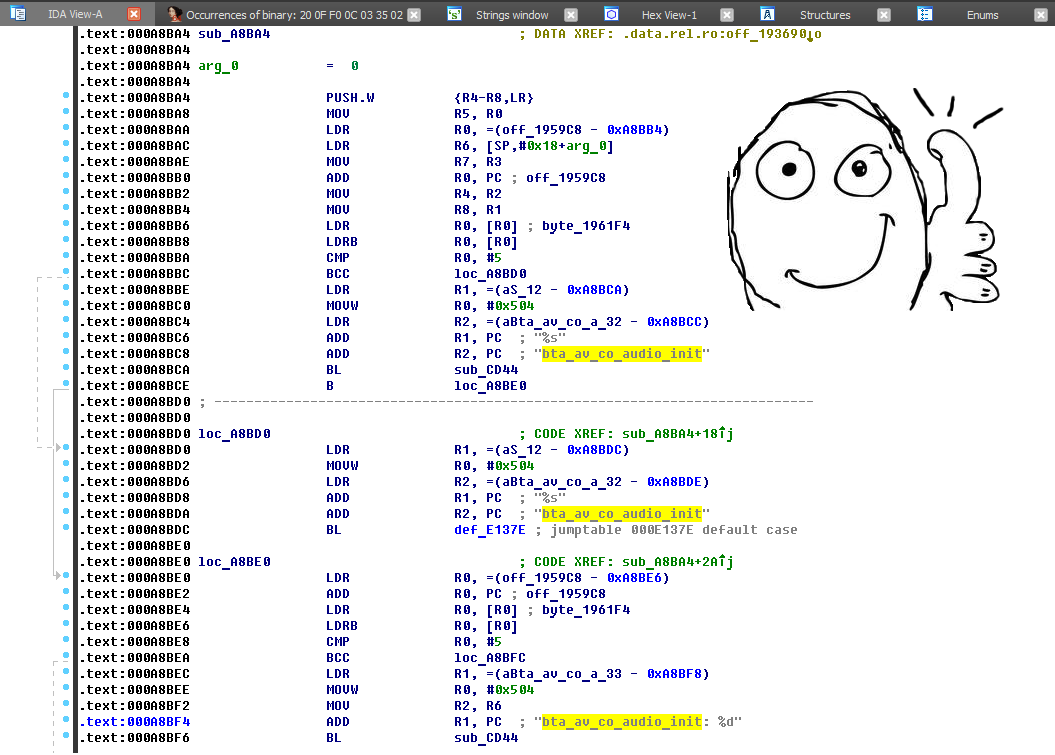
The possible connection modes are listed in the following command:

    switch (index)
    {
    case BTIF_SV_AV_AA_SBC_INDEX:
        /* Set up for SBC codec  for SRC*/
        *p_codec_type = BTA_AV_CODEC_SBC;
        /* This should not fail because we are using constants for parameters */
        A2D_BldSbcInfo(AVDT_MEDIA_AUDIO, (tA2D_SBC_CIE *) &bta_av_co_sbc_caps, p_codec_info);
        /* Codec is valid */
        return TRUE;

while the constant bta_av_co_sbc_caps has the following structure :

const tA2D_SBC_CIE bta_av_co_sbc_caps =
{
    (A2D_SBC_IE_SAMP_FREQ_44), /* samp_freq */
    (A2D_SBC_IE_CH_MD_MONO | A2D_SBC_IE_CH_MD_STEREO | A2D_SBC_IE_CH_MD_JOINT | A2D_SBC_IE_CH_MD_DUAL), /* ch_mode */
    (A2D_SBC_IE_BLOCKS_16 | A2D_SBC_IE_BLOCKS_12 | A2D_SBC_IE_BLOCKS_8 | A2D_SBC_IE_BLOCKS_4), /* block_len */
    (A2D_SBC_IE_SUBBAND_4 | A2D_SBC_IE_SUBBAND_8), /* num_subbands */
    (A2D_SBC_IE_ALLOC_MD_L | A2D_SBC_IE_ALLOC_MD_S), /* alloc_mthd */
    BTA_AV_CO_SBC_MAX_BITPOOL, /* max_bitpool */
    A2D_SBC_IE_MIN_BITPOOL /* min_bitpool */
};

The constant is easily located in the code, in my case it is 20 0F F0 0C 03 35 02:



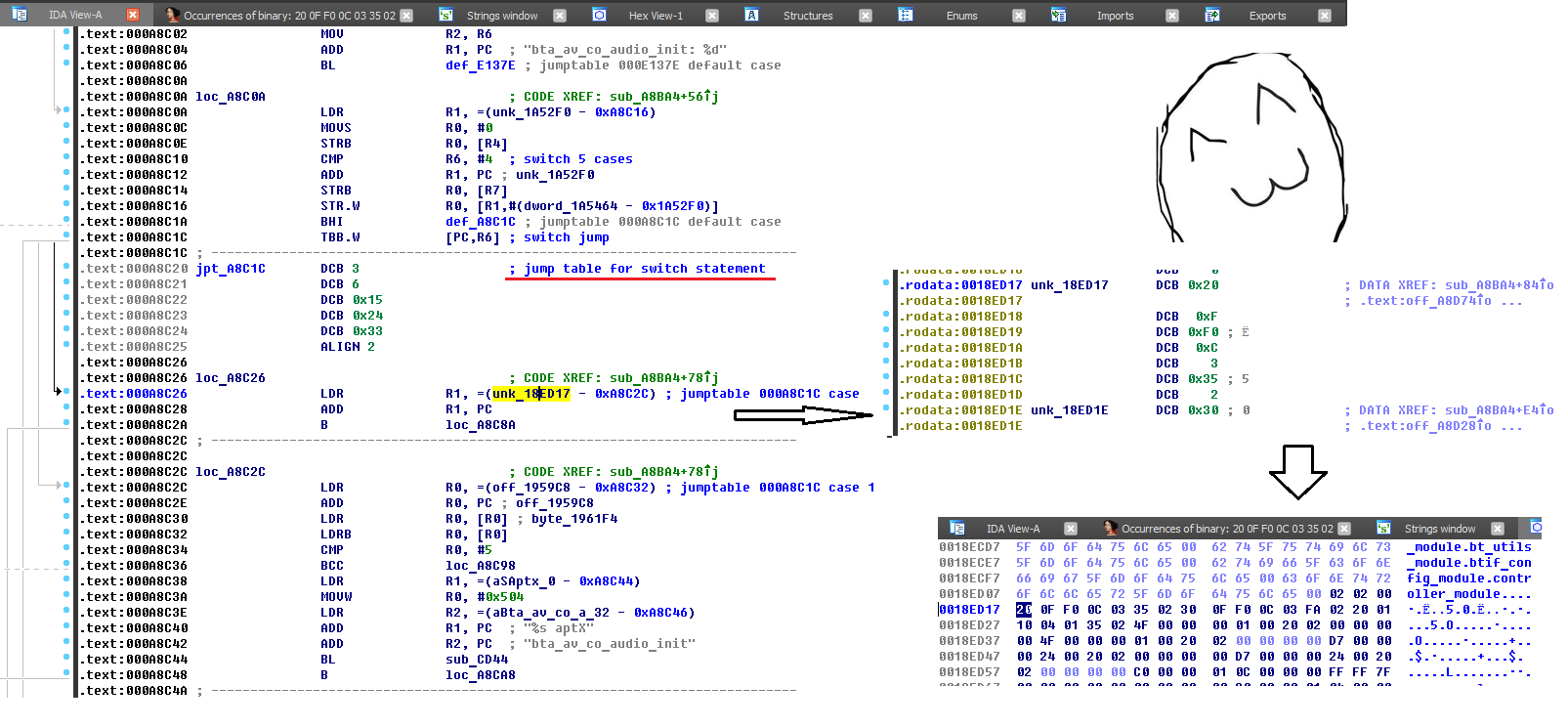
Pay attention to byte 0F - it provides the ability to connect with any of the allowed modes, since

x0F = A2D_SBC_IE_CH_MD_MONO | A2D_SBC_IE_CH_MD_STEREO | A2D_SBC_IE_CH_MD_JOINT | A2D_SBC_IE_CH_MD_DUAL = x08 | x02 | x01 | x04

Our task is to change this value in this way:

x0F = A2D_SBC_IE_CH_MD_DUAL = x04 

Therefore, it is necessary to replace

?? 0F F0 0C 03 35 02
with
?? 04 ?? ?? ?? ?? ??

So, we forced the stack to connect in the Dual Channel mode both in the case of the connection being initiated by the device, and in the case of the connection being initiated by the receiving signal side.

Now you need to remove the restrictions in bitrate or raise its upper threshold.

It is necessary to process btif_media_task_get_sbc_rate . Similarly, looking for the characteristic string “non-edr a2dp sink detected, restrict rate to% d”, we look for the function in the code:


The bitrate limit is expressed in the
UINT16 rate = DEFAULT_SBC_BITRATE line (which in turn is 328 kbit / s ).

In the code it is like this:



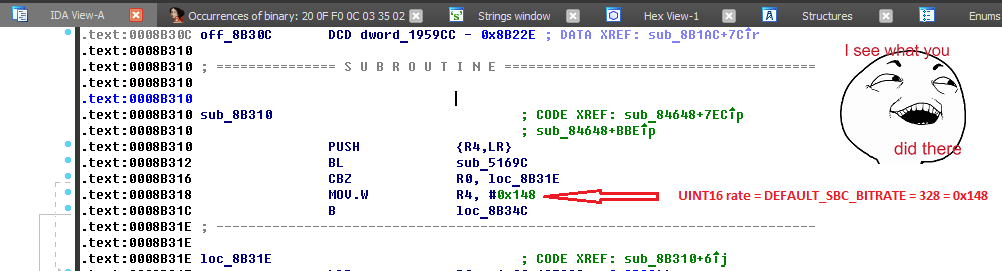
Let's change this value to 454 kbps - this is higher than the standard one and works with the vast majority of receiving devices. To do this, replace the bytes

B1 4F F4 A4 74 ?? E0
with.
?? ?? ?? E3 ?? ?? ??

Also search for the pattern

E0 4F F4 A4 74 ?? E0
and replace it with
?? ?? ?? E3 ?? ?? ??
- this is required for a number of devices.

The value of E3 may be different depending on the desired maximum bitrate:

• E3 - 454 kbps
• F1 - 482 kbps
• F3 - 486 kbps
• 10 - 576 kbps
• 48 - without restrictions

In general, this is determined by the byte code of the operation MOV.W R4, XXX.

In practice, it is worth experimenting and choosing the maximum value at which in all your receiving devices there is a stable signal reception, there is no crack, interruption and distortion.

In all the receivers in my experiment (I indicated them above), this value was 576 kbps, the signal source was the Xiaomi Redmi 4x MIUI10 Android 7.1 phone.

Based on the described actions, was a generic patch created that finds the specified patterns in Bluetooth.default.so and replaces them? including forced Dual Channel mode and setting a bitrate limit of 454 kbps. If necessary, the value of the limit can be easily changed on the basis of the search and replacement of the corresponding byte - the attentive reader will do it without difficulty.

I emphasize: the patch works only in the case of a bluedroid stack and most likely will not be successful in the case of the Fluoride stack and versions of Android 8 and newer.

The patch can be downloaded from here .

It is strongly recommended to replace the original file as Magisk modules, for myself I did it as follows . note: these modules are made by me for the phone Xiaomi Redmi 4x 3/32 GB with the current global stable firmware MIUI 10 as of this writing. In your case, you will have to replace the bluetooth.default.so file with your own patched one as described above. It is also possible that the file will have to be duplicated along the path / system / lib64 / hw - this depends on the model and firmware version of your phone.

This approach using Magisk modules allows you to easily change the maximum bitrate and disable changes altogether if it turns out that one of the receiving devices does not support Dual Channel.

Conclusion

At the moment, in pursuit of sales, many companies are submitting some technological innovations as a justification for a higher price.

In practice, it turns out that existing, cheaper technologies are not fully developed, and technological innovations are not fully implemented, which significantly affects the quality.

Very often, users experience a “placebo effect”, convincing themselves of the perfection of a particular product just because it is newer or more colorfully presented. In fact, this quality is imaginary.

Despite the obvious deterioration in the quality of wireless transmission of sound compared to the wired version, it seems that modern device manufacturers are aiming at a complete transition to wireless technology. At the same time, marketing tricks are used to justify the price increase: protection against immersion of the telephone in the water (how can you talk underwater? Why drop a device into the water?), Use of more expensive codecs, etc. At the same time, the potential of the existing popular SBC codec is not fully utilized.

We didn’t manage to get any clarification from Google about the bitrate of 328 kbps, nor get rid of this limit and add the option to enable Dual Channel in the Bluetooth menu from the Lineage OS developers.

Thanks to everyone who read to the end!

Some continuation, caused by the discussion in the comments and the space for the LDAC codec, is here .