There are and no
First, an example of an olympiad problem in logic. On the island live the sages and liars. Moreover, their yes and no sound like a bang and a bang. Which of them exactly is unknown.
We decide. The sage will answer as follows: (A = A), (A ≠ not A). The answer of a liar in this case: (A ≠ A), (A = not A). Suppose that in their language, pif - yes. Then the sage will answer the question (pif - yes?) If in their language (a pif - this is not), then his answer will be the same: a pif. A liar will always express non-existent (that which is not), saying puff.
So, the construction of truth (identically true formula) A = A, lies (identically false formula) A ≠ A. The same formulas allow you to transfer logical primitives: there is A, no A. Here is an example in python.

You can express everything said this way:
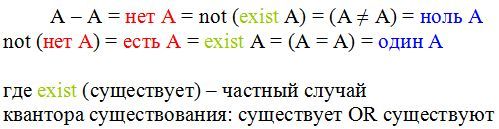
Is it possible to go further by constructing more complex things on this basis? Of course. For example, take the uniquely closed transformation T, in which transitions (the term cybernetics) are presented in a tabular form:
(U: S-> Z), (U: Z-> S), (U: W-> Z), (P: S-> Z), (P: Z-> W), (P: W-> S), (V: S-> S), (V: Z-> Z), (V: W-> Z)
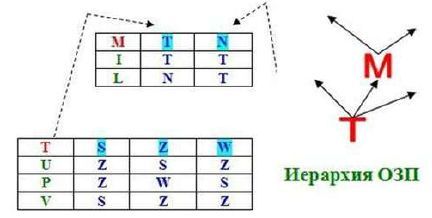
I note that these transitions reflect the same meaning as morphisms in category theory. If we apply a function to an argument of a function, we get only the value of the function: (F: X-> Y) or (Y = F (X)).
It would seem that such a uniquely closed transformation is completely devoid of contradiction (identically false formula). But we ask ourselves: how then to interpret, say, the transition (U: S-> Z)? It was S, ceased to be S, Z arose. We get all the same primitives: there is S, there is no S & there is no Z, there is Z. In other words, the variable T sequentially takes (speaking only of the existing) values of S, Z.
You can see that there is (exists) here is interpreted as a predicate: (S - is) or (S - is not). I repeat (there exist OR exist), i.e. the existential quantifier is not the same as (exists). In fact, one or more of one is not the same as one.
Are these existing and not applicable to uniquely closed transformations? Yes. So, for a uniquely closed transformation M, one of the states is our T. And you can express its existence and non-existence also: there is T = (T = T), there is no T = (T ≠ T)
We decide. The sage will answer as follows: (A = A), (A ≠ not A). The answer of a liar in this case: (A ≠ A), (A = not A). Suppose that in their language, pif - yes. Then the sage will answer the question (pif - yes?) If in their language (a pif - this is not), then his answer will be the same: a pif. A liar will always express non-existent (that which is not), saying puff.
So, the construction of truth (identically true formula) A = A, lies (identically false formula) A ≠ A. The same formulas allow you to transfer logical primitives: there is A, no A. Here is an example in python.

You can express everything said this way:
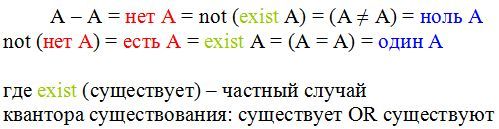
Is it possible to go further by constructing more complex things on this basis? Of course. For example, take the uniquely closed transformation T, in which transitions (the term cybernetics) are presented in a tabular form:
(U: S-> Z), (U: Z-> S), (U: W-> Z), (P: S-> Z), (P: Z-> W), (P: W-> S), (V: S-> S), (V: Z-> Z), (V: W-> Z)

I note that these transitions reflect the same meaning as morphisms in category theory. If we apply a function to an argument of a function, we get only the value of the function: (F: X-> Y) or (Y = F (X)).
It would seem that such a uniquely closed transformation is completely devoid of contradiction (identically false formula). But we ask ourselves: how then to interpret, say, the transition (U: S-> Z)? It was S, ceased to be S, Z arose. We get all the same primitives: there is S, there is no S & there is no Z, there is Z. In other words, the variable T sequentially takes (speaking only of the existing) values of S, Z.
You can see that there is (exists) here is interpreted as a predicate: (S - is) or (S - is not). I repeat (there exist OR exist), i.e. the existential quantifier is not the same as (exists). In fact, one or more of one is not the same as one.
Are these existing and not applicable to uniquely closed transformations? Yes. So, for a uniquely closed transformation M, one of the states is our T. And you can express its existence and non-existence also: there is T = (T = T), there is no T = (T ≠ T)
