Java implementation of a hashed binary tree
A friend of mine likes to say (I don’t know if these are his words or he took them somewhere) that programmers go for two reasons: if you want to become a hacker or if you want to write games. My second case. I have always been interested in game development, and the part that is responsible for artificial intelligence in games. I spent a lot of time studying path finding algorithms. Implementing the next version of the A * algorithm in Java, I came across an interesting situation related to the TreeSet and TreeMap collections.
I want to immediately introduce two concepts that I will use throughout the article: a search for equality and a search in comparison . Equality SearchI will call a search in a collection where equals and hashCode methods are used to compare elements . Search by comparison or search based on comparison, I will call the search for an element in the collection, where the methods compare and compareTo are used to compare elements .
The A * algorithm uses two collections to store waypoints: an open list and a closed list. Roughly speaking, a waypoint has three important attributes for us: the X coordinate, the Y coordinate, and the value of the metric function - F. For a closed list, you need to perform only two operations, add and search. With an open list, things are a little more complicated. With an open list, in addition to the operations of adding and searching for an element, it is also necessary to find the smallest point by the value of the metric function.
For a closed list, select HashSet; everything is obvious here; for add and search operations, it’s great if you have written a good hash function. There are difficulties with choosing a collection for an open list. If you choose a HashSet, as for the closed list, then we will get the best asymptotic behavior for the insert, search and delete operations - O (1), however, the minimum search will be performed in O (n). When choosing TreeSet or TreeMap, we will have O (log (n)) for insertion and search, but for searching and deleting the minimum we will have all the same O (log (n)). See the asymptotics of various collections here .
Another important detail related to TreeMap and TreeSet- All operations with these collections use comparisons. Thus, if the search interests us taking into account the coordinates of the points, then to find the minimum we use the value of the metric function, and this will lead to the fact that the operation may not be performed for the point at which this value was changed. Moreover, when inserting new values, we can get an incorrectly constructed tree: if we take points with the same coordinates equal and take this into account in the comparator, then inserting a new value into the tree will not happen.
It makes sense to use a collection based on a binary tree, since elements are not added to the open list so often, while the search for the minimum element by the value of the metric function is performed at each iteration of the search algorithm. This is due to the fact that adding to the open list depends on the presence of a similar (in coordinates) element in the closed list, which grows over time and there are more and more points in it - the more points in the closed list, the less likely it is to add the element to the open list. But I would also like to have the advantages of the HashSet collection .
I decided to generalize the task. Let some data structure be defined in which there is a set of fields. Let also some fields determine the equivalence relation of two elements of a given structure, while other fields determine order relations (in other words, the equals and hashCode methods use the same fields of the object, and the compare and compareTo methods use the other).
Objective: to implement a data structure in which the operation of searching for an element on the basis of equality is performed with the asymptotic behavior of O (1), and the operations of insertion and deletion work taking into account operations and comparison and equality, and build a binary tree in such a way that the smallest element would be the root of the tree .
Since for my purposes I need to store points in an open list taking into account their coordinates, I can uniquely determine the hash function based on the size of the patency map so that it will not have collisions, so I decided to set the maximum number of elements in the collection constant .

The idea is very simple: we will put the elements of the collection into an array on the basis of the hash, and immediately put the same elements in a binary tree. We need an inner class for packing elements into tree nodes:
Type V defines an element of the collection; it must extend the Comparable class so that it can be compared to build a tree.
In the class, in addition to pointers to the left and right descendant, there is a pointer to the ancestor. This is done to optimize the process of removing an element from the tree - having the progenitor of the deleted element can be excluded from the deletion algorithm bypassing the tree starting from the root, you can use an array of elements to search. A field with the name k contains the number of subtree nodes if they are not consecutive increasing nodes in the left child.
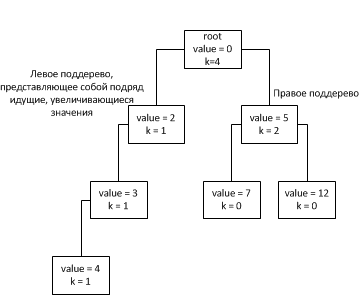
Inside the collection, there should be a pointer to the root of the tree and an array of elements of the collection, where null is stored in empty cells, and instances of the Node class are in filled cells, where the value of the added element will be stored in the data field (or rather, the value of the pointer to the object instance):
Like type V, type E defines a collection item. By default, the collection is empty, so the pointer to the root element is null and the array is also filled with null values . An abstract class with an abstract getElementHash method that allows you to override the calculation of the hash code.
Now to the methods. AddElement method :
In the method, we get the hash code of the element to be added. We create a new tree node with a new element as data and add it to the tree and to the array, where the hash code defines the index in the array. The insertion of an element into the array has the asymptotics O (1), the insertion into the tree has O (log (n)), the total asymptotics is O (log (n)). RemoveElement
method :
Here, using the hash code of the element to be deleted, the tree node to be deleted is extracted from the array. Using the ancestor of the node to be deleted, we delete the element, during which we have to call the subtrees 2 times, each of the operations in the worst case has an asymptotic behavior - O (log (n)). As a result, the method has the asymptotics O (log (n)).
The connectNodes method joins both a single node and a subtree. Moreover, the binding occurs using comparison. Thus, the smallest element is always at the top of the tree. ConnectNodes
method :
The connectNodes method should be given special attention. Adding a new element is performed using this method with respect to the root and the new element. We believe that the tree is not empty:
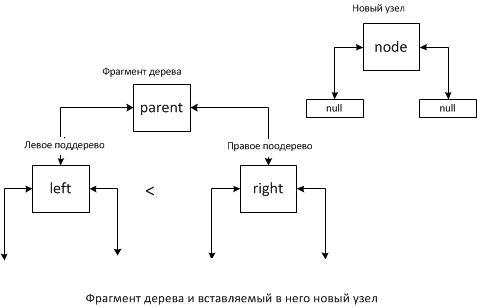
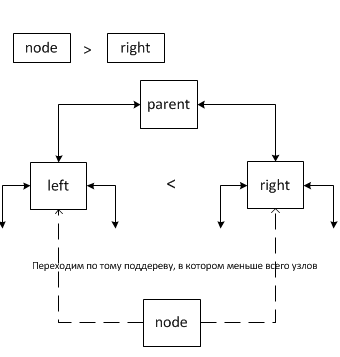
4 cases are possible:
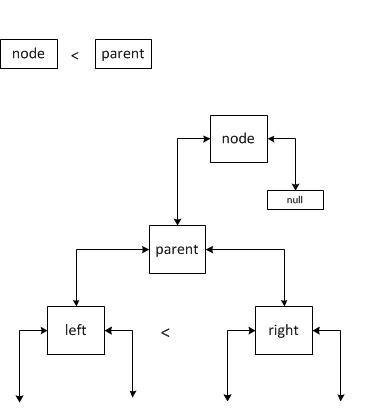
Case 1.
In this situation, the parent becomes the left descendant of the new element, if parent is the root of the tree, then the new, added element will be the new root, respectively.
Case 2.
There are two possible options: the right child is defined and the right child is not defined. If the left descendant is not defined, then we consider that the left descendant is of greater importance to the new node. In both situations, the new element becomes the left child of the parent, and left (which was the left child before adding) becomes the right child. However, in the second case, you need to join the old right descendant right to the new right descendant left. Joining left to right will occur according to the same rules as in the described cases.

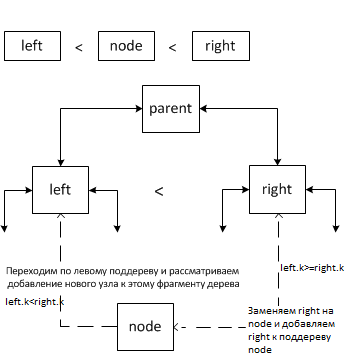
Case 3
In this case, either the left subtree is jumped and a new node is added to it if there are fewer nodes than the right subtree, or the right subtree right is replaced with the inserted node node and the right subtree right is added to it.
Case 4.
In this case, the transition is performed along the subtree in which there are the least nodes. The number of nodes accumulates in the field k.
Now we estimate the asymptotic behavior of the connectNodes method . In the best case, when nodes without descendants are added to the tree in decreasing order, the asymptotic behavior will be O (1), since in this case, put the new element in the place of the grandparent. If we are talking about associating a node with descendants and smaller than the progenitor, then you will need to go through the subtree of the node. For case 2 in paragraph a)the asymptotics is O (1), and in step b) you need to again go through the subtree of the inserted node.
Note that the field k at the nodes increases for all cases except the 1st, this is done so that the tree is filled symmetrically, but without violating the increasing order of the left subtree if one occurs.
To assess the complexity of the passage through the tree, it is enough to evaluate its height. The height of the tree will be the desired asymptotic behavior. A separate issue is the presence of the length of the sequence on the left subtree. If we take into account the presence of such subtrees, in the worst case, the asymptotic behavior of the binding can be considered as the asymptotic behavior of the binding with the subtree that we want to bind, and in the best case, as O (1) (2 case).
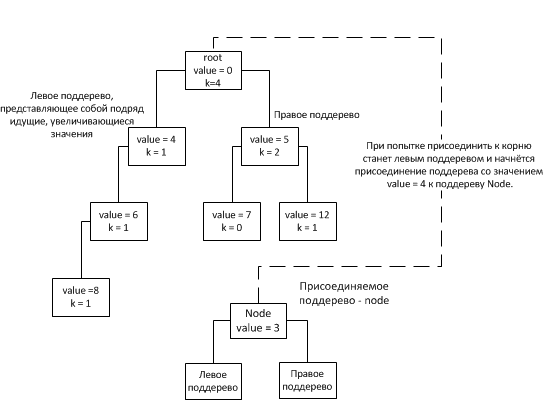
Since when connecting nodes we are dealing with nodes inside the tree, the height of any subtree can be considered not to exceed the height of the tree itself. Thus, having estimated the height of the entire binary tree, we obtain the asymptotic behavior of the connectNodes method. Due to the fact that the selection of the subtree for insertion is selected based on the field k of the node (which stores the size of the subtree except for consecutively increasing increasing nodes, they are considered as one node), the tree tends to fill its next level only after filling the previous one (except, of course, described above case 1). Thus, the tree will have the form:
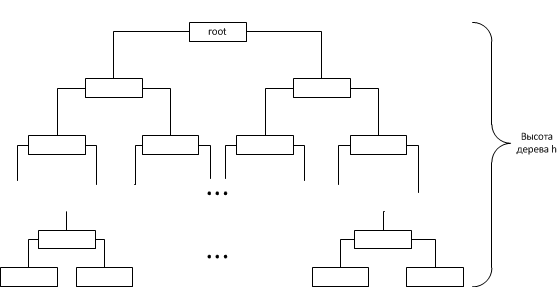
Thus, if n is the number of nodes in the tree, then . From which it follows that the height of the tree
. From which it follows that the height of the tree . It follows that the asymptotic behavior of the connectNodes method is O (log (n)).
. It follows that the asymptotic behavior of the connectNodes method is O (log (n)).
An element can be searched not in a tree, but in an array based on a hash code; therefore, the search operation has the asymptotics O (1). And since the tree is organized as a binary one, the root always contains the minimum element in comparison and the asymptotic behavior of the minimum search is O (1). I note that the removal of the minimum element has the asymptotics O (log (n)), since when deleting it is required to reorganize the tree, starting from the root using the connectNodes method .
At first glance, the operation to delete the minimum element in the implemented collection has worse asymptotics than the HashSet collection, but do not forget that before you remove the minimum element, you first need to find it, and for this you need to perform operations with the asymptotics O (n). Thus, the final asymptotic behavior of the operation to remove the minimum element in the HashSet collection will have the form - O (n).
Checking for the presence of an element in the collection, as mentioned above, is carried out on the basis of checking for null the element of the array at the index determined by the hash code of the element. The verification is performed by the contains method and has the asymptotic behavior of O (1):
Also, based on the hash code, a search is performed for equality with what with the same asymptotics using the getElement method :
The implemented collection is not without flaws. It requires more memory, it needs a hash function without collisions, and to implement enumeration of elements it is necessary to implement a tree traversal, which is also not a pleasure, but this collection is intended for other purposes. The main advantage is the ability to search for elements of the same type according to different criteria with the best asymptotics. As applied to my task, it was a search for equality based on coordinates and a search for a minimal element based on a comparison of the values of a metric function.
In the end, I’ll give the results of testing the collection for performance compared to the LinkedHashMap , TreeSet, and HashSet collections . All collections were filled with 1000 values of type Integer and, with filled collections, the following set of operations was carried out:
The test results are shown in the table:
As a result, we have more than 2 times higher speed of the HashTree collection compared to LinkedHashMap and 1.27 times faster compared to TreeSet ( it makes no sense to consider a HashSet at all). Checks were performed on a machine with 4GB of RAM and an AMD Phenom (tm) II X4 940 processor, OS - 32-bit Windows7 Professional.
I want to immediately introduce two concepts that I will use throughout the article: a search for equality and a search in comparison . Equality SearchI will call a search in a collection where equals and hashCode methods are used to compare elements . Search by comparison or search based on comparison, I will call the search for an element in the collection, where the methods compare and compareTo are used to compare elements .
The A * algorithm uses two collections to store waypoints: an open list and a closed list. Roughly speaking, a waypoint has three important attributes for us: the X coordinate, the Y coordinate, and the value of the metric function - F. For a closed list, you need to perform only two operations, add and search. With an open list, things are a little more complicated. With an open list, in addition to the operations of adding and searching for an element, it is also necessary to find the smallest point by the value of the metric function.
For a closed list, select HashSet; everything is obvious here; for add and search operations, it’s great if you have written a good hash function. There are difficulties with choosing a collection for an open list. If you choose a HashSet, as for the closed list, then we will get the best asymptotic behavior for the insert, search and delete operations - O (1), however, the minimum search will be performed in O (n). When choosing TreeSet or TreeMap, we will have O (log (n)) for insertion and search, but for searching and deleting the minimum we will have all the same O (log (n)). See the asymptotics of various collections here .
Another important detail related to TreeMap and TreeSet- All operations with these collections use comparisons. Thus, if the search interests us taking into account the coordinates of the points, then to find the minimum we use the value of the metric function, and this will lead to the fact that the operation may not be performed for the point at which this value was changed. Moreover, when inserting new values, we can get an incorrectly constructed tree: if we take points with the same coordinates equal and take this into account in the comparator, then inserting a new value into the tree will not happen.
It makes sense to use a collection based on a binary tree, since elements are not added to the open list so often, while the search for the minimum element by the value of the metric function is performed at each iteration of the search algorithm. This is due to the fact that adding to the open list depends on the presence of a similar (in coordinates) element in the closed list, which grows over time and there are more and more points in it - the more points in the closed list, the less likely it is to add the element to the open list. But I would also like to have the advantages of the HashSet collection .
I decided to generalize the task. Let some data structure be defined in which there is a set of fields. Let also some fields determine the equivalence relation of two elements of a given structure, while other fields determine order relations (in other words, the equals and hashCode methods use the same fields of the object, and the compare and compareTo methods use the other).
Objective: to implement a data structure in which the operation of searching for an element on the basis of equality is performed with the asymptotic behavior of O (1), and the operations of insertion and deletion work taking into account operations and comparison and equality, and build a binary tree in such a way that the smallest element would be the root of the tree .
Since for my purposes I need to store points in an open list taking into account their coordinates, I can uniquely determine the hash function based on the size of the patency map so that it will not have collisions, so I decided to set the maximum number of elements in the collection constant .

The idea is very simple: we will put the elements of the collection into an array on the basis of the hash, and immediately put the same elements in a binary tree. We need an inner class for packing elements into tree nodes:
private static class Node> {
private Node parent;
private Node left;
private Node right;
private int k = 0;
private final V data;
public Node(V data) {
this.data = data;
this.parent = null;
this.left = null;
this.right = null;
}
}
Type V defines an element of the collection; it must extend the Comparable class so that it can be compared to build a tree.
In the class, in addition to pointers to the left and right descendant, there is a pointer to the ancestor. This is done to optimize the process of removing an element from the tree - having the progenitor of the deleted element can be excluded from the deletion algorithm bypassing the tree starting from the root, you can use an array of elements to search. A field with the name k contains the number of subtree nodes if they are not consecutive increasing nodes in the left child.

Inside the collection, there should be a pointer to the root of the tree and an array of elements of the collection, where null is stored in empty cells, and instances of the Node class are in filled cells, where the value of the added element will be stored in the data field (or rather, the value of the pointer to the object instance):
public abstract class HashTree> {
private Node root = null;
private Node[] nodes;
public HashTree(int capacity) {
this.nodes = new Node[capacity];
}
public abstract int getElementHash(E element);
…
} Like type V, type E defines a collection item. By default, the collection is empty, so the pointer to the root element is null and the array is also filled with null values . An abstract class with an abstract getElementHash method that allows you to override the calculation of the hash code.
Now to the methods. AddElement method :
public void addElement(E element) {
int index = getElementHash(element);
if (nodes[index] != null) {
return;
}
Node node = new Node<>(element);
nodes[index] = node;
this.root = connectNodes(this.root, node);
} In the method, we get the hash code of the element to be added. We create a new tree node with a new element as data and add it to the tree and to the array, where the hash code defines the index in the array. The insertion of an element into the array has the asymptotics O (1), the insertion into the tree has O (log (n)), the total asymptotics is O (log (n)). RemoveElement
method :
public E removeElement(E element) {
int index = getElementHash(element);
Node node = nodes[index];
if (node == null) {
return null;
}
nodes[index] = null;
E data = (E) node.data;
Node l = getElemInArray(node.left);
Node r = getElemInArray(node.right);
if (l != null) {
l.parent = null;
}
if (r != null) {
r.parent = null;
}
l = connectNodes(l, r);
if (node.parent == null) {
this.root = l;
if (this.root != null) {
this.root.parent = null;
}
return data;
}
int p = getElementHash((E) node.parent.data);
if (nodes[p] != null) {//здесь сравниваются ИМЕННО значение указателей,
//интересует равенство адресов памяти, а не значений
if (nodes[p].left == node) {
nodes[p].left = null;
}
if (nodes[p].right == node) {
nodes[p].right = null;
}
}
connectNodes(nodes[p], l);
return data;
}Here, using the hash code of the element to be deleted, the tree node to be deleted is extracted from the array. Using the ancestor of the node to be deleted, we delete the element, during which we have to call the subtrees 2 times, each of the operations in the worst case has an asymptotic behavior - O (log (n)). As a result, the method has the asymptotics O (log (n)).
The connectNodes method joins both a single node and a subtree. Moreover, the binding occurs using comparison. Thus, the smallest element is always at the top of the tree. ConnectNodes
method :
private Node connectNodes(Node parent, Node node) {
if (node == null) {
return parent;
}
if (parent == null) {
return node;
} else {
if (compare(node, parent) < 0) {
return connectNodes(node, parent);
}
Node cur = parent;
Node n = node;
while (cur != null) {
if (cur.left == null) {
cur.left = n;
n.parent = cur;
cur.k++;
break;
}
if (cur.right == null) {
if (compare(n, cur.left) <= 0) {
cur.right = cur.left;
cur.left = n;
n.parent = cur;
cur.k++;
break;
} else {
cur.right = n;
n.parent = cur;
cur.k++;
break;
}
}
if (compare(n, cur.left) <= 0) {
Node tmp = cur.left;
cur.left = n;
n.parent = cur;
cur.k++;
cur = n;
n = tmp;
continue;
}
if (compare(n, cur.right) < 0
&& compare(n, cur.left) > 0) {
cur.k++;
if (cur.right.k < cur.left.k) {
Node tmp = cur.right;
cur.right = n;
n.parent = cur;
cur = n;
n = tmp;
} else {
cur = cur.left;
}
continue;
}
if (compare(n, cur.left) > 0) {
cur.k++;
cur = cur.left.k < cur.right.k ? cur.left : cur.right;
}
}
return parent;
}The connectNodes method should be given special attention. Adding a new element is performed using this method with respect to the root and the new element. We believe that the tree is not empty:

4 cases are possible:
- the new element is less than the root;
- The new item is smaller than the left child.
- the new element is larger than the left child, but smaller than the right;
- the new item is larger than the right child.
Case 1.
In this situation, the parent becomes the left descendant of the new element, if parent is the root of the tree, then the new, added element will be the new root, respectively.

Case 2.
There are two possible options: the right child is defined and the right child is not defined. If the left descendant is not defined, then we consider that the left descendant is of greater importance to the new node. In both situations, the new element becomes the left child of the parent, and left (which was the left child before adding) becomes the right child. However, in the second case, you need to join the old right descendant right to the new right descendant left. Joining left to right will occur according to the same rules as in the described cases.

Case 3
In this case, either the left subtree is jumped and a new node is added to it if there are fewer nodes than the right subtree, or the right subtree right is replaced with the inserted node node and the right subtree right is added to it.

Case 4.
In this case, the transition is performed along the subtree in which there are the least nodes. The number of nodes accumulates in the field k.

Now we estimate the asymptotic behavior of the connectNodes method . In the best case, when nodes without descendants are added to the tree in decreasing order, the asymptotic behavior will be O (1), since in this case, put the new element in the place of the grandparent. If we are talking about associating a node with descendants and smaller than the progenitor, then you will need to go through the subtree of the node. For case 2 in paragraph a)the asymptotics is O (1), and in step b) you need to again go through the subtree of the inserted node.
Note that the field k at the nodes increases for all cases except the 1st, this is done so that the tree is filled symmetrically, but without violating the increasing order of the left subtree if one occurs.
To assess the complexity of the passage through the tree, it is enough to evaluate its height. The height of the tree will be the desired asymptotic behavior. A separate issue is the presence of the length of the sequence on the left subtree. If we take into account the presence of such subtrees, in the worst case, the asymptotic behavior of the binding can be considered as the asymptotic behavior of the binding with the subtree that we want to bind, and in the best case, as O (1) (2 case).

Since when connecting nodes we are dealing with nodes inside the tree, the height of any subtree can be considered not to exceed the height of the tree itself. Thus, having estimated the height of the entire binary tree, we obtain the asymptotic behavior of the connectNodes method. Due to the fact that the selection of the subtree for insertion is selected based on the field k of the node (which stores the size of the subtree except for consecutively increasing increasing nodes, they are considered as one node), the tree tends to fill its next level only after filling the previous one (except, of course, described above case 1). Thus, the tree will have the form:

Thus, if n is the number of nodes in the tree, then
An element can be searched not in a tree, but in an array based on a hash code; therefore, the search operation has the asymptotics O (1). And since the tree is organized as a binary one, the root always contains the minimum element in comparison and the asymptotic behavior of the minimum search is O (1). I note that the removal of the minimum element has the asymptotics O (log (n)), since when deleting it is required to reorganize the tree, starting from the root using the connectNodes method .
At first glance, the operation to delete the minimum element in the implemented collection has worse asymptotics than the HashSet collection, but do not forget that before you remove the minimum element, you first need to find it, and for this you need to perform operations with the asymptotics O (n). Thus, the final asymptotic behavior of the operation to remove the minimum element in the HashSet collection will have the form - O (n).
Checking for the presence of an element in the collection, as mentioned above, is carried out on the basis of checking for null the element of the array at the index determined by the hash code of the element. The verification is performed by the contains method and has the asymptotic behavior of O (1):
public boolean contains(E element) {
int index = getElementHash(element);
return nodes[index] != null;
} Also, based on the hash code, a search is performed for equality with what with the same asymptotics using the getElement method :
public E getElement(E element) {
return (E) nodes[getElementHash(element)].data;
}The implemented collection is not without flaws. It requires more memory, it needs a hash function without collisions, and to implement enumeration of elements it is necessary to implement a tree traversal, which is also not a pleasure, but this collection is intended for other purposes. The main advantage is the ability to search for elements of the same type according to different criteria with the best asymptotics. As applied to my task, it was a search for equality based on coordinates and a search for a minimal element based on a comparison of the values of a metric function.
In the end, I’ll give the results of testing the collection for performance compared to the LinkedHashMap , TreeSet, and HashSet collections . All collections were filled with 1000 values of type Integer and, with filled collections, the following set of operations was carried out:
- placing a new item in the collection;
- checking for the presence in the collection of an element with a given value (the check was performed twice for an element that was in the collection and for an element that was not in the collection);
- search and removal is minimal by comparing an element;
- deletion of the item added in paragraph 1.
The test results are shown in the table:
| Collection | Number of repetitions | Time spent |
|---|---|---|
| LinkedHashMap | 10,000,000 | 1985 ± 90 ms |
| Treeset | 10,000,000 | 1190 ± 25 ms |
| Hashset | 1,000,000 | 4350 ± 100 ms |
| Hashtree | 10,000,000 | 935 ± 25 ms |
As a result, we have more than 2 times higher speed of the HashTree collection compared to LinkedHashMap and 1.27 times faster compared to TreeSet ( it makes no sense to consider a HashSet at all). Checks were performed on a machine with 4GB of RAM and an AMD Phenom (tm) II X4 940 processor, OS - 32-bit Windows7 Professional.
