Merge sort

Merge sorting work according to this principle:
- Looking for (as an option - formed) ordered subarrays.
- Ordered subarrays are connected into a general ordered subarray.
By itself, any ordered sub-array within an array has no special value. But if in the array we find two ordered subarrays, then this is a completely different matter. The fact is that very quickly and with minimal cost it is possible to merge over them - to form a common ordered subarray from a pair of ordered subarrays.

As you can see, it is very simple to combine two ordered arrays into one. It is necessary to move simultaneously in both arrays from left to right and compare the next pairs of elements from both arrays. The smaller element is sent to the common boiler. When the elements end in one of the arrays, the remaining elements from the other array are simply transferred in order to the main list.
This is the salt of the algorithms of this class. Initially, a random array can be broken up into many small ordered subarrays. During pairwise merging, the number of ordered subarrays decreases, the length of each of them increases. In the last step, the array is just two ordered subarrays, which merge into a single ordered structure.

The author of this concept is John von Neumann. Sometimes there is a controversial statement that he came up with sorting while working on the Manhattan project, as he was faced with the task of ensuring effective calculations of a huge amount of statistical data when developing a nuclear bomb. It is difficult to assess the plausibility of this version, since its first work on sorting by merger dates back to 1948, and the creation of the bomb was completed 3 years earlier. However, what is there for atomic sorting, let's take a look at it.
Natural Neumann merger
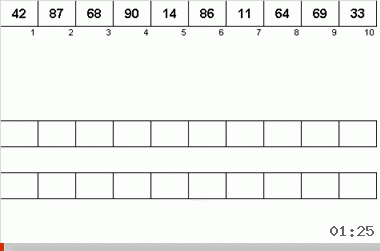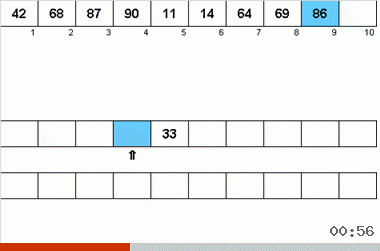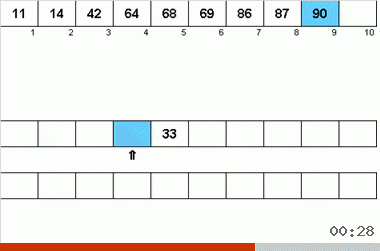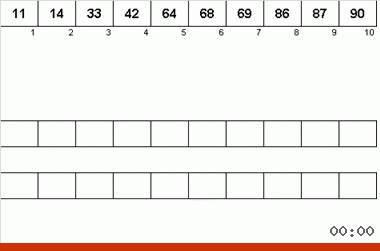
The Neumann algorithm was influenced by the design features of computers from the 40s. It looked like this:
- A total of three magnetic tapes are used — the main one on which unsorted data is recorded and two auxiliary ones.
- Data is sequentially read from the main tape.
- While the sequentially readable data is an ordered subarray, they are written to one of the auxiliary tapes.
- As soon as the next sorted subarray is completed (i.e., an element smaller than the previous one is found on the main tape), a pointer is put on the auxiliary tape (the end of the subarray) and a switch to another auxiliary tape occurs.
- Items 2-4 are repeated again, only the data is transferred to another auxiliary tape. At the completion of the next ordered sub-array on the main tape, alternately switching to one auxiliary tape, then to another takes place.
- When all data from the main tape is read, the processing of auxiliary tapes takes place.
- Data is read from both auxiliary tapes.
- In this case, the next data from the two tapes are compared with each other. According to the results of the comparison, a smaller element from the pair is recorded on the main tape.
- Since the borders of the arrays on the auxiliary tapes are marked with pointers, reading and comparison occurs only within the sorted subarrays.
- If on one of the auxiliary tapes the elements of the next sub-array have run out, then from the remaining tape the remainder of the sub-array is simply transferred to the main tape.
- Repeat the whole process again until the data on the main tape is a completely ordered array.
The Neumann sorting is an adaptive algorithm: it not only fixes the sorted pieces of the array, but first of all tries to increase them in order to form even longer ordered subarrays on the basis of the elongated ordered subarrays. Therefore, it is also called adaptive merge sorting .
The complexity of this algorithm is modest - O ( n 2 ), and, nevertheless, for the pioneers of tube calculations, this was a breakthrough.
On the example of this first merge sorting, the lack of this class of algorithms is already visible - the cost of additional memory. In this regard, almost all merge sorting additionally requires O ( n ), but occasionally there are elegant exceptions.
Bose-Nelson Direct Merger
Strictly speaking, the Bose-Nelson algorithm is a sorting network, not a sorting network. In the process, the array and all its subarrays are divided in half, and nothing prevents all these halves from being processed in parallel at all stages. However, it can be presented in the form of sorting. And we will sometime get to the topic of sorting nets too.

- The array is divided in half - on the left and right halves.
- Elements are divided into groups.
- In the first iteration, these are two elements (the 1st element of the left half + the 1st element of the right half, the 2nd element of the left half + the 2nd element of the right half, etc.), on the second iteration - the fours of elements (1 the 2nd and 2nd elements of the left half + the 1st and 2nd elements of the right half, the 3rd and 4th elements of the left half + the 3rd and 4th elements of the right half, etc.), on the third - eights, etc.
- Elements of each group from the left half are a sorted subarray, elements of each group from the right half are also a sorted subarray.
- We merge the sorted subarrays from the previous item.
- We return to point 1. The cycle continues until the size of the groups is less than the size of the array.
It may seem that additional memory is required here. But no! For a clearer perception in animation, the left and right halves of the array are located on top of each other, so that the relative position of the compared subarrays is more obvious. However, due to strict division in half, an algorithm is possible, in which all comparisons and exchanges are made on the spot, without attracting additional memory resources. Which is very unusual for merge sorting.
defbose_nelson(data):
m = 1while m < len(data):
j = 0while j + m < len(data):
bose_nelson_merge(j, m, m)
j = j + m + m
m = m + m
return data
defbose_nelson_merge(j, r, m):if j + r < len(data):
if m == 1:
if data[j] > data[j + r]:
data[j], data[j + r] = data[j + r], data[j]
else:
m = m // 2
bose_nelson_merge(j, r, m)
if j + r + m < len(data):
bose_nelson_merge(j + m, r, m)
bose_nelson_merge(j + m, r - m, m)
return dataThere is still in all the sorts of merge something that makes them related to the hydrogen bomb. First there is a division, then synthesis.
Links
Articles series:
- Excel application AlgoLab.xlsm
- Exchange sorting
- Sorting inserts
- Sort by selection
- Merge sort
- Balanced merger top-down and bottom-up
- Multiphase merge sorting
- Cascade Merge Sort
- Oscillating merge sort
- Filamentous and immiscible sorting
- Merge sort comparison
Both of the sortings mentioned in today's article are now available in the AlgoLab application (who studies the algorithms using this Excel application, update the file). And in just a couple of days, with the release of a quick continuation on merge sorting, several more algorithms of this class will be available.
For the Bose-Nelson sort, a limit is set - the size of the array must be a power of two. If this condition is not met, the macro will cut the array to the appropriate size.
The article was written with the support of the company EDISON Software, which writes software for 3d-reconstruction and is engaged in the development of sophisticated measuring equipment .

